Лекция 8
.docПример построения регрессионной модели
Однофакторная
линейная модель имеет вид:
.
1). Для нахождения
коэффициентов
и
применим метод наименьших квадратов:
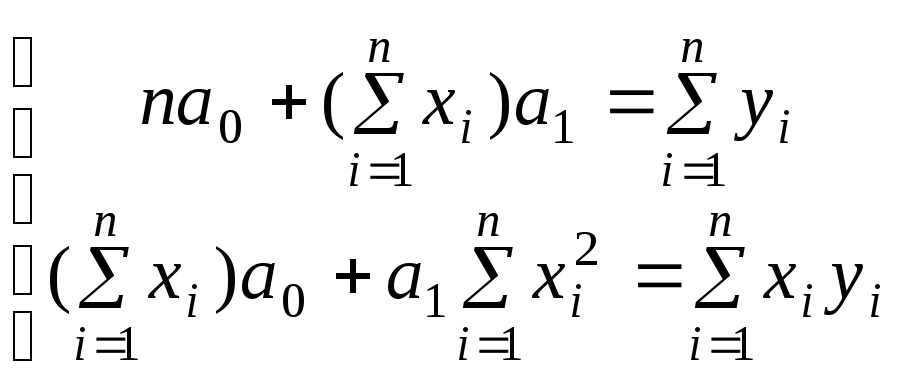(1)
где n – число опытов;
- факторный признак;
- результативный
признак.
Если после решения
системы (1), коэффициент
,
то связь между х
и у является
прямой.
2). Теснота этой связи определяется коэффициентов корреляции:
.
(2)
Коэффициент корреляции находится в интервале от 0 до 1. Чем ближе коэффициент корреляции к единице, тем теснее связь между результативным и факторным признаками.
Средняя квадратическая ошибка выборки:
,
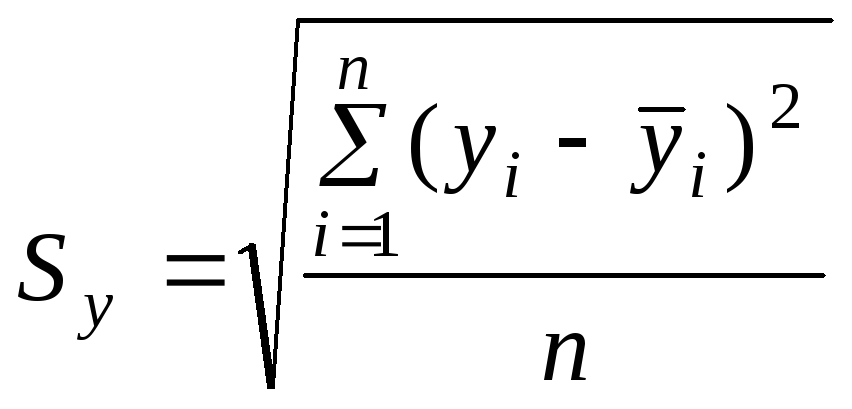(3)
где
-
среднее арифметическое значение.
Рассчитывается по формуле:
.
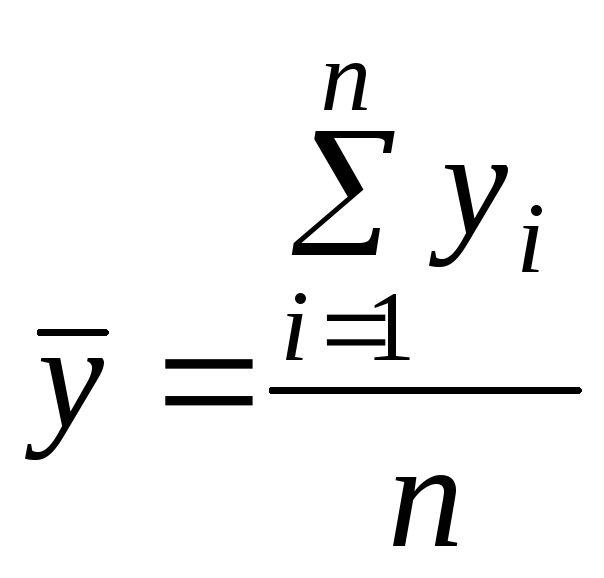(4)
Средняя квадратическая ошибка уравнения регрессии:
.
(5)
3). Коэффициент
детерминации показывает долю изменения
результативного признака под воздействием
факторного признака:
.
4). Коэффициент эластичности показывает, на сколько процентов изменятся результативный признак при изменении факторного признака на 1%. Коэффициент эластичности рассчитывается по формуле:
,
(6)
где
- среднее арифметическое значение
факторного признака,
-
среднее арифметическое значение
результативного признака.
5). Бетта - коэффициент показывает, на сколько изменится результативный признак, если изменится факторный:
,
(7)
где
,
- средние квадратические ошибки выборки.
6). Средняя по модулю относительная ошибка аппроксимации:
.
(8)
7). Среднее квадратическое отклонение:
,
где к
– количество признаков.
(9)
Этапы построения регрессионной модели
Описание
Регрессией в теории вероятностей и математической статистике принято называть зависимость среднего значения какой-либо величины y от некоторой другой величины или от нескольких величин хi.
Парной регрессией называется модель, выражающая зависимость среднего значения зависимой переменной y от одной независимой переменной х:
y=f(x)+ε,
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак–фактор).
Парная регрессия применяется, если имеется доминирующий фактор, обуславливающий большую долю изменения изучаемой объясняемой переменной, который и используется в качестве объясняющей переменной.
Множественной регрессией называют модель, выражающую зависимость среднего значения зависимой переменной y от нескольких независимых переменных х1,х2,…,хp, т.е.:
y=f(x1,x2,...,xp).
Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать одновременное влияние нескольких факторов.
Этапы построения регрессионной модели
-
Анализ исходных данных. На этом этапе рассчитываем выборочные характеристики
-
среднее арифметическое M(X)
-
дисперсия D(X)
-
cтандартное отклонение σ2
-
выполняется отбор факторов для множественной регрессии:
-
Факторы не должны быть взаимно коррелированы и, тем более, находиться в точной функциональной связи. Наличие высокой степени коррелированности между факторами может привести к неустойчивости и ненадежности оценок коэффициентов регрессии, а также к невозможности выделить изолированное влияние факторов на результативный показатель.
-
Включение фактора в модель должно приводить к существенному увеличению доли объясненной части в общей вариации зависимой переменной. Формальная проверка существенности вклада фактора в модель выполняется с помощью оценки значимости соответствующего частного коэффициента корреляции либо значимости коэффициента в уравнении регрессии.
-
Постановка задачи. Предположим, что значение каждого отклика yi как бы состоит из двух частей:
-
закономерный результат того, что фактор х принял конкретное значение хi
-
некоторая случайная компонента εi, которая никак не зависит от значения хi. Таким образом, для любого i=1…n существует функция yi=f(xi)+εi. Смысл случайной величины (ошибки) ε:
-
внутренне присущая отклику у изменчивость
-
влияние прочих, не учитываемых в модели факторов
-
ошибка в измерениях
-
Предположения о характере регрессионной функции.. Методы подбора вида функции: графический и аналитический. Возможный вид функции f(xi):
-
линейная: y=b0+bx
-
полиномиальная: y=a0+a1x+a2X2…anxn
-
степенная: y=axb
-
экспоненциальная: y=aex
-
логистическая: y=K1+aebx
Оценка параметров линейной регрессионной модели. Сделать можно например методом наименьших квадратов. Экономическая интерпретация коэффициентов:
-
a – «постоянная составляющая» отклика, независимая от фактора
-
b – степень влияния фактора на отклик (случаи отрицательного)
Исследование регрессионной модели.
-
Теснота связи между фактором и откликом. Для этой цели служит коэффициент корреляции r_{xy, rxy∈[−1,1]. Отрицательное значение rxy означает, что увеличение фактора приводит к уменьшению отклика и наоборот.
-
Доля вариации отклика y, объясненная полученным уравнением регрессии характеризуется коэффициентом детерминации R2,R2∈[0,1].
Проверка статистической значимости уравнения регрессии.. На этом этапе производится оценка достаточно ли велик R2, чтобы говорить о существовании значимой связи между величинами x и y. Для этого расчитывается значение F-критерия Фишера. В качестве нулевой гипотезы H0 берется предположение о равенстве 0 всех коэффициентов регрессии. Если F>F∗крит^, то H0 отвергается, иначе принимается. F∗крит^ берется из таблиц для заданного уровня значимости.
Характеристика оценок коэффициентов уравнения регрессии. Вычисляем стандартные ошибки - это оценка среднеквадратического отклонения дисперсии случайной величины от ее истинного значения: sb=∑e2i(n−1)∑(xi−x¯)−−−−−−−√. Сравнивая значение коэффициента с его стандартной ошибкой sb, можно судить о значимости коэффициента. Коэффициент называется значимым, если есть достаточно высокая вероятность того, что его истинное значение отлично от нуля. Для стандартных ошибок нет таблиц критических уровней, поэтому используется t-статистика.
Построение доверительных интервалов. На этом этапе строится интервал, в который попадет значение с заданной вероятностью.
Проверка статистической значимости коэффициентов регрессии. В качестве H0 берется предположение, что коэффициент равен 0. Для ее проверки расчитывается t-статистика: tb=bsb. Если |t|<tγ(n−1) – гипотеза Н0 не отвергается, т.е. выбранная переменная никакого влияния на отклик не оказывает, соответственно переменная не значима
Оценка параметров множественной регрессии
-
Несмещенность - математическое ожидание остатков равно 0
-
Состоятельность - увеличение точности оценок с увеличением выборки
-
Эффективность - оценки характеризуются наименьшей дисперсией.
Исследование осатков. Пердпологает проверку 5 пердпосылок МНК:
-
случайный характер остатков
-
нулевая средняя величина остатков, не зависящая от xi
-
Гомоскедастичность - дисперсия каждого отклонения εi одинакова для всех значений x, Проверить ее можно с помощью тестов Голдфелда – Куандта, Глейзера
-
отсутствие автокорреляции остатков. Значения остатков распределены независимо друг от друга. Для обноружения используются тесты: Дарбина-Уотсона,Бройша — Годфри. Возможные причины:
-
неверно выбрана функция регрессии
-
имеется неучтенная объясняющая переменная (переменные)
осатки подчиняются нормальному распределению
При выполнении 5 предпосылок выше оценки полученные по МНК и по медоту максимального правдоподобия (ММП), совпадают между собой. Для применения ММП необходимо знание формы закона распределения исследуемой случайной величины. На вход подается некоторая величина x, а на выходе имеется величина y. Также существует условная вероятность p0(y|x) описывающая вероятность получить на выходе величину y, если на вход была подана величина x. Если множество величин не дискретно (их значения не образуют конечное или счётное множество), то условная вероятность заменяется на условную плотность распределения.