Матрицы чувствительности

Полезность любого информационного источника определяется тем, какое влияние каждый из его выходов оказывает на меру уверенности целевой гипотезы. Пусть Т — переменная, соответствующая целевой гипотезе, и пусть X — тестовая переменная, т.е. наблюдаемый узел, воздействие которого на Т необходимо уточнить. Если текущая уверенность в Т определяется соотношением BEL(t) = P(t/e), тогда апостериорная уверенность BEL(t/x) = P(t/e,x) будет указывать, насколько чувствительна величина BEL(t) по отношению к каждому значению переменной, которое х может принять. Мы, следователь­но, определяем матрицу чувствительности of T по отношению к х матрицей

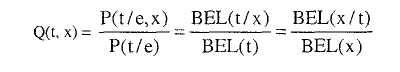
Заметьте, что Q(t, x) — динамическая функция, высоко чувствительная к текущему свидетельству е, и симметричная, т.е.

Матрица чувствительности Q(t, x) может служить для определения приоритетов активностей.

4.4. Стратегии, основанные на теории полезности

ЛПР стремится к максимизации ожидаемой полезности Другими словами, из всех возможных решений он выберет то, которое обеспечивает наи­большую ожидаемую полезность Полезность — это некоторое число, при­писываемое лицом, принимающим решение, каждому возможному исходу. У каждого ЛПР своя функция полезности, которая показывает его предпоч­тения к тем или иным исходам в зависимости от его отношения к риску.

Выбор между вариантами действий основывается на оценках выигрыша, прибыли или цены или желательности. Каждое из различных последствий взвешивается с учетом вероятностей. Последствия, связанные с оценкой потерь называются платежами или ценами. Таким образом, рациональная теория выбора может быть представлена с помощью пар:

L = (С,Р), где С = {С₁, С₂, … С_n} есть конечное множество цен последствий и Р — распределение вероятностей на С, удовлетворяющее условию:

Каждая пара L = (С,Р) называется лотереей и может быть представлена либо списком пар L = [С₁, Р(С₁); С₂, Р(С₂); ., . .,; С_n, Р(С_n)], либо древовид­ной диаграммой.

Представим теперь, что байесовская сеть находится в равновесии. Мера уверенности приписана всем вершинам в сети, и мы хотим оценить чувстви­тельность Т в некоторой вершине х. s(t,x) — может быть вычислена двумя способами. Во-первых, прямой способ инстанциировать узел X (временно) каждым из его значений, распространить воздействие каждой инстанциации Х=х по отношению к Т, вычислить результирующие значения BEL(t/x) и поделить на предыдущие значения BEL(t). Во-вторых, существует косвенный или широковещательный способ: инстанциировать Т (временно) каж­дым из его значений, распространить влияние каждой инстанции Т = t по направлению к X, вычислить результирующую веру BEL(t/x), и поделить предыдущее значение уверенности BEL(x). BEL(t) — доступно в Т до инстанциации, в то время как BEL(x) — доступно в х до распространения.

Аксиомы теории полезности

Аксиомы теории полезности подытоживают принятие свойства стратегий, которыми обычно пользуются люди.

Аксиома 1. Упорядоченность

Между ценами (выигрышами) любой лотереи должно существовать линейное и транзитивное отношение предпочтения. Будем обозначать это отношение .

Аксиома 2. Непрерывность

Если С₁ * С₂ * С₃ тогда существует лотерея L только с двумя выигрышами, которая эквивалентна получению С₂, т.е .

Вероятность р, при которой достигается эквивалентность, может быть использована, чтобы калибровать С₂ по отношению к выигрышам С₁, С₃.

Аксиома 3. Замещаемостъ.

Для любого 0 < р 1 и любой из трех лотерейL₁, L₂, L₃, L₁ ~ L₂ если и только если

Аксиома 3 утверждает, что добавление того же самого приза (L₃) с той же самой вероятностью (1-р) к двум эквивалентным лотереям не изменит предпочтения между ними

Аксиома 4. Монотонность

При сравнении двух лотерей, каждая из которых с тем же самым призом, лотерея, дающая больший выигрыш с более высокой вероятностью, является более предпочтительной, т. е, если

тогда

если и только если р р^,.

Аксиома 5. Редукция составной лотереи

Предпочтения определяются исключительно на основе финальных исходов и связанных с ними вероятностей, но не в том виде, как они представле­ны, т.е для любых двух лотерей L₁ и L₂ = [q,C₁, (1-q), C₂], [p,L₁; (1-p), L₂] ~ [p,L₁;(l-p)q,C₁;(l-p)(l-q),C₂].

Другими словами, составная лотерея [p,L₁; (1-p), L₂] в качестве выигрыша может быть редуцирована к эквивалентной лотерее, которая пере­числяет эксплицитно выигрыши L₂, С₁ и С₂, связанные с ними вероятностя­ми. Эта аксиома иногда называется «в играх не бывает фантов», поскольку она не придает никакого значения числу шагов, необходимых для того, что­бы достичь успеха.

Теорема 1. Если совокупность предпочтений в лотерее удовлетворяет ак­сиомам 1-5, тогда существует вещественнозначная функция U на множестве платежей (призов) С и правило распространения функции на множество лотерей такое, что для любых двух лотерей L₁ и L₂, L₁ L₂, если и только если

Другими словами, каждый вид совокупности предпочтений, удовлетворяющий аксиомам 1-5 может быть безболезненно закодирован определением меры полезности каждого отдельного следствия и принятия решения обо всех предпочтениях между лотереями на основе функции ожидаемой полез­ности. Альтернативой является стратегия, которая выбирает всегда лотерею с наивысшей ожидаемой полезностью, гарантирует выбор, который совмес­тен с аксиомами 1-5, независимо от полезности, приписанной следствием.

Мера ценности взаимной информации.

Взаимная информация — одна из наиболее широко используемых мер для ранжирования информационных источников. Она основана на предположении, что неопределенность, относящаяся к любой переменной z, характеризуется распределением вероятностей P(z) и может быть представлена функцией энтропии

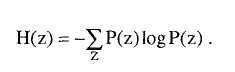
Соответственно, двойственным образом значение истинности целевой переменной Т, при условии, что X инстанциирована х, может быть записано в виде:

и средняя взаимная неопределенность Т, просуммированная по всем возможным исходам х равна:

Если мы вычтем H(t/x) из исходной неопределенности Т до оценки X, а именно Н(Т), мы можем получить полный потенциал X по уменьшению неопределенности. Этот потенциал называется взаимной информацией Шеннона и определяется

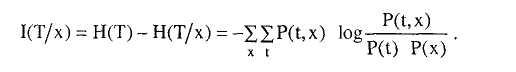
Полезность чаще всего связывают с ожидаемой денежной оценкой. Если ЛПР безразлично к риску, то оно принимает решение на основании полезности, оцениваемой как величина, пропорциональная ожидаемой оценке по­лезности. Учитывая, что U — индивидуальное число, характеризующее ЛПР, функцию полезности можно представить в виде функции U(v), где v — прибыль, получаемая при различных исходах, является прямой с положи­тельным наклоном.

Для принятия решения в случае небезразличия ЛПР к риску, необходи­мо уметь оценивать значения полезности каждого из допустимых исходов. Дж. Нейман и О. Моргенштерн предложили процедуру построения инди­видуальной функции полезности, которая заключается в следующем: ЛПР отвечает на ряд вопросов, высказывая свои индивидуальные предпочтения и отношение к риску. Значения полезностей могут быть найдены за два шага.

Шаг 1. Присваиваются произвольные значения полезности выигрышам для наихудшего и наилучшего исходов (например, 0 и 50), причем первой величине (худший исход) ставится в соответствие меньшее число. Тогда полезности промежуточных выигрышей будут находиться в интервале 0— 50. Полезность исхода даже для одного индивида определяется не однозначно, а с точностью до монотонного преобразования. Пусть например, имеем х₁,х₂,...х_n — полезности, приписываемые n ожидаемым значениям выигрышей, тогда а + bх₁, а + bх₂, ..., а + bx_n, где b>0, также будут полезностями.

Шаг 2. ЛПР предлагается на выбор: получить некоторую гарантирован­ную денежную сумму v, находящуюся между лучшим и худшим значениями S и s, либо принять участие в игре, т.е., получить с вероятностью р наиболь­шую денежную сумму S, и с вероятностью (1-р) — наименьшую сумму s. При этом вероятности следует изменять (понижать или повышать) до тех пор, пока ЛПР станет безразличным по отношению к выбору между получе­нием гарантированной суммы и игрой. Пусть указанное значение вероятно­сти равно р_о, полезность гарантированной суммы определяется как среднее значение (математическое ожидание) полезностей наименьшей и наиболь­шей сумм, т.е.

Таким образом, если определена шкала измерения, то может быть по­строена функция полезности ЛПР.

В общем случае график функции полезности может быть трех типов (рис. 4.11. а, b,с).

Склонность или несклонность ЛПР к риску зависит от его финансового положения, текущей ситуации принятия решения и других факторов. Иначе говоря, эта характеристика не является абсолютной, присущей ему при лю­бых обстоятельствах.

Рис 4.11 Типы функции полезности (а - ЛПР не склонно к риску, b—ЛПР безразлично к риску, с — ППР склонно к риску)