4.3. Стоимость и ценность информации

Считается общепринятым, что информация является полезным товаром, действующим таким образом, что действия информированного агента бо­лее предпочтительны, чем действия агента в отсутствии информации. Вот почему люди аккумулируют информацию, когда она доступна и покупают информацию, когда она продается. Предельная цена информации — цена, которую можно было бы заплатить за идеально полную информацию, если бы таковую удалось получить. Имея ее, можно было бы принимать без­ошибочные решения. Она представляет собою разность между платежом, который можно было бы получить при наличии идеальной информации, и выплатой, которую дает реально имеющаяся информация. Понятию «ценность информации» может быть придан точный смысл. Ценность любого информационного источника определяется как разность между полезностями двух оптимальных стратегий, одна из которых обеспечивает свободу выбора различных действий для исходов (платежей), связанных с исполь­зованием информации и вторая в отсутствии такой свободы. Этот критерий может быть использован, чтобы ранжировать полезность различных ин­формационных источников и решить, нужно ли приобретать очередную порцию информации. Целесообразность запроса значения переменной X может быть оценена до ее фактического наблюдения при следующих условиях: если мы запрашиваем X и находим, что значение есть х, полезность действия d будет равна

где U(s) — мера полезности состояния s, P(s/d, e, X = х) — распределение вероятностей перехода в состояние s при условии выбора решения d и дан­ных наблюдения е.

На данном этапе мы можем выбрать наилучший вариант среди всех альтернатив и получить ценность (значение = value)

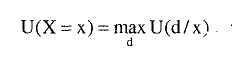
Однако поскольку нам не известно фактическое значение запрашиваемой переменной х, мы должны усреднить полезность U(X=x) по всем возможным значениям х, взвешенным по их вероятностям. Таким образом, полезность запроса X равна

где е — свидетельства, собранные до того, как мы запросили значение х. Пример 1 помогает проиллюстрировать этот анализ. Оцениваемые источни­ки являются двумя возможными экспертизами, и запрашиваемые перемен­ные являются исходами этих экспертиз. На рис. 4.9 показано дерево реше­ний с вероятностями на дугах и метками полезности в вершинах. Ветви по­мечены как t₁ и t₂. Жирными линиями выделен оптимальный план. Ветви, помеченные буквами t₁ и t₂, представляют варианты решений о том, чтобы выполнить экспертизу, в то время как ветвь t_o представляет решение воздер­жаться от использования какой бы то ни было экспертизы. Метки полезно­сти на этих ветвях показывают, что экспертиза t₁ имеет ценность не менее 13 ед., поскольку после проведения экспертизы полезность вершины увели­чилась до 303 ед., т.е. на 303 - 290 = 13 ед. по сравнению со случаем, когда экспертиза не производилась даже после того, как за проведение экспертизы произведена оплата в размере 50 ед. Из рисунка видно, что экспертиза t₂ имеет нулевую ценность, во-первых, потому, что полученная полезность 270 ед. меньше, чем полезность 290 ед., которая имеет место в случае отсутствия всякой экспертизы; во-вторых, полезность решения как в случае положи­тельного заключения экспертизы, так и в случае отрицательного остается неизменной и равной 270 ед., что меньше на 290 ед. в случае отсутствия экс­пертизы.

Источник характеризуется функцией условной вероятностиP(x/z), где х — есть выход источника и Z, множество всех переменных, которые влия­ют на

полезность последствий.

Рис. 4.9. Выбор оптимального варианта инвестиций

Источнику может быть приписана ценность, когда мы имеем полную информацию, необходимую для вычисления ожидаемой полезности U(d/z) для каждого доступного действия d. Заметьте, однако, что если доступны несколько информационных источников и их можно опрашивать в произвольном порядке, понятие ценности информации сводится к локальной характе­ристике каждого источника, другими словами, имеет место независимости источников информации. В принципе, определение полезности информации с позиции теории решений помогает составлять расписание работы с источ­никами информации в информационных системах Например, оно может быть использовано для принятия решения, какой следующий вопрос задать пользователю, какой тест провести следующим, какое правило использовать следующим в экспертной системе, какой узел сети вывода активизировать следующим. Однако прежде чем оценить источник информации, пользователю необходимо вынести суждение обо всех других источниках, их последствиях, их полезностях Обычно нам предлагают выбрать один из конкури­рующих источников до получения детального знания, необходимого для их оценки и до полного решения проблемы упорядочения источников по цен­ности С этой целью мы должны ранжировать источники в порядке убыва­ния их ценности

Чтобы получить практические рекомендации для выбора из информационных источников, мы должны сделать некоторые упрощения Наиболее популярными являются следующие упрощения

Отсутствие конкуренции Каждый информационный источник оценивается по отдельности так, как если бы существовал только один единственный источник, доступный для принятия решения Это предположение приводит нас к одношаговой политике (рис 4 10)

Рис. 4.10. Структура дерева выбора оптимальных

информационных источников

На рис 4 10 показано четырехуровневое дерево. Первый уровень отражает решение нужно ли обращаться к информационному источнику и дейст­вовать без него, второй уровень отражает потенциальные ответы, которые будут выданы информационным источником, третий уровень отражает вы­бор (d), который должен сделать ЛПР, а четвертый уровень отражает со­стояние объекта.

Полезность источника обозначается U(x) и определяется как

Это дает полезность U_i для информированного выбора

что отражает как вероятность получения значения х, так и полезность оптимального действия после этого. Условная вероятность P(x/s) полностью ха­рактеризует природу информационного источника в той части, насколько достоверно х отражает s. Нижний путь, помеченный U_o, отражает полезность, которую ЛПР ожидает получить, когда действует в отсутствие информации, т. е. без консультации с информационным источником. Ценность информационного источника V() для ЛПР есть разница между верхним инижним путем

Эта разность всегда неотрицательна, т. е. V()0, говорит о том, что ЛПРникогда не проиграет от приобретения дополнительной информации, потому что у него всегда имеется возможность игнорирования приобретенной информации и применения действий, которые оптимизируют нижнюю границу

Пример 2. Предположим, что значение х открывает истинное состояние объекта s, т. е. P(x/s) = P(s/x) = , где— матрица идентичности.

Подставляя в (2) мы получаем

где d° — оптимальное действие без учета полученной информации. Результаты подстановки значений параметров представлены в таблице 4. 1.

Таблица 4.1

Не зная s, лучшее, что мы можем сделать - выбрать действие d⁰ = d₁ для всех состояний, давая полезность U_o

При наличии совершенной информации мы получаем наивысшую полезность в каждой строке из-за того, что мы можем выбрать действие, которое лучше всего подходит под известное состояние объекта. Следовательно, по­лезность совершенной информации определяется

Пример 3. Предположим, мы имеем несовершенную информацию, и действие d заключается в том, чтобы угадать состояние объекта s. Полезность предполагается равной 1, если догадка является правильной и 0 — в противном случае, т.е. U(d, s) = _d,s. Подставляя в (2), получим

Вновь составим численный пример (табл. 4.2).

Таблица 4. 2