
- •Глава 4. Роль интеллектуальных
- •Процедура выбора при наличии многих критериев
- •Правила выбора
- •Выбор по парето
- •Лексикографический выбор
- •Мажоритарный выбор
- •4.2. Модель информационной системы поддержки принятия решений
- •4.3. Стоимость и ценность информации
- •Управление доступом к источникам посредством релевантности
- •Матрицы чувствительности
- •4.4. Стратегии, основанные на теории полезности
- •Аксиомы теории полезности
- •4.5. Имплементация и мониторинг стратегий
Лексикографический выбор
Сх(х) можно рассматривать как выбор по отношению к R\:
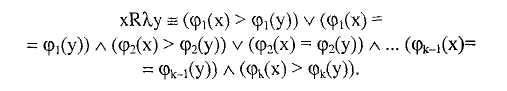
Выразим
условие
xR![]() Xy
через переменные Ui
и Vi:
Xy
через переменные Ui
и Vi:
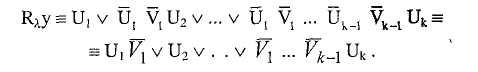
Это соотношение может быть переписано в виде:
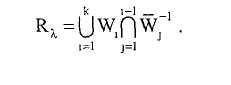
Мажоритарный выбор
С![]() (х)порождается
отношением R
(х)порождается
отношением R![]() ,
которое
с использованием булевых переменных
можно представить в виде:
,
которое
с использованием булевых переменных
можно представить в виде:
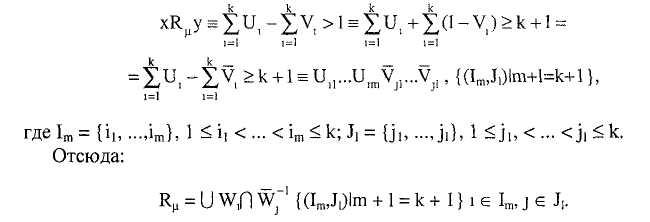
Оценку
варианта решения х,
по
критерию
φi,
i
= 1,
..., k
будем
называть аij
=
φj/хi).
Будем называть матрицу А матрицей
оценок; строку матрицы аi=(аi1,аi2,...,
аin)
—
векторной оценкой варианта xi.
Назовем
точку х
![]() G
полуэффективным
(слабооптимальным по Парето) решением
многокритериальной
задачи, если у
G
полуэффективным
(слабооптимальным по Парето) решением
многокритериальной
задачи, если у
![]() G,
φ(у) > φ(х), эффективным (оптимальным
по Парето)
решением многокритериальной задачи,
если y
G,
φ(у) > φ(х), эффективным (оптимальным
по Парето)
решением многокритериальной задачи,
если y
![]() G,
φ(у)
G,
φ(у)
![]() φ(х).
φ(х).
Идеальным
решением многокритериальной задачи,
если y
![]() G,
φ(х)
G,
φ(х)
![]() φ(у).
φ(у).
В
зависимости от постановки задачи,
элементы матрицы парных сравнений
aij
и
аji
должны
удовлетворять определенным соотношениям
нормировки. Если варианты равноценны,
будем обозначать их хi
~ хj
(а также если варианты
несравнимы). Если хi
![]() xj
то должно выполняться условие аij
> аji.
xj
то должно выполняться условие аij
> аji.
Рассмотрим возможные варианты нормировки.
1. Простая нормировка
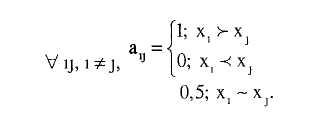
2. Турнирная нормировка
![]()
аij — число очков, C=const — число игр.
3. Кососгшметрическая нормировка
![]()
4. Вероятностная нормировка
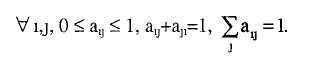
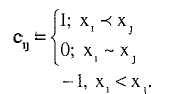 Сигнатурная
нормировка
Сигнатурная
нормировка
Как отмечалось выше, Парето-оптимальное решение в многокритериальной задаче выбора принимается в соответствии с правилом:
![]()
и![]() ли
в эквивалентной записи:
ли
в эквивалентной записи:
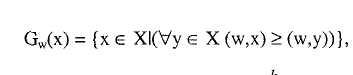
![]()
где (w,x) — скалярное произведение:
Функция выбора в этом случае определяется вариантами с максимальной взвешенной суммой критериев.
Пример. Примем, что число критериев не равно числу возможных вариантов. Рассмотрим в качестве примера три варианта выбора места работы (размещения средств, инвестиций, приобретения ценных бумаг). Предположим, что они различаются по критериям (рис. 4.5):
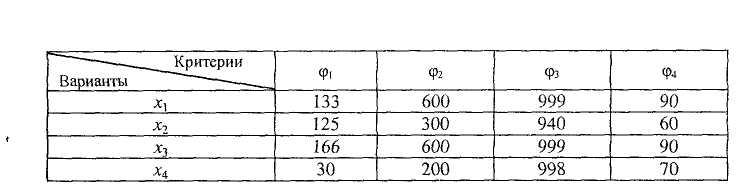
Рис.4.5. Матрицы критериев
Сформулируем матрицы Ск, к = 1, 2, 3, 4 попарного сравнения вариантов по критерию φк(х). В этой матрице элемент Сijk, ij=l, 2, 3 принимает значение + 1, если по критерию φк(х) вариант хi предпочтительнее варианта хj. Выполним нормировку критериев таким образом, чтобы выполнялось условие:
![]()
где к — номер критерия, i,j — номер варианта.
Т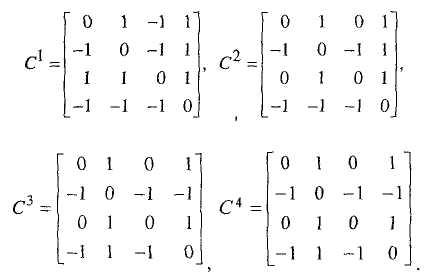 огда
для нашего примера мы получим следующие
четыре матрицы:
огда
для нашего примера мы получим следующие
четыре матрицы:
Рис.4.6. Матрицы предпочтительности вариантов
В трехзначной логике Лукасевича справедливы следующие таблицы истинности основных функций алгебры логики.
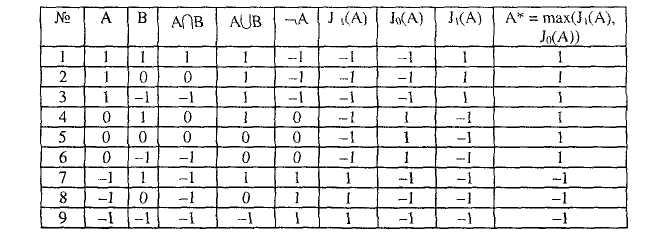
Рис 4.7. Таблица истинности логических функций
в трехзначной логике Лукасевича
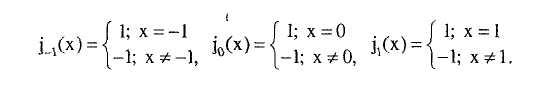 В
таблице обозначено:
В
таблице обозначено:
Рассмотрим выбор по к критериям φi, i=l,... ,k и обозначим Wi — отношение слабого порядка, отвечающее критерию φi.
Отношение слабого порядка R является интранзитивным, антисимметричным и антирефлексивным.
Зафиксируем
некоторую пару (х,у)
![]() и введем булевы переменныеUi,
Vi
(i
= 1, ..., к), причем Ui
= 1 = (х,у)
и введем булевы переменныеUi,
Vi
(i
= 1, ..., к), причем Ui
= 1 = (х,у)
![]() Wi,
Wi
— отношения слабого порядка.
Wi,
Wi
— отношения слабого порядка.
![]()
З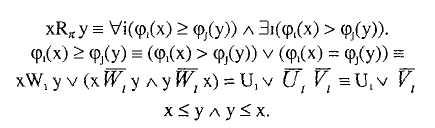 апишем
критерий выбора по Парето с использованием
булевых функций:
апишем
критерий выбора по Парето с использованием
булевых функций:
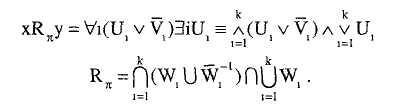 Отсюда
следует:
Отсюда
следует:
1.
Скалярный оптимизационный механизм —
выбор лучшего по заданному
скалярному критерию качества φ(х)
варианта х
![]() Х:
Х:
![]()
2. Условно-экстремальный механизм — выбор, определяемый схемой математического программирования с целевой функцией fo(x) и функционалами ограничений fi(x), i = 1,..., m:
![]()
3![]() .
Оптимизационный механизм доминирования,
определяемый бинарнымотношением
R:
.
Оптимизационный механизм доминирования,
определяемый бинарнымотношением
R:
4. Механизм блокировки: выбор неулучшаемых по R элементов х:
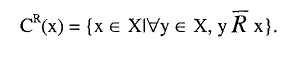
5.
Механизм ограничений, определяемый
бинарным отношением R
и заданным
элементом u
![]() G
выбора элементов х
G
выбора элементов х
![]() X,
лучших по R
фиксированного элемента u
X,
лучших по R
фиксированного элемента u
![]() G.
G.
![]()
С
использованием матриц Ck,
(к = 1, 2, 3, 4) и учитывая таблицу истинности
логических функций в трехзначной
логике, сформулируем отношение для
парето-оптимальных решений в виде
логической функции следующего
вида.
Rπ(xi,xj)=![]() или эквивалентно
R
я
(xi,
хj)=
= R
я
1(xi,
хj)
или эквивалентно
R
я
(xi,
хj)=
= R
я
1(xi,
хj)![]() (R
я
2(xi,
хj))
(R
я
2(xi,
хj))
Если
мы
примем
в качестве критерия R
я
= R
я
1![]() R
я
2,
где R
я
2
— условие
R
я
2,
где R
я
2
— условие
![]() ,
a
R
я
1—
логическое произведение матриц (Ск)*:
,
a
R
я
1—
логическое произведение матриц (Ск)*:

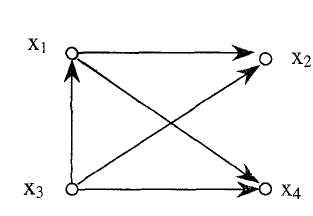
Таким образом, в данном случае парето-оптимальное решение составит множество пар элементов множества решений (х1, х4), (х3, x1), (х3, х2), (х3, х4), (х1, х2), т.е. тех пар множества решений, для которых соответствующие элементы матрицы R я равны 1. В виде графа это отношение можно представить следующим образом (рис. 4.8).
Рис. 4.8. Граф оптимальных
вариантов
Матрица R я 1 имеет единицы только в том случае, если для данной пары xi ни по одному из критериев не уступает хj. R я 2, как мы видели, содержит элемент rij2 = 1 в том и только в том случае, когда вариант хi превосходит вариант хj хотя бы по одному из критериев. Что означает фактически операция *? В результате выполнения операции у = z* над переменной z, у принимает значение 1, когда переменная z принимает значение 0 или 1, т.е. неотрицательное. С другой стороны, неотрицательность величины z есть следствие того, что либо вариант хi превосходит вариант хj по данному критерию, либо равноценен ему (во всяком случае, не уступает). Что же мы получим в результате логического и поэлементного умножения матриц Сij*? Каждый элемент результирующей матрицы в нашем случае:
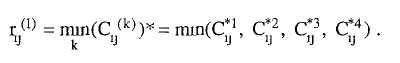
Эта операция гарантирует нам, что единицы будут стоять в результирующей матрице только для равноценных вариантов или тех вариантов, которые или превосходят вариант хj по каждому из критериев, или, по крайней мере, не уступают им.
Т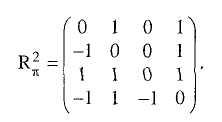 ак
из матрицы
ак
из матрицы
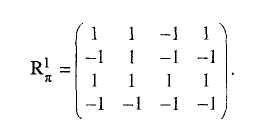
следует, что для пар (х1, х4), (х3, x1), (х3, х2), (х3, х4) первый элемент пары не уступает второму ни по одному из критериев.
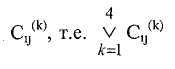
Дизъюнкция матриц обеспечивает, если в ней имеются
единицы, что хотя бы по одному из критериев вариант хi превосходит вариант хj. Тогда конъюнкция R я 1и R я 2означает, что вариант, имеющий 1 в результирующей матрице R я по одному из критериев, не уступает и хотя бы по одному превосходит другой элемент пары.
