Процедура выбора при наличии многих критериев

Пусть на множестве D задана некоторая совокупность критериев, т.е. функций D—>Re, Re - множество вещественных чисел. Оценку _i(х) вариан­та х по критерию _i, обозначим x⁽ⁱ⁾ и набор оценок одного и того же варианта в соответствии с разными критериями X = (х⁽¹⁾, ... x^(k)) — будем называть векторной оценкой варианта х. Векторные оценки вариантов y,z, ... будем соответственно обозначать Записьозначает, что х⁽¹⁾ у⁽¹⁾, ...,х^(к) у^(к) , а запись — что и . Будем говорить, что отношение R представлено набором критериев ₁ ..., _к, если xRy = . От­ношение R представлено набором критериев тогда и только тогда, когда оно является частичным порядком.

Правила выбора

Механизм выбора представляет собой пару М = , где — некотораясовокупность различных правил формирования отношений предпочтения на множестве вариантов D, а — правило выбора, указывающее, каким обра­зом выделить множество См(х) = С (х) с использованием заданного от­ношения. Рассмотрим наиболее часто используемые правила выбора .

1. Одно из наиболее распространенных правил предписывает выбор из предъявления X всех вариантов, для которых в X нет лучших, чем они:

Здесь R считается антирефлексивным, ибо в применении к рефлексивным отношениям этот способ дает пустой выбор.

2. При другом правиле из представления X выбираются лишь лучшие ва­рианты

Здесь R считается рефлексивным, поскольку для антирефлексивных от­ношений это правило дает пустой выбор.

3. Многокритериальный выбор по Парето. В этом случае отсутствует ка­кая-либо информация о важности критериев

4. Лексикографический выбор соответствует модели с упорядоченными критериями, в которой каждый предыдущий критерий существенно важнее предыдущих. Он осуществляется по правилу:

C_λ(x) = {xX(yX)( i 1, ….,k) (x⁽¹⁾=y⁽¹⁾ … x⁽ⁱ⁾ = y⁽ⁱ⁾  x⁽ⁱ⁺¹⁾y⁽ⁱ⁺¹⁾)}

При i = к член х^(i+|) < у^(i+|) игнорируется, и запись означает, что (х⁽¹⁾=у⁽¹⁾)

...(х^(к) = _У^(к)).

5. Мажоритарный выбор соответствует модели с равноценными крите­риями. Вариант х «предпочитается» варианту у, если х превосходит у по большему числу критериев, чем у превосходит х:

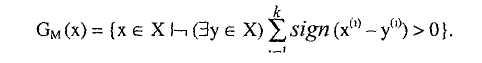
6. Совокупно-экстремальный выбор. Выбирается вариант, лучший хотя бы по одному из критериев:

7. Выбор по взвешенному критерию учитывает веса оценок: критерием _I i=l, ...,d приписывают веса 0, характеризующие их важность.

Функция выбора:

образуется вариантами с максимальной взвешенной суммой

Рассмотрим описание отношений, возникающих при использовании указанных выше критериев с использованием аппарата булевых функций.

Выбор по парето

С_л(х) можно рассматривать как выбор по отношению R_л, образованному по первому правилу:

Обозначим W_i — отношение частичного порядка, отвечающего критерию ,. Фиксируем некоторую пару (х, у) DxD и введем булевы переменные U_i, V_i, (i = 1,...,к):U_i=1(х,у)W_i,

Преобразуем (1) с учетом введенных обозначений:

Отсюда

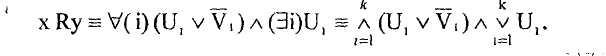
Поскольку х и у произвольны, это соотношение может быть записано в виде: