4.2. Модель информационной системы поддержки принятия решений

Информационное обеспечение решений осуществляется при помощи ин­формационных систем, устройство которых и требования к ним мы рассмот­рим с позиции общей теории систем. Как было показано в предыдущем раз­деле, принятие решения означает выделение некоторого подмножества в пространстве решений, другими словами, отношения. В свою очередь, дан­ное отношение может быть аппроксимировано композицией бинарных от­ношений. В конечном итоге оптимальный выбор определяет бинарное от­ношение посредством зависимостей, связывающих существенные параметры объекта. В связи с этим рассмотрим вопрос о том, как в информационной системе отображаются объекты и ситуации предметной области.

Общая теория систем изучает формальные взаимосвязи между наблю­даемыми признаками и свойствами. Пусть задано индексированное семейст­во множеств.

где I — множество индексов. Системой, заданной на V⁰, назовем некоторое собственное подмножество декартова произведения:

Компоненты V_i, i I называют объектами системы S. Частным случаем системы является система с двумя объектами — входным объектом X и выходным объектом Y

Если множество I конечно, то (1) можно записать в виде:

Пусть I_Х I и I_У I образуют разбиение множества I, т.е. пусть I_y I_x = Ø и I_y I_х = I. Множество X = {V_i: i I_Х} мы будем называть входным объектом, а множество Y = {V_i: i I_y} — выходным объектом системы. Тогда система S определяется отношением S X Y и называется системой «вход-выход». Если S является функцией, то соответствующая система бу­дет называться функциональной. Для данной системы S пусть С — произ­вольное множество, а функция R: (С х X) Y такова, что (х, у) S <=> (с)[R(c,x)=y], тогда С называется множеством или объектом состояний систе­мы, а его элементы — состояниями, функция R — реакция системы.

На интуитивном уровне информационная система представляет собою описание моделируемой предметной области в виде совокупности предло­жений об отдельных различных объектах и этих элементах. В свою очередь, объект предметной области может быть задан как множество истинных на нем предложений. Пусть D — фиксированное множество, элементы которого называются данными или утверждениями. Элементы D можно называть информационными объектами или конечными объектами данных. Одни элементы множества D могут быть менее информативными, чем другие. — обозначает специальный элемент из D как информационный объект с наименьшей информацией. Объект сам по себе не очень важен, однако иногда бывает полезно иметь объект, ведущий себя одинаково во всех сис­темах. Пусть Con(D) или просто Con обозначает выделенное множество ко­нечных подмножеств D. Элементы из Con трактуются как непротиворечивые множества информационных объектов или совместные множества утвер­ждений.

Информационной системой называется бинарное отношение

удовлетворяющее следующим свойствам:

Это свойство означает, что всякое данное совместно. Con содержит все одноэлементные множества.

Это свойство означает, что совместно любое множество совместного множества данных, т.е. Con как множество множеств, замкнутую относительно подмножеств.

для любого de D. Совместность множества данных сохранится, если добавить к нему любое его след­ствие.

Наименьшее по информативности данное следует из любого совместного множества.

Отношение |- обладает свойством рефлексивности.

где d₁ — любой элемент U, то V├ d.

(отношение ├ обладает свойством транзитивности).

Информационные объекты предназначены для описания определенных элементов предметной области (состояний системы), поэтому, используя информационный объект, мы описываем элемент предметной области, который является наименее определенным и обозначается через. Однаконе любая комбинация информационных объектов описывает возможный элемент предметной области, вследствие чего возникает необходимость понятия непротиворечивости. Если неверно, что U Con, то предложения из U не могут все одновременно выполняться на одном и том же объекте. В ин­формационной системе содержатся утверждения об отдельных различимых элементах или объектах предметной области. Различимость элементов сис­темой означает, что совокупность утверждений, известных ИС о конкретном объекте полностью его определяет.

Аксиома IS2 означает, что совместно любое подмножество совместного множества данных. В силу IS3 совместность множества данных сохранится, если добавить к нему любое его следствие. В силу IS4, наименьшее по ин­формативности данное следует из любого совместного множества. Аксиомы IS5 и IS6 являются аналогами рефлексивности и транзитивности.

Д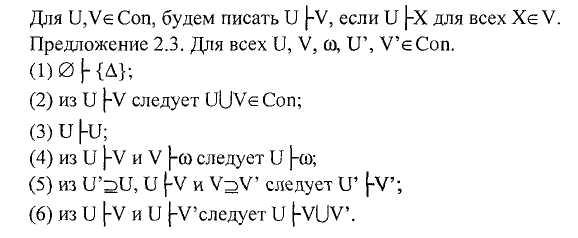ля записи зависимостей, существующих между предложениями, необ­ходимо ввести отношение следования. Смысл отношения U |-Х можно сфор­мулировать так: если все предложения из U истинны на некотором элементе, то X истинно на этом элементе.

Состояния системы

Пусть А — информационная система и пусть мы уже знаем, что зна­чит быть элементом данных или информационным объектом А. Предпо­ложим, что элементы данных XD_A представляют собой предложения о состоянии экономического объекта, поэтому, если X принадлежит D_A, a x — состояние экономической системы, то мы должны знать, что означает истинность X на х. Так как все, чем мы располагаем — это множество элементов данных D_A, мы должны предположить, что в нем содержится достаточно объектов, чтобы различать разные состояния. Формально можно сказать, что для двух состояний х и у х = у тогда и только тогда, когда все предложения XD_A, истинные на х, истинны на у, и обратно. Если принять этот принцип, то состояния можно отождествить с множе­ством истинных на них предложений; формально можно утверждать, что х={Х D_A │X истинно на х}.

Итак, для простоты в качестве множества состояний можно взять просто множество элементов данных или информационных объектов.

Неформально можно сказать, что множество всех истинных на некото­ром возможном состоянии предложений должно быть (1) непротиворечиво и (2) замкнуто относительно следования (т.е. дедуктивно замкнуто).

Определение 4.1. Состояниями экономического объекта (D_A, _A, Соn_А, |-_А) называются такие подмножества X множества D_A, что (1) все конечные подмножества X принадлежат Соn_А; (2) если Ux и U |- _АХ, то Хх. Утвер­ждение, что х является состоянием этой системы, записывается в виде х| │А│. Это множество состояний называется областью, которая определяет­ся данной системой. Состояние, не содержащееся ни в каком строго боль­шем состоянии (элементе) области, называется тотальным элементом; множество всех тотальных элементов обозначается через Tot_A.

Любое подмножество D_A, удовлетворяющее условию 3.1.(1) можно на­звать непротиворечивым. Замыкание любого непротиворечивого множества относительно следования дает элемент. Каждый элемент содержит _А как наименее информативное предложение на всех элементах. В каждой области существует наименьший элемент, содержащийся во всех остальных элемен­тах. Назовем его и дадим следующее формальное определение:

В этом определении вместо {_А} можно использовать пустое множество Ø, поэтому мы будем писать ├_АX.

Наименьший элемент области является нулем для . Операция моно­тонна относительно и между ними существует следующая связь:xy то­гда и только тогда, когда xy=x.

Нижняя грань. Для любого непустого подсемейства области |А| теоре­тико-множественное пересечение всех его элементов также является эле­ментом области. Это свойство превращает |А| в полную нижнюю полуре­шетку.

Что касается объединения, даже если х у является непротиворечивым, что не обязательно так, оно может оказаться не обязательно дедуктивно замкнуто относительно следования. Поэтому получить точные верхние гра­ни внутри |А| не так просто.

Обозначим точную верхнюю грань (если она существует в |А|) через х y. Элемент х у должен быть наименьшим элементом в |А|, который содер­жит (в смысле) оба множества х и у. ху существует тогда и только то­гда, когда в |А| имеется по крайней мере один такой элемент z, что xz и yz. Это равносильно непротиворечивости х у в |А|. Другими словами, точная верхняя грань семейства элементов существует тогда и только тогда, когда объединение элементов этого семейства непротиворечиво. В этом слу­чае точная верхняя грань представляет собой дедуктивное замыкание объединения. Если существует максимальный элемент ┬_А, то существуют все точные верхние грани и |А| является полной решеткой.

Областям соответствуют алгебраические решетки.

Предположим, что существует такая последовательность элементов х₀

Пусть у= х_n, тогда у очевидно подмножество D_A. Конечное подмножество у должно быть подмножеством одного из х_n, т.к. последовательность х_n является возрастающей. Но поскольку все члены этой последовательности являются элементами, они непротиворечивы. Следовательно, любое конеч­ное подмножество у непротиворечиво, поскольку, кроме того, х_n — множе­ство, замкнутое относительно ├_А, таковыми является и у. Другими словами, у является элементом. Область |А| замкнута относительно объединений воз­растающих целей элементов.

Пусть А — информационная система. Поскольку мы определяем элементы области |А| как множества, им можно придавать структуры, известные из обычной теории множеств. Например, теоретико-множественное отношение включения между множествами можно непосредственно применить к эле­ментам. При этом под включением ху мы понимаем, что любое истинноена х предложение (из имеющихся в информационной системе) истинно так­же на у. Мы будем говорить ху «х аппроксимирует у».

Очевидно, отношение рефлексивно и транзитивно. Будем говорить, что область |А| частично упорядочена по включению. Кроме отношения упорядочения введено еще отношение доминирования. Произведение отношений доминирования эквивалентно включению.

Предположим, что х и у — два элемента. Элементы — это непротиворе­чивые дедуктивно замкнутые множества объектов данных. Пересечение х

у также непротиворечиво и дедуктивно замкнуто. Это означает, что область |А| является нижней полурешеткой.

Элемент _А часто называют дном области. Верха или максимального элемента ┬_A может и не быть. Существование такого элемента возможно тогда и только тогда, когда все конечные подмножества D_A непротиворечи­вы, в этом случае множество ┬_A равно D_A. Такая возможность не исключена, однако в ней нет необходимости. Если элемент ┬_A существует, то он единст­венный тотальный элемент области и обратно.

Рассмотрим информационную систему А. Для uCon_A определим соответствующую окрестность в |A|[u]_A={x |А| | u х}. Изучение и построение окрестностей существенно для выбора оптимальных решений как преобра­зований истинных формул, описывающих состояние экономического объек­та. Поиск преобразования — вывода переводящего истинные в одном со­стоянии формулы в формулы, истинные в другом, желаемом состоянии — составляет суть поиска решения. Существенно, что состояния принадлежат к различным классам и не для всякой пары классов имеется преобразование, переводящее состояния одного класса в состояния другого.

Динамическая проблема решения в общих чертах может быть описана в терминах поиска агентом оптимального плана. План состоит из цели (под­множество состояний с наивысшими значениями полезности) и последова­тельности решений P={S U (SxT) }, принятых для достижения цели и исхо­дов, связанных с этими решениями. Здесь S — множество состояний, (SxT) — транзитивное замыкание множества пар (s, t), где t — момент време­ни t Т.

Существует вероятность и полезности, связанная с каждым исходом, и агент выбирает акты решений, которые максимизируют ожидаемую полезность. Проблема решения нахождения оптимального плана может быть опи­сана как динамическая задача максимизации, имеющая следующую структу­ру решения:

Max EU(D(t), S(t)) при условии S(t+1) = R(D(t), S(t), где переменные и основные черты проблемы решения состоят в следующем.

D(t): пространство решений в момент t или конечное пространство потенциальных актов. Агент может выбрать специфический акт {d(t)_i} из мно­жества к возможных актов решений D(t)={ d(t)₁, d(t)₂,..., d(t)_k}.

S(t) — пространство состояний в момент t. Конечное пространство исходов мира: S(t)={s(t)₁ s(t)₂,..., s(t)_i}.

Функция полезности в пространстве состояний S(t) каждому решению d(t)_i приписывает полезность U(d(t)_i, s(t)) каждого возможного исхода (пере­хода) в момент t

P(s(t)/d(t)_i): вероятность перехода в состояние s(t) при условии решения d(t). Для каждого решения d(t) ЛПТ прямо или косвенно приписывает меру совместного распределения вероятностей.

R(D(t), S(t)): правила перехода. Множество правил, которые переводят пару состояние, решение в новое состояние (S(t)x D(t)) —•> S(t+1).

EU(t): ожидаемая полезность в момент t. Для каждого решения и всех ис­ходов в момент t связанная с ними полезность умножается на соответст­вующие условные вероятности. EU(t) =

Агент, используя базу знаний, генерирует множество возможных струк­тур решения и затем испытывает эти структуры, чтобы найти ту, которая обеспечивает наилучшие результаты при ограниченных ресурсах.

Агент использует обучение, под которым мы понимаем любое изменение базы знаний, которое позволяет агенту достичь большей общей полезности в тот же интервал времени.

Программа обучения должна обладать некоторыми возможностями к обобщению, что позволяет увеличить полезность при рассмотрении анало­гичных проблем решения. В процессе обучения агент действует одним из следующих способов.

1. Обучается событиям или узлам сети. В базе знаний хранится большое количество фактов, но только некоторые из них релевантны рассматриваемой ситуации. Обучение заключается в выделении подмножества фактов (утверждений), релевантных ситуации.

2. Обучается дугам байесовской причинной сети, т.е. производит выделение подграфа, релевантного проблеме.

3. Обучается параметрам. Это обучение заключается в том, что агент не может и не знает, какие количественные характеристики следует ввести о проблеме, в том числе и данные о предпочтениях (полезности).

Агент рассматривает укрупненное или качественное описание проблемы, находит прототип в базе знаний и делает в новой структуре оценки недостающих или пропущенных параметров, опираясь на аналогию с другими примерами.

Определим объединение множества актов решения и множество исходов как множество событий. Состояние, в котором находится в данный момент система, назовем действительным миром агента. Совокупность возможных состояний, в которые система переходит в результате событий, называется возможными мирами.

Пусть Р = {p₁, p₂,..., р_n} — множество предложений, описывающих собы­тия в момент t. Определим предложение как истинное по отношению к возможному миру, если он интерпретируется как истинное, используя интерпретацию, связанную с возможным миром.

Определим множество возможных миров в момент t как 2^Р. Каждое подмножество Р описывает возможный мир W(t)_i в момент времени t и каждая возможная комбинация событий представлена в некотором возможном мире.

Представим множество возможных миров в момент t двоичной матрицей W=[W(t)_ij], где j-й столбец соответствует j-му событию и i-я срока представ­ляет i-ый возможный мир. События, которые являются истинными в i-м воз­можном мире, представлены единицами в соответствующем столбце в стро­ке i.

Проблема генерирования множества возможных миров и идентификация ближайшего к действительному миру агента является проблемой экспонен­циальной сложности. В случае m событий число возможных миров в момент t равно 2^m. Но это еще не включает переходы от возможных миров в W(t) в возможным мирам в W(t+1). В этом и заключается проблема обучения правилам перехода.

Пусть d(t)_i — акт решения, который агент может выполнить. Предположим, что принятие решения и имплементация выполняются одновременно. Определим мир решения как возможный мир, который существует до теку­щего момента и который до некоторой степени походит на тот мир, в кото­ром агент принял решение выполнить d(t)_i в момент t. Пусть dW(t)^*_i — мир решения, который в момент t является ближайшим миром к реальному миру. Агент принял решение, которое максимизирует его оценку полезности, ос­нованную на его предсказании возможных миров, которые являются дости­жимыми из множества миров решения.

Вследствие недостатка информации о реальном мире и ограниченных вычислительных ресурсах будет существовать не один возможный мир, а много.

Пусть агент генерирует матрицу возможных миров в момент t+1. Определим отношение перехода r(dW(t)_i^*, W(t+1)) между ближайшим миром ре­шения в момент t и i-м подмножеством возможных миров W(t+1)_i, в которое dW(t)_i* могут быть переведены. Обозначим возможный мир, ближайший к действительному миру, проистекающему из dW(t_i)^* (это тот мир, который агент принимает за реальный), как W(t+1)_i^*.

Если бы вселенная была детерминированной, и агент овладел совершенной информацией и был всезнающим, тогда он бы знал отношение r(dW(t_i)^* ,W(t+l)_i*). Ограниченные ресурсы и несовершенная информация заставляет агента довольствоваться обобщением W(t+l)_i*, представленным некоторым подмножеством возможных миров из W(t+1)_i*.

Для того чтобы бороться с экспоненциальным ростом сложности задачи, мы должны постараться ограничиться только малым подмножеством возможных миров и отношений перехода.

Один из возможных подходов заключается в анализе причинных зависимостей. С этой целью могут быть использованы абдуктивные выводы, по­пытки объяснить, почему наступило то или иное решение.

Абдуктивные выводы по отношению к проблеме решения можно описать как поиск наиболее вероятного мира решений dW(t-l)_i* из множества возможных миров W(t-l) при условии наличия данных W(t)_i^* . Когда дана про­блемная ситуация в момент t, агент должен понять причины и условия в мо­мент t-1 для того, чтобы принять решение, максимизирующее полезность в момент t+1.

Множество действий, доступных агенту в данной ситуации, может быть представлено переменной или группой переменных. Выбирая действия, агент оценивает последствия своего выбора. Для каждого состояния s множества S, s S мы принимаем меру полезности U(s), представляющую сте­пени желательности, тогда общая ожидаемая полезность, связанная с дейст­вием d, определяется U(d) = U(s)P(s/d,x), где P(s/d,x) — распределение вероятностей последствий состояния s при условии выбора действия d и на­блюдаемых данных х. Решение агентом принимается на основе максимума ожидаемой полезности

Последствия действий являются состояниями, и они описываются совокупностью истинных в них утверждений.