3А) Находим матрицу , обратную к , методом присоединённой матрицы, по формуле: , где:

,

,

,

.

Тогда .

1б) Находим вектор 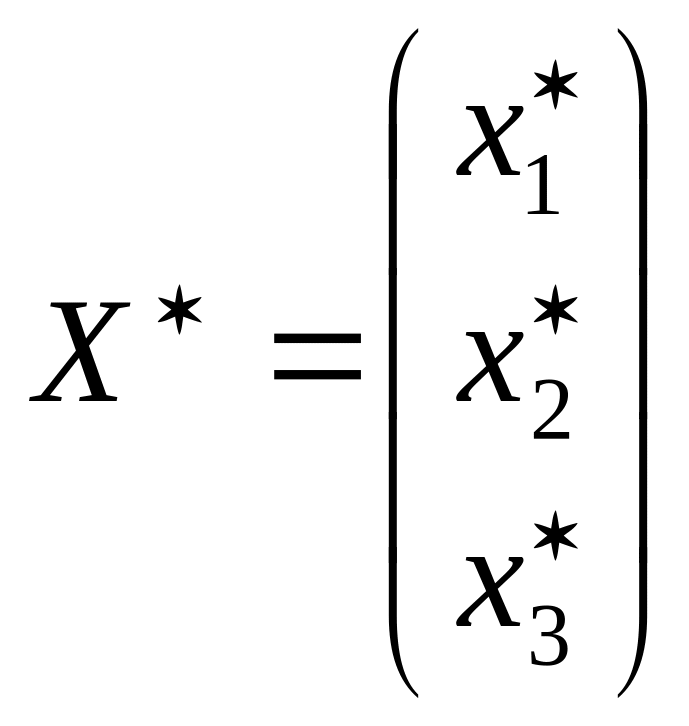валового выпуска на вектор конечного продукта в плановом периоде, следующим за отчётным (в предположении, что матрица , называемая также технологической, а, следовательно, и матрица не изменяются, т.е. ) по формуле:

.

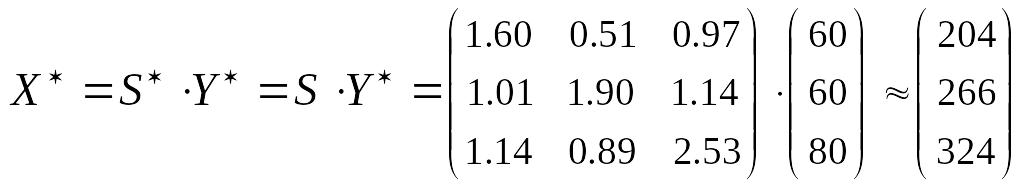2б) Находим по формуле ( ) плановые межотраслевые поставки , округляя полученные значения до целых (с учётом балансовых соотношений , ):

, , ,

, , , , , .

3б) Плановые объёмы выпуска чистой продукции каждой из отраслей находим по формуле :

, ,

.

Ответ: Межотраслевой баланс планового периода имеет вид:

Отрасли производства	Отрасти потребления			Конечный продукт	Валовой продукт
	I	II	III
I	20	27	97	60	204
II	61	80	65	60	266
III	61	53	130	80	324
Чистый продукт	62	106	32
Валовой продукт	204	266	324

6.2. Краткие теоретические сведения.

Тема 1. Определители.

Квадратной матрицей порядка называется квадратная таблица из чисел ( , ): , состоящая из строк и столбцов. У квадратной матрицы различают главную диагональ: и побочную диагональ: . Любой квадратной матрице порядка можно поставить в соответствие число 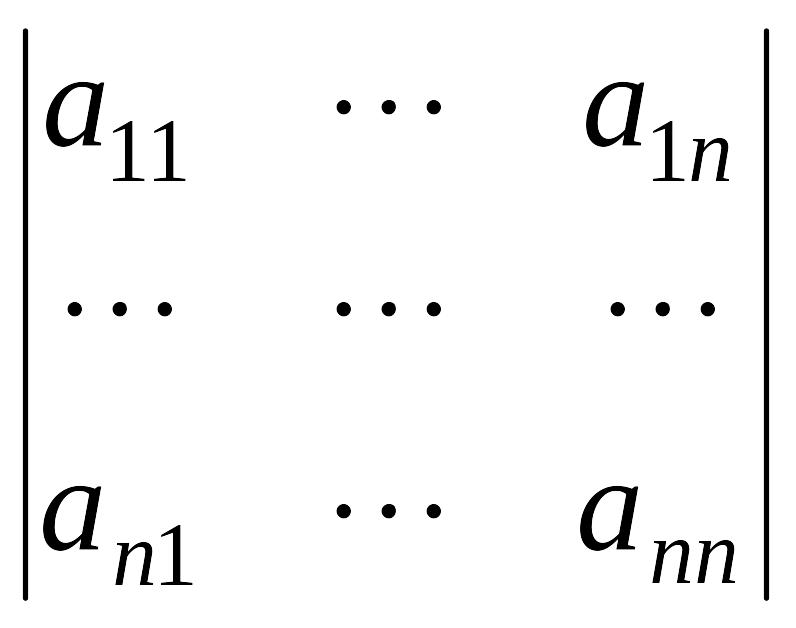, равное алгебраической сумме слагаемых, составленных определённым образом из элементов матрицы , называемое определителем матрицы. Кратко обозначается , .

Определителем 1-ого порядка называется число .

Определителем 2-ого порядка называется число

.

Определителем 3-его порядка называется число

.

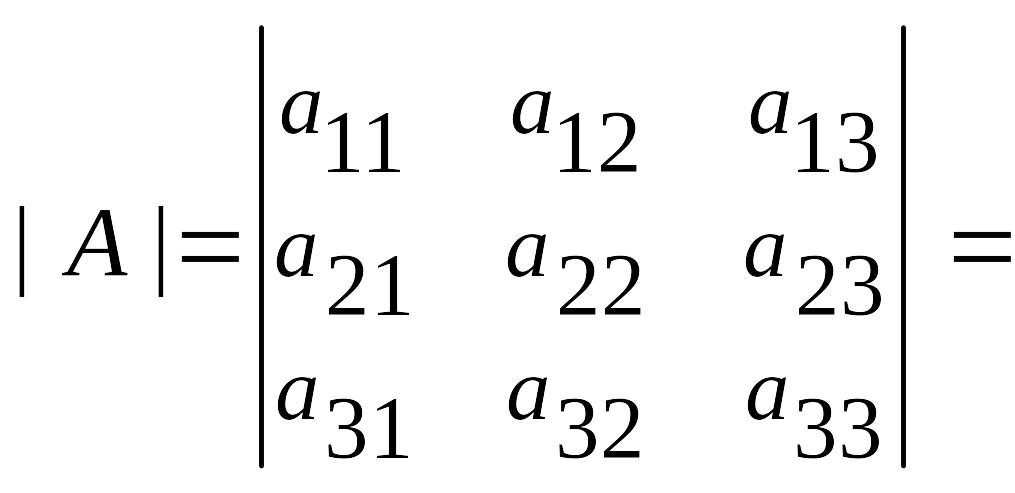
Минором элемента называется определитель , полученный из определителя вычёркиванием -ой строки и -ого столбца.

Алгебраическим дополнением элемента называется его минор , взятый со знаком :

.

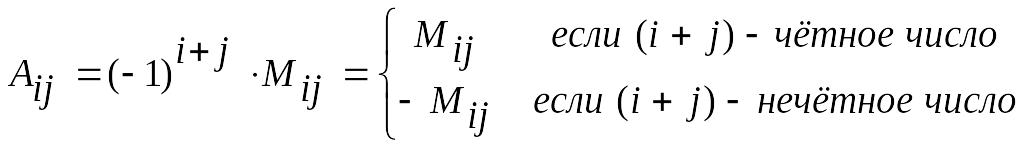Определителем порядка называется число

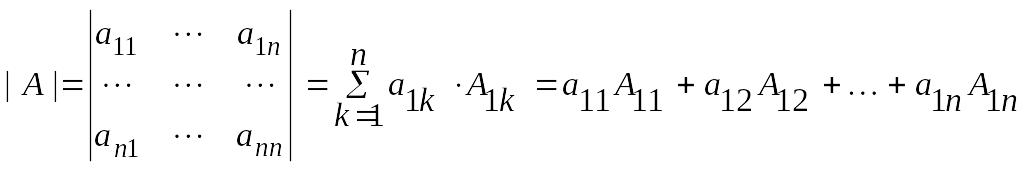
Разложением определителя по -ой строке ( ) называется соотношение: .

Разложением определителя по -ому столбцу ( ) называется соотношение:

Определители обладают следующими свойствами:

1) определитель не изменится при замене всех его строк столбцами с теми же номерами;

2) определитель изменит знак на противоположный, если переставить местами любые две строки (два столбца) определителя;

3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;

4) определитель равен нулю, если он содержит нулевую строку (столбец), две одинаковые или пропорциональные строки (столбца);

5) определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число;

6) определитель треугольного вида (когда все элементы, лежащие по одну сторону одной из его диагоналей равны нулю) равен произведению диагональных элементов: .