Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство.

Арифметическим вектором называют упорядоченную совокупность из чисел: и обозначают . Числа называют компонентами вектора , число компонент называют его размерностью.

Векторы и называют равными, если они одинаковой размерности и их соответствующие компоненты равны: , .

Суммой векторов и одной размерности, называют вектор той же размерности, для которого: , .

Произведением вектора на число называют вектор той же размерности, для которого: , .

Линейной комбинацией векторов и одной размерности, называют вектор той же размерности ( и - произвольные числа), для которого: , .

Множество всех -мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторным пространством и обозначают .

Систему векторов называют линейно зависимой, если найдутся числа , одновременно, такие, что (где - нулевой вектор), в противном случае, систему называют линейно независимой.

Базисом системы векторов называют упорядоченную систему векторов , удовлетворяющую условиям:

1) , ; 2) система линейно независима; 3) для любого вектора найдутся числа такие, что . Коэффициенты , однозначно определяемые вектором , называют координатами вектора в базисе , а формулу называют разложением вектора по базису и пишут: .

В пространстве базисом является каждая упорядоченная система из линейно независимых векторов: . Формулу называют разложением вектора по базису , коэффициенты - координатами вектора в базисе и пишут .

Всякая упорядоченная система из векторов образует базис , если определитель, столбцами которого являются компоненты векторов , не равен нулю.

Пространство , в котором введено скалярное произведение векторов, удовлетворяющее определённым требованиям (аксиомам), называют евклидовым. Скалярным произведением двух векторов и называют число: .

Тема 5. Линейные операторы. Собственные числа и векторы.

Оператором называется закон (правило), по которому каждому вектору ставится в соответствие единственный вектор , и пишут или В дальнейшем, рассматривается случай (преобразование пространства ). Оператор называется линейным, если для любых векторов и действительных чисел выполнено условие: .

Если - базис пространства , то матрицей линейного оператора в базисе называется квадратная матрица порядка , столбцами которой являются столбцы координат векторов . Между линейными операторами, действующими в и квадратными матрицами порядка , существует взаимно однозначное соответствие, что позволяет оператор представить в матричном виде , где - матрицы-столбцы координат векторов , - матрица оператора в базисе .

Для линейных операторов, действующих в вводятся следующие операции: 1) сложение операторов: ; 2) умножение операторов на число: ; 3) умножение операторов: .

Обратным к оператору называется оператор такой, что , где - единичный (тождественный) оператор, реализующий отображение . Обратный оператор существует только для невырожденных операторов (операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.

Пусть число и вектор , , таковы, что выполняются равенства: или . Тогда число называется собственным числом линейного оператора (или матрицы ), а вектор - собственным вектором этого оператора (или матрицы), соответствующим собственному числу . Равенство может быть записано в виде , где - единичная матрица порядка , - матрица-столбец координат собственного вектора , соответствующего собственному числу , - нулевая матрица-столбец.

Характеристическим уравнением оператора (или матрицы ) называется уравнение: .

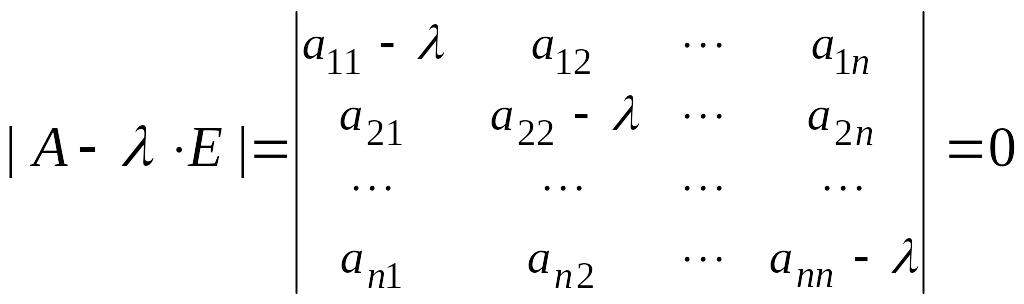Множество собственных чисел оператора (или матрицы) совпадает с множеством корней его характеристического уравнения: , а множество собственных векторов, отвечающих собственному числу , совпадает с множеством ненулевых решений матричного уравнения: .