1.6 Поля физических величин. Элементы тензорного анализа.

В гидродинамике в основном используется Эйлерова система отсчета, в ней оперируют не с постоянными векторами и тензорами, а с полями скалярных, векторных и тензорных величин. Компоненты векторов и тензоров являются функциями координат и времени. При описании движения жидкости возникает необходимость дифференцирования скалярных векторных и тензорных полей – полей плотности, давления, скоростей, напряжений и других физических величин.

– полей плотности, давления, скоростей, напряжений и других физических величин.

Полем физической величины (она может быть скалярной , векторной , тензорной ) называется совокупность значений этой величины для любой точки пространства и для любого момента времени. На рисунке 1.12 показано положение точки, определяемое радиус-вектором для произвольного момента времени .

Рисунок 1.12 – Радиус–вектор точки в декартовой прямоугольной системе координат.

Положение точки в пространстве определяется радиус-вектором , который можно записать в следующем виде, используя индексную форму записи:

или просто:

если учитывать соглашение осуммировании по повторяющемуся индексу.

Задать поле физической величины – это значит задать зависимость

(1.6.1)

Если зависимости от времени нет, то поле называется стационарным, если уже нет зависимости от координат, то поле называется однородным. Для стационарного поля:

(1.6.2)

для однородного нестационарного поля:

(1.6.3)

для однородного стационарного:

(1.6.4)

В качестве примеров физических полей приведем следующие, заданные для простоты, в виде некоторых степенных функций координат и времени:

– поле давлений, заданное скалярной функцией:

(1.6.5)

– поле скоростей, заданное вектор-функцией:

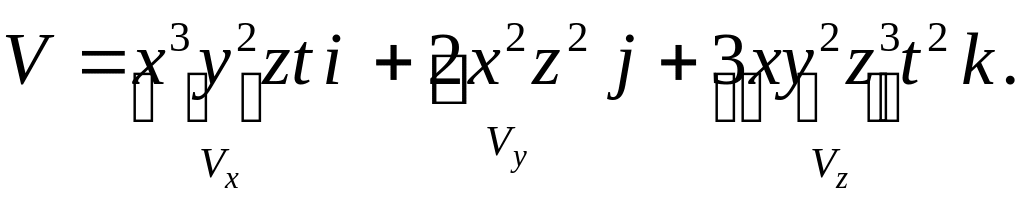(1.6.6)

– поле напряжений , заданное тензорной функцией с компонентами:

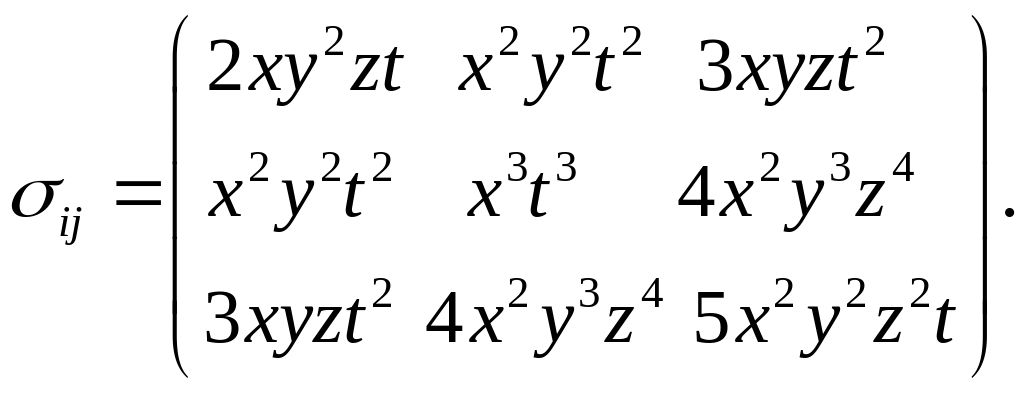(1.6.7)

Для каждой точки пространства и для любого момента времени этим полям соответствуют свои числовые значения. Так, для точки при имеем:

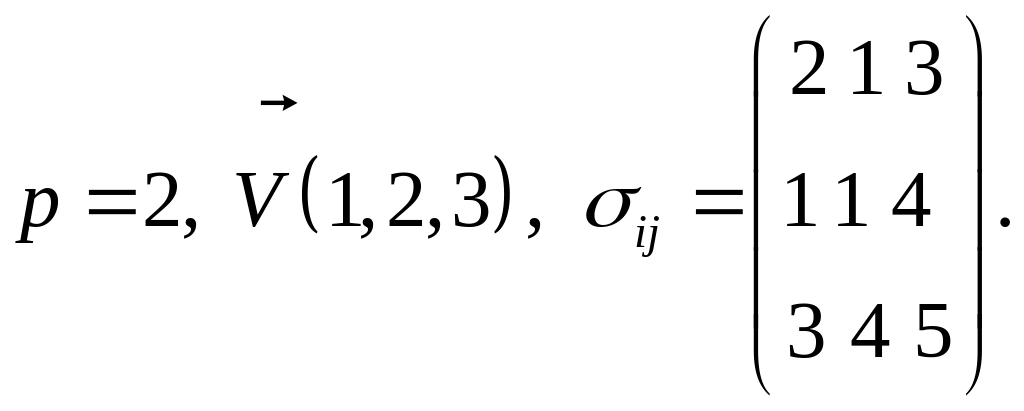
Неоднородность полей характеризуется линейными дифференциальными операторами-градиентом , дивергенцией , ротором , которые являются операторами первого порядка (содержат частные производные первого порядка), а также дифференциальным скалярным оператором второго порядка – лапласианом .

Эти операторы можно определить через векторный дифференциальный оператор – оператор Гамильтона (набла) . В декартовой прямоугольной системе координат он имеет вид:

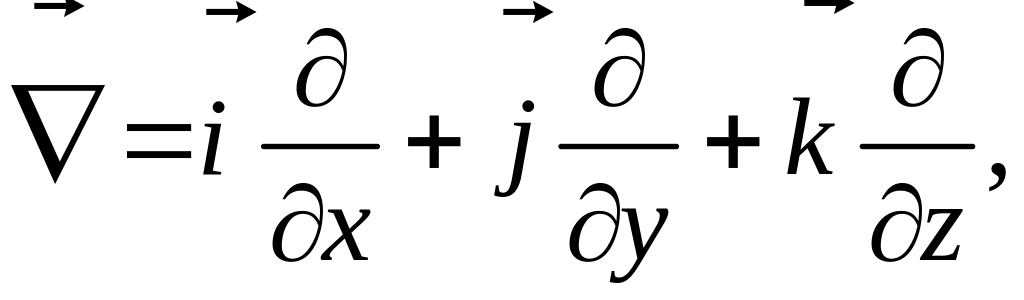(1.6.8)

или, используя индексную форму записи:

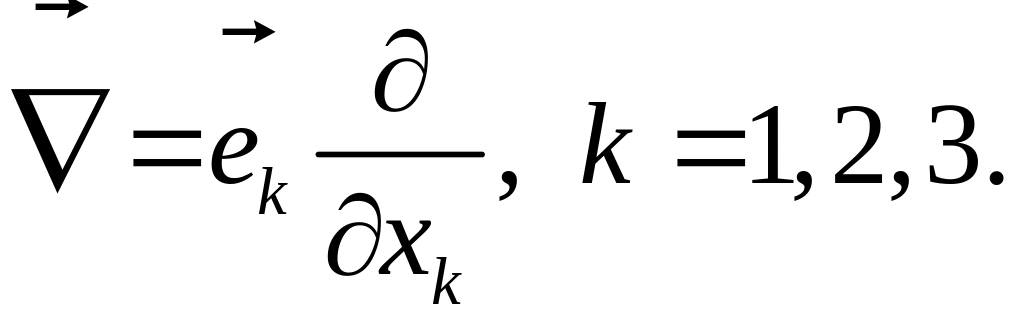(1.6.9)

Все дифференциальные операции над скалярными, векторными и тензорными величинами, выражаются инвариантным образом через оператор . Запишем эти операции и подробно выразив их через и применим в дальнейшем в качестве упражнения, к полям, заданным выражениями (1.6.5), (1.6.6) и (1.6.7).

Градиент скалярной функции является вектором, он характеризует направление наибольшего возрастания функции и быстроту этого возрастания. Через оператор Гамильтона (набла) он записывается так:

(1.6.10)

В компонентном виде:

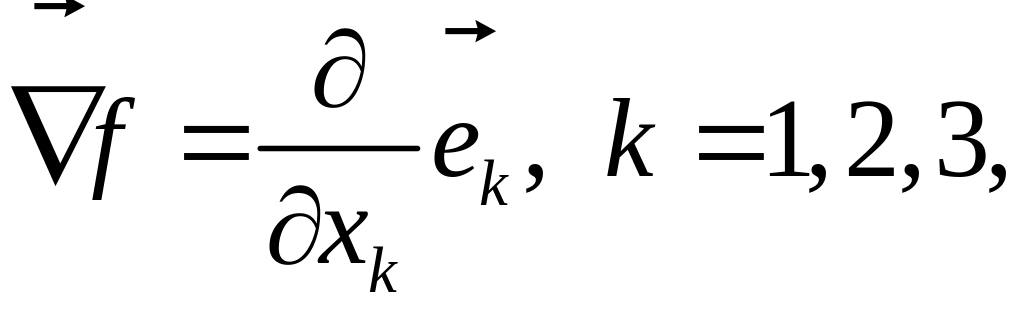(1.6.11)

или, в развернутом виде, переходя к обычным обозначениям для декартовой прямоугольной системы координат:

Таким образом, градиент скалярной функции есть вектор с компонентами , т.е.:

Упражнение 1. Вычислим для поля давлений, заданного выражением (1.6.5):

В точке при это вектор

Градиент вектор-функции является тензором второго ранга. Так, для вектора :

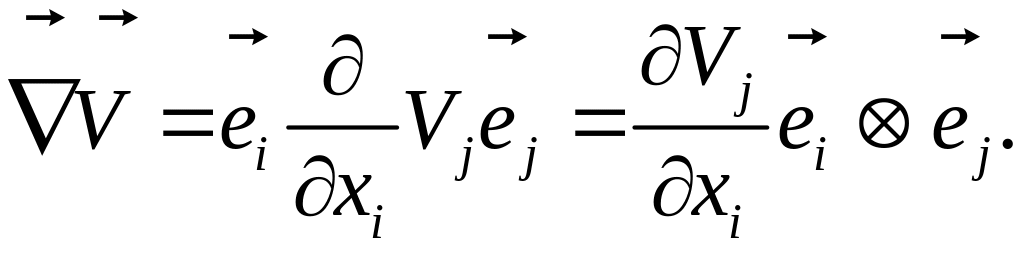(1.6.12)

Если – вектор скорости, то этот тензор градиентов скоростей в гидродинамике разбивают на симметричную и антисимметричную части:

(1.6.13)

где симметричная часть

(1.6.14)

называется тензором скоростей деформаций, а антисимметричная

(1.6.15)

– тензором вращения (спином).

В компонентном виде:

(1.6.16)

(1.6.17)

Матрицы их компонент:

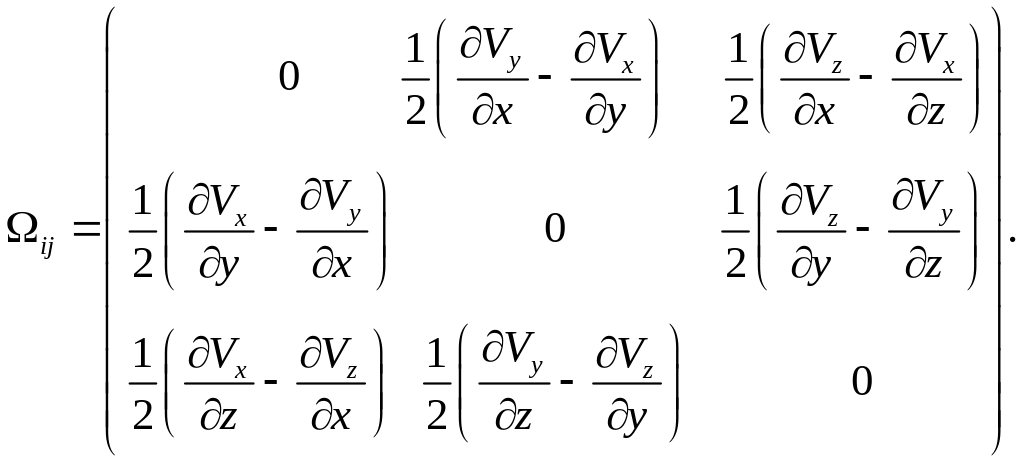
Упражнение 2. Для поля скоростей, заданного выражением (1.6.6) вычислим тензоры и :

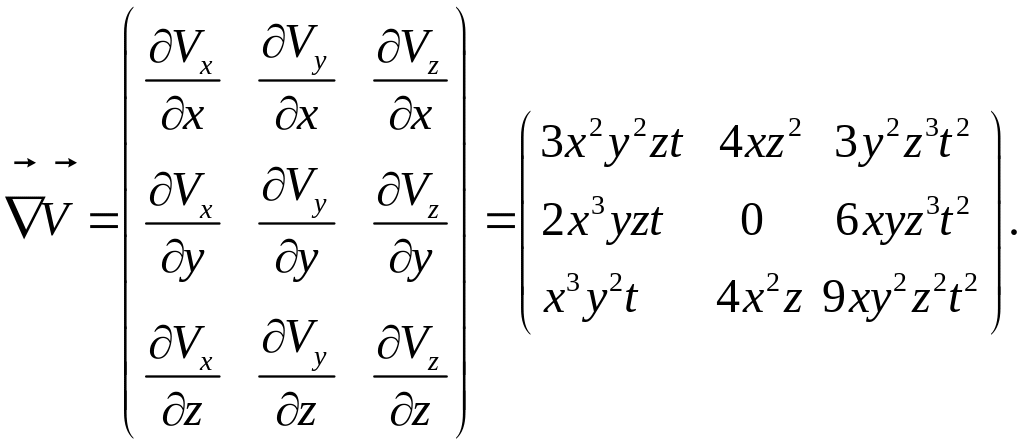
В точке в момент этот тензор второго ранга и его транспонированный имеют компоненты:

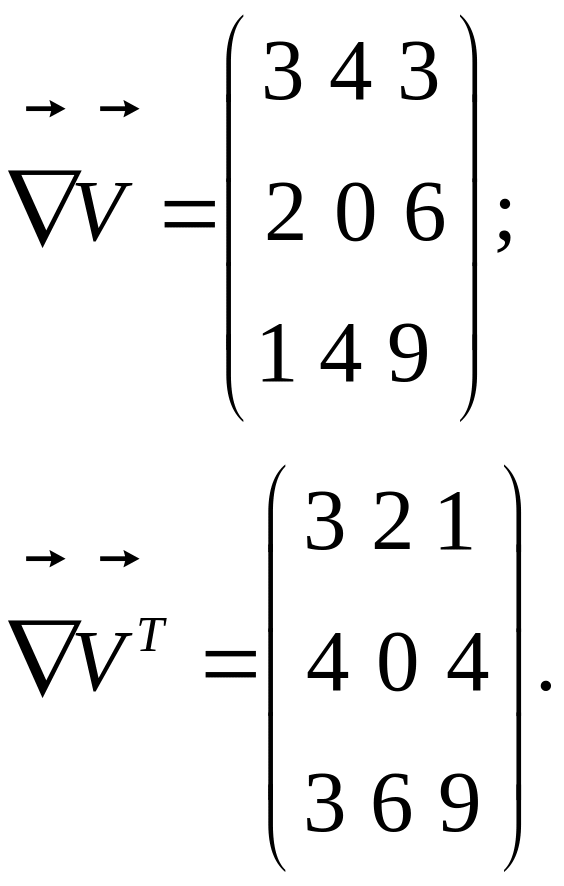
Следовательно компонентами тензоров скоростей деформаций и тензора вращения будут:

Видно что матрица компонент тензора симметрична относительно главной диагонали, матрица компонент – антисимметрична, на ее диагонали всегда находятся нули.

Дивергенция вектор-функции характеризует разность потоков вектора, входящего и выходящего в рассматриваемый объем пространства. Через оператор она записывается как результат скалярного произведения вектора и соответствующего вектора, например :

(1.6.18)

В терминах компонент эта скалярная величина записывается в виде:

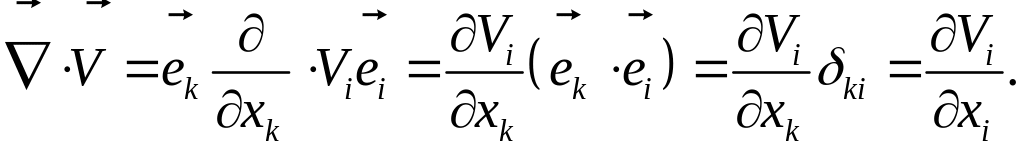(1.6.19)

Здесь учтено, что производные базисных векторов по координатам равны нулю 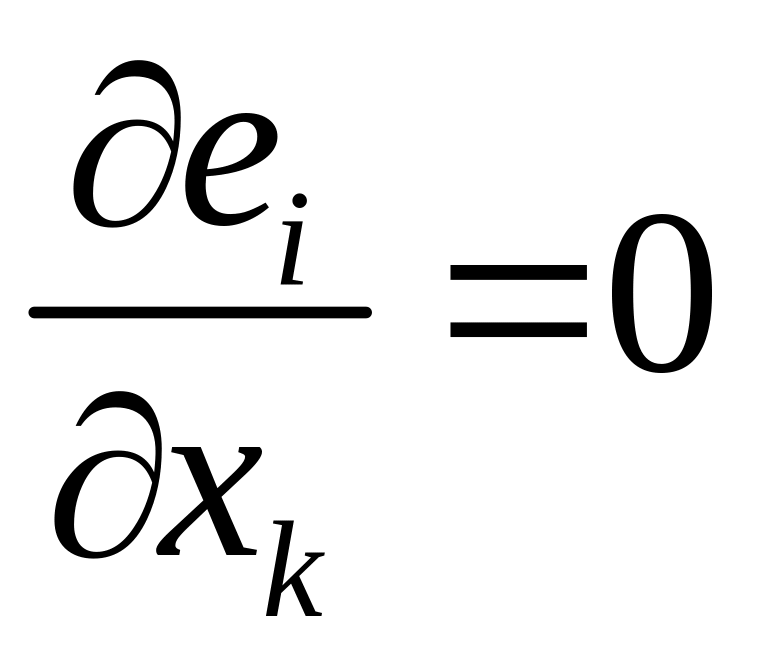, поскольку базисные векторы декартовой прямоугольной системы координат не меняются от точки к точке ни по величине, ни по направлению. В развернутом виде для декартовой прямоугольной системы координат имеем:

(1.6.20)

Упражнение 3. Вычислим дивергенцию поля скоростей, заданного выражением (1.6.6):

В точке при эта скалярная величина есть число .

Дивергенция тензора второго ранга дает векторную величину:

(1.6.21)

или в развернутом виде:

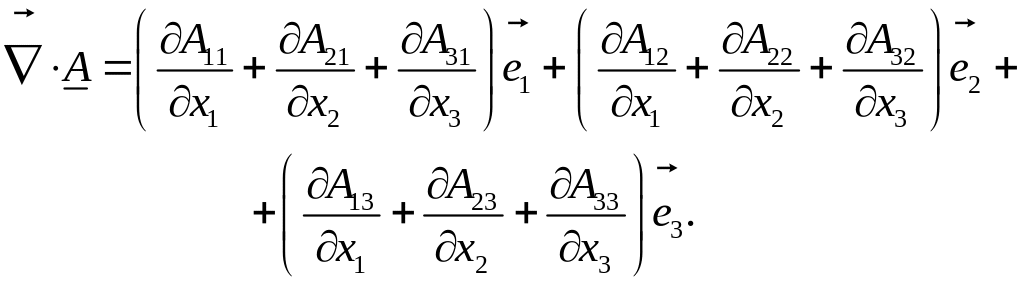(1.6.22)

Упражнение. Для тензора , заданного согласно выражения (1.6.7), найдем его дивергенцию:

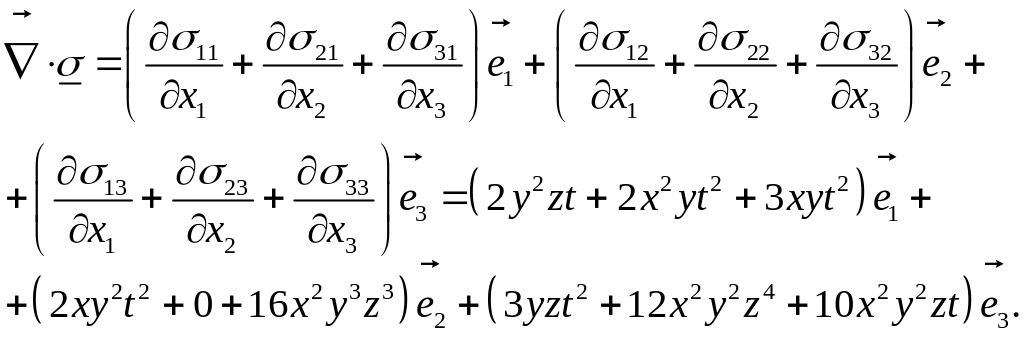
В точке при это будет вектор

Ротор вектор-функции есть вихрь, через оператор ротор вектора скорости записывается как результат векторного произведения:

(1.6.23)

Используя альтернируюий тензор Леви-Чивита эту величину можно записать в компонентном виде следующим образом:

(1.6.24)

Распишем компоненты этого вектора по осям декартовой прямоугольной системы координат:

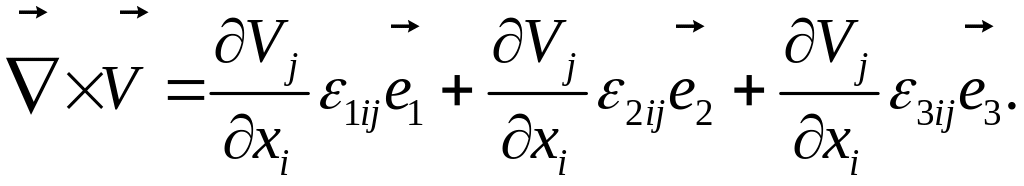
Для первого слагаемого – компоненты ротора относительно оси компонента тензора Леви-Чивита принимает значение, равное 1 при и значение -1 при , т.е. . Тем самым

Для второго слагаемого имеет ненулевые значенияли , и если – в первом случае , во втором . Тогда компонента при базисном векторе имеет значения

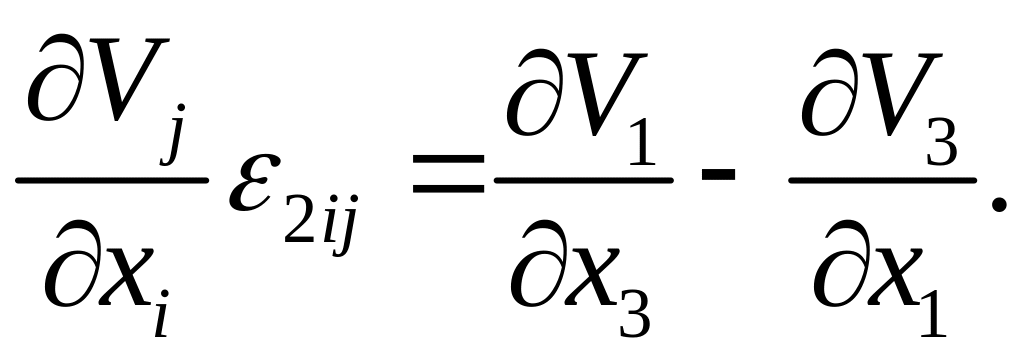
И, наконец, для третьего слагаемого имеем , когда и , если . В результате это слагаемое принимает вид:

В итоге имеем выражение для ротора вектора в компонентном виде, в обычной форме записи для декартовой прямоугольной системы координат:

(1.6.25)

Замечание. Менее громоздкие выкладки получаются, если этот вектор вычислять через определитель:

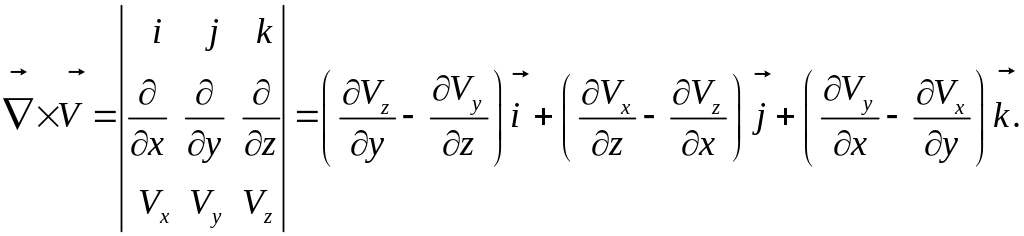
Упражнение 4. Вычислим вихрь скорости для , заданного выражением (1.6.6):

В точке при это вектор .

Ротор тензорной функции второго ранга будет тензорной величиной также второго ранга:

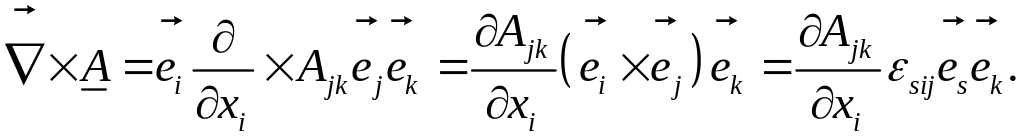(1.6.26)

Упражнение 5. Вычислим компоненту при базисной диаде ротора тензора напряжений , заданного выражением (1.6.7):

При базисной диаде , когда , находится компонента

Если взять базисную диаду (здесь индексы ) то ее компонента:

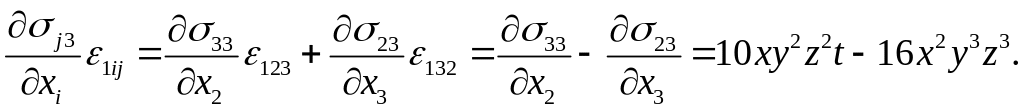
В точке при рассмотренные компоненты равны, соответственно 12 и -6.

Лапласиан есть скалярный дифференциальный оператор второго порядка, это результат скалярного произведения вектора Гамильтона (набла) самого на себя:

(1.6.27)

или, в компонентном виде:

(1.6.28)

Примечание. Записывать этот оператор в виде недопустимо, т.к. в этом случае пропадает правило суммирования по повторяющемуся индексу.

Более подробно, для декартовой прямоугольной системы координат оператор Лапласа записывается в виде:

(1.6.29)

Этот скалярный оператор второго порядка можно применять к любым тензорным величинам – он не изменяет ранг тензора.

Для скалярной функции ее лапласиан записывается следующим образом:

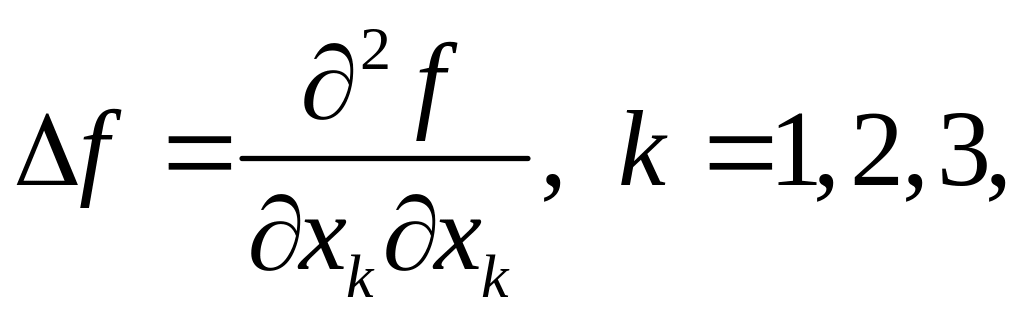(1.6.30)

или, более подробно:

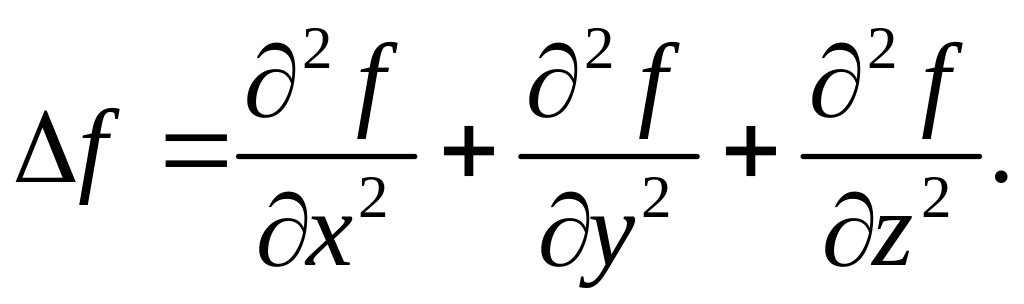(1.6.31)

Упражнение 6. Вычислим лапласиан поля давлений, данного выражением (1.6.5)

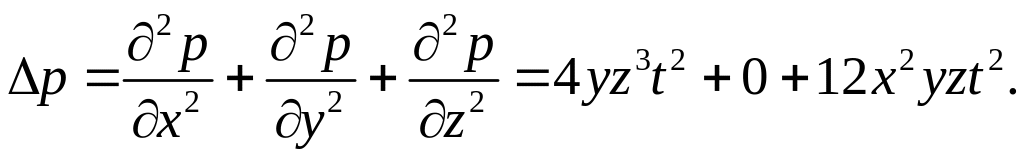
В точке при это число .

Лапласиан вектора является векторной величиной:

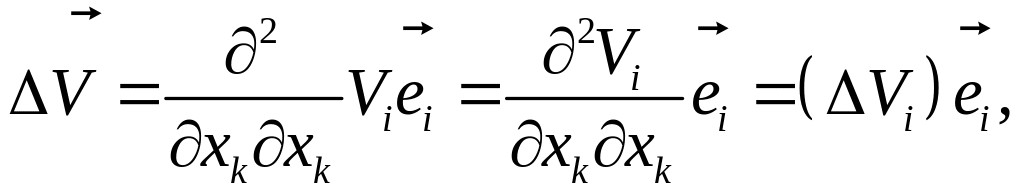(1.6.32)

здесь к каждой компоненте вектор–функции применяется оператор Лапласа.