1.4. Элементы тензорной алгебры. Простейшие операции над тензорами.
1) Умножение на
число – каждая компонента умножается
на одно и то же число. Например,
в компонентном виде записывается
следующим образом:
(1.4.1)
2) Сложение тензоров
одинакового ранга:
.
В терминах компонент это:
(1.4.2)
3) Скалярное
произведение тензоров – скалярно
перемножаются два соседних базисных
вектора, результат – новый тензор –
имеет ранг на два меньший суммы рангов
исходных тензоров. Пусть, для примера
Их скалярное произведение дает тензор третьего ранга:
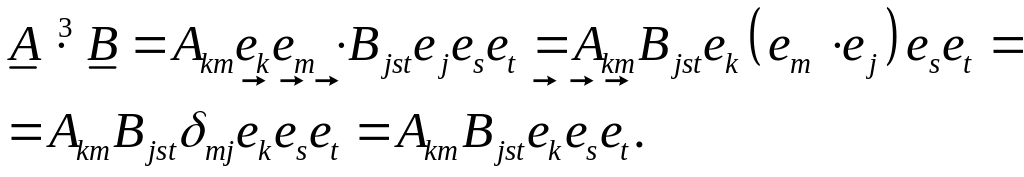(1.4.3)
Примеры:
а) скалярное произведение векторов и тензоров:
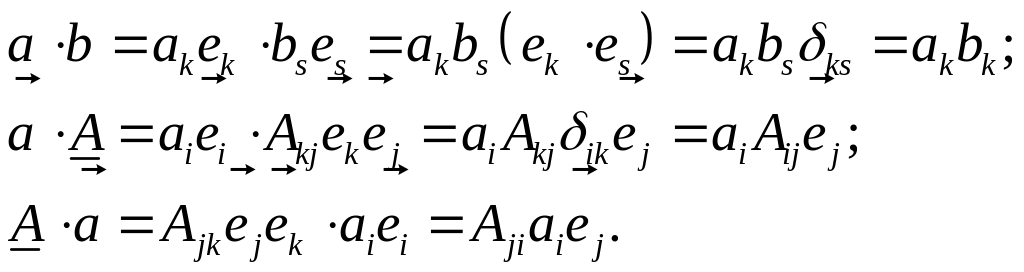
Таким образом
.
б) умножение на единичный тензор (справа и слева):
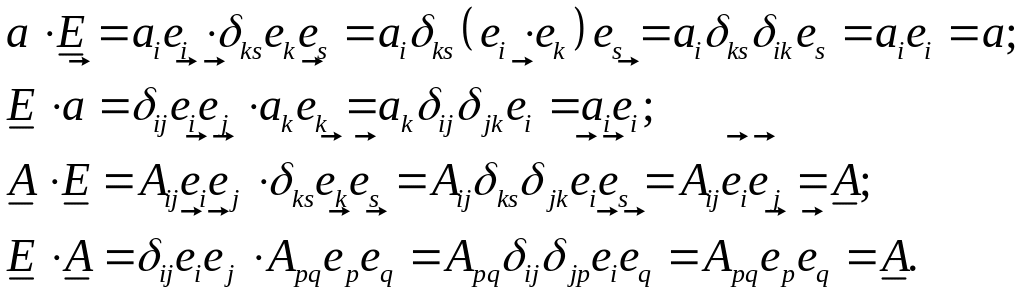
Таким образом, умножение на единичный тензор не меняет исходного тензора.
4) Степени тензоров.
В компонентном виде:
(1.4.4)
5)Двойное скалярное
произведение тензоров (двойная свертка)
– перемножаются две пары соседних
базисных вектров. Пусть
для них двойное скалярное произведение
есть
(1.4.5)
Ранг полученного тензора на четыре меньше суммы рангов исходных.
6) Тензорное произведение тензоров.
Для тензоров
и
,
например, которые в компонентном виде
записываются следующим образом:
тензорное произведение есть новый
тензор, ранг которого равен сумме рангов
тензоров:
(1.4.6)
Заметим, что
скалярное произведение этих тензоров
и
представляет собой свертку по двум
индексам ( в данном случае по
и
):
а их двойное скалярное произведение –
двойную свертку ( по индексам
и
в данном случае):
Упражнение: показать, что для тензорной единицы и произвольного вектора справедливы равенства:
а)
б)
в)
7) Транспонирование тензоров.
Пусть дан некоторый
тензор второго ранга
.
Тензор
называется транспонированным (сопряженным)
по отношению к тензору
,
если для любого вектора
выполняется равенство:
(1.4.7)
Отсюда следует,
что для тензора
сопряженным является тензор
,
что означает, что в матрице компонент
произошла замена строк на столбцы.
Действительно:
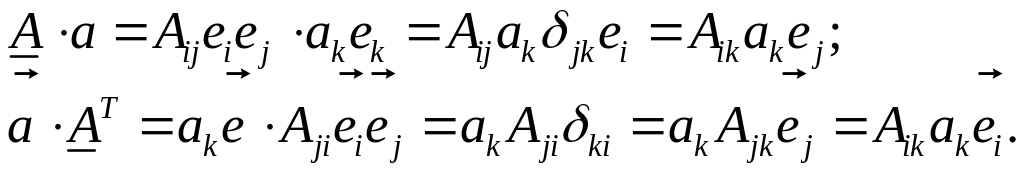
Видно, что замена строк на столбцы приводит в матрице компонент и приводит к транспонированному тензору.
Тензор называется
симметричным, если он совпадает со своим
транспонированным:
.
Это равносильно равенству
,
матрица компонент симметрична относительно
главной диагонали. Симметричный тензор
является самосопряженным.
Тензор называется
антисимметричным, если
,
т.е.
.
Очевидно, любой тензор второго ранга можно разложить на симметричную и антисимметричную части:
(1.4.8)
(1.4.9)
Пример. Тензор и его транспонированный имеют следующие компоненты в декартовом прямоугольном базисе:
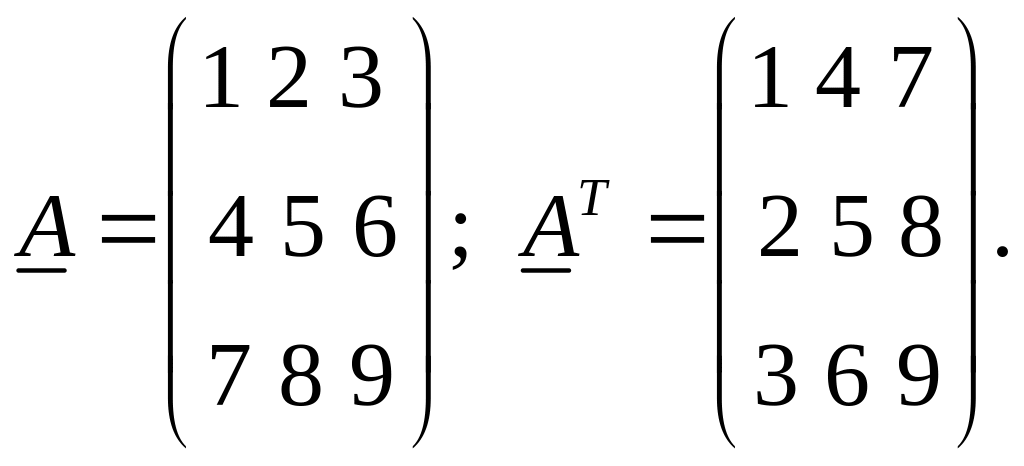
Разобьем на его симметричную и антисимметричную части:
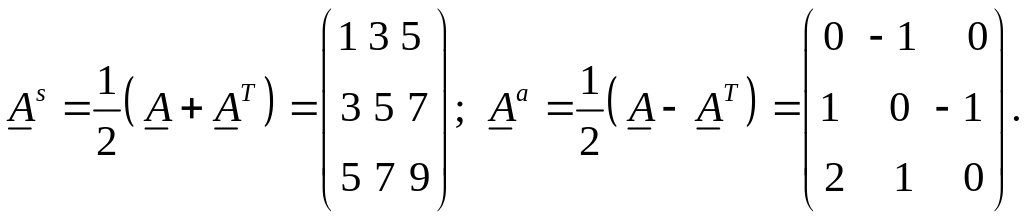
Видно, что у
симметричного тензора имеется симметрия
относительно главной диагонали, а у
антисимметричного – антисимметрия
относительно ее (кроме того, для него
на диагонали всегда находятся нули).
Легко убедиться, что
.
Замечание (о
матричном представлении тензора в
выбранном базисе). Известно, что
прямоугольная таблица элементов,
заключенная в скобки и подчиняющаяся
определенным правилам обращения с ней,
называется матрицей. Символ
обозначает элемент матрицы
,
где первый индекс – номер строки, а
второй – номер столбца. Пусть в трехмерном
евклидовом пространстве имеется
некоторый тензор и выбран какой-либо
базис, для определенности – декартов
прямоугольный, тогда любой тензор
второго ранга можно отождествить с
матрицами компонент, а вектор можно
записать либо в виде строки, либо – в
виде столбца:
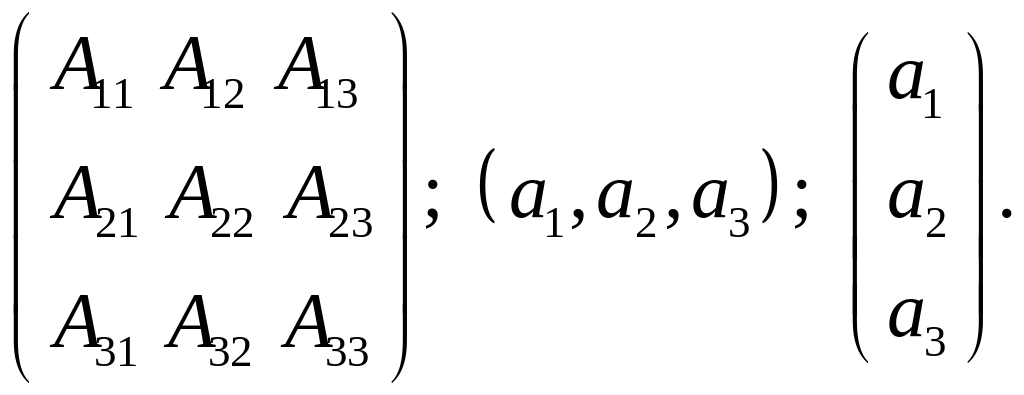
Произведение двух
матриц
соответствует произведению тензоров,
которое в индексной записи выглядит
как
.
Здесь происходит умножение по принципу
«строка на столбец».
Пример 6. Скалярное
произведение векторов
и
дает скаляр
:
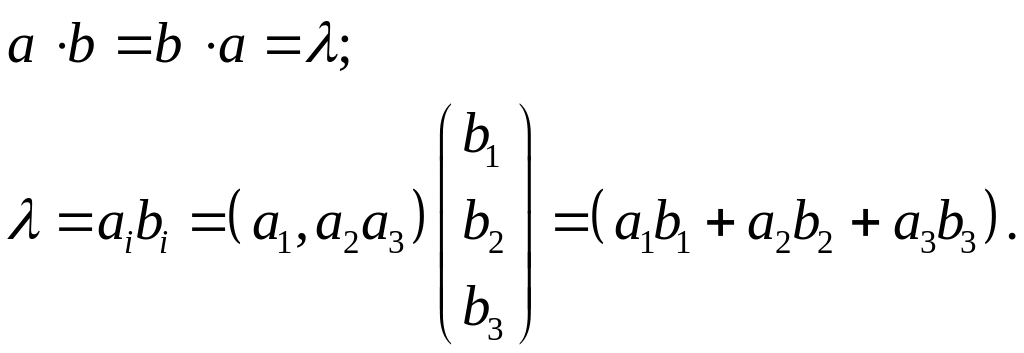
Пример 7. Скалярное произведение вектора на тензор второго ранга:
Пример 8. Скалярное произведение тензора на вектор:
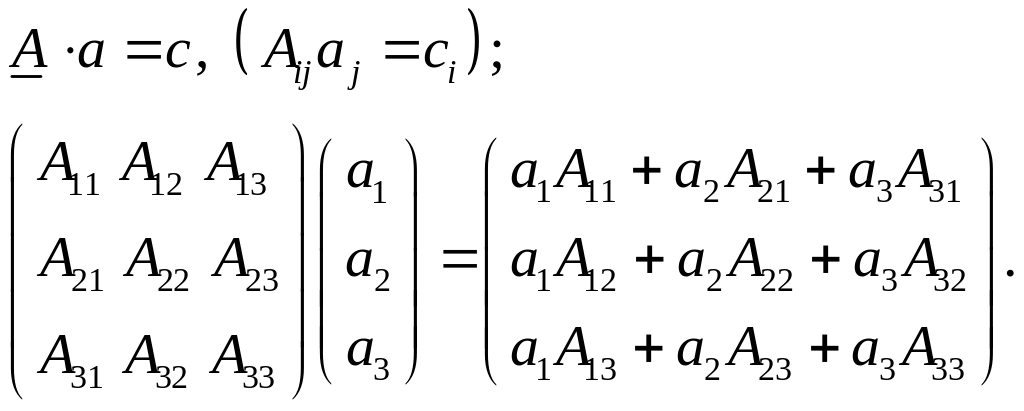
Упражнение. Пусть
в прямоугольной декартовой системе
координат вектор
имеет компоненты
,
а тензору
соответствует матрица
.
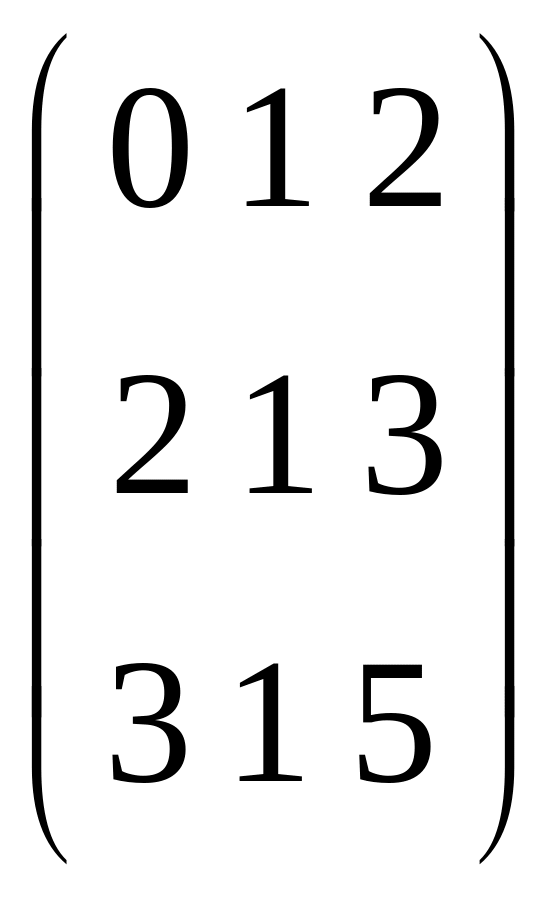Найти произведения
и
.
Операция векторного произведения векторов приводит к такому «подозрительному, зависящему от системы координат, понятию, как псевдовектор. В принципе можно не рассматривать эту операцию и тем самым не рассматривать псевдовекторы и другие псевдообъекты. Однако традиционно в механике и физике широко исаользуют операцию векторного умножения. Поэтому краткое замечание по этому поводу здесь уместно.
Рассмотрим понятие
псевдотензора, причем только в
ортонормированном базисе
.
Пусть имеется некоторая линейная
комбинация, относительно базисных
полиад
.
Если при переходе
от правой (левой) системы координат,
определяемой базисом
,
к левой (правой) системе координат,
определяемой базисом
,
компоненты
меняют знак на противоположный, а при
переходе от правой (левой) к другой
правой (левой) системе координат перемены
знака не происходит, то объект
называется псевдотензором ранга
.
Заметим, что для истинного тензора такой
перемены знака нет. Очевидно, что
псевдотензоры инвариантны по отношению
к поворотам и не инвариантны к зеркальному
отражению базиса. Псевдовектор
является частным случаем псевдотензора
– псевдотензором первого ранга.
Для обеспечения возможности записи в компонентной форме операции векторного умножения вводят специальный псевдотензор третьего ранга, так называемый альтернирующий тензор – тензор Леви-Чивита:
(1.4.10)
где компоненты
определяются следующим правилом:
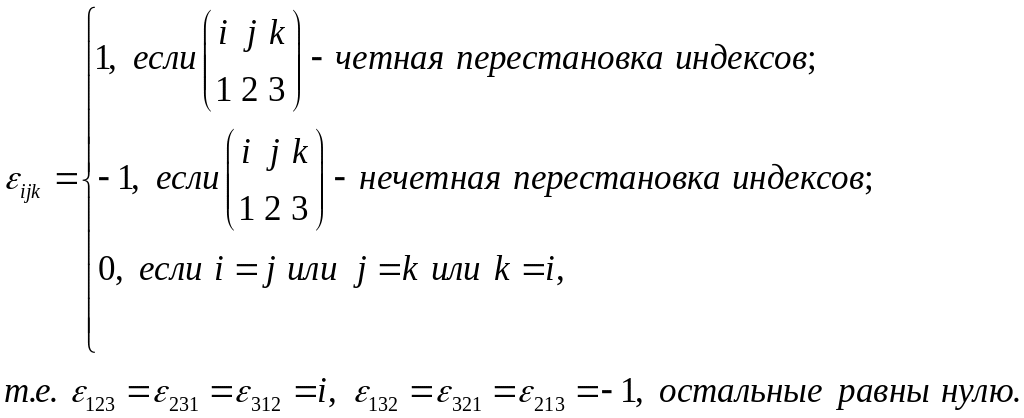(1.4.11)
Теперь можно записать векторное произведение векторов в компонентной форме. Но сначала рассмотрим векторное произведение базисных векторов. Это произведение определяется как псевдовектор
(1.4.12)
После этого определения векторное произведение двух векторов можно записать в компонентной форме следующим образом:
(
1.4.13)
Аналогичным образом можно вычислить векторное произведение тензоров. Так для тензоров второго ранга:
(1.4.14)