2.9. Формула и.С. Громеки и другие связанные с ней соотношения.

Еще одно доказательство формулы Громеко. Поскольку , то умножение этого тензора на вектор скорости справа дает:

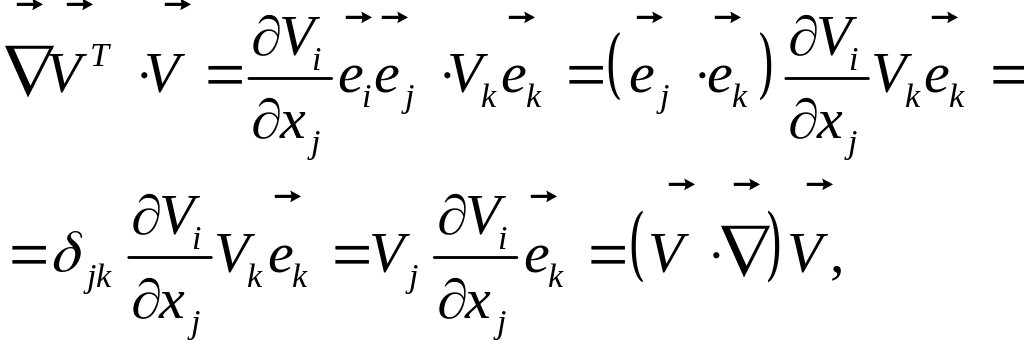(1)

т.е. получили вектор конвективного ускорения жидкой частицы. Далее выполним следующую цепочку преобразований:

(2)

Второе слагаемое можно здесь представить в виде градиента:

(3)

Первое слагаемое в правой части (2) можно записать так:

(4)

Докажем это равенство. Левая часть его:

(5)

Правая часть равенства (4) также есть вектор:

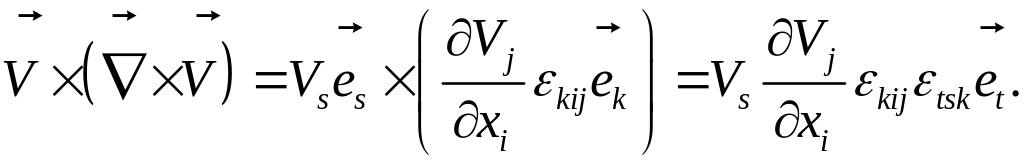(6)

Покажем, что выражения (5) и (6) эквивалентны. Для этого сравним компоненты этих векторов. В проекции на ось выражение (5) дает (полагаем ):

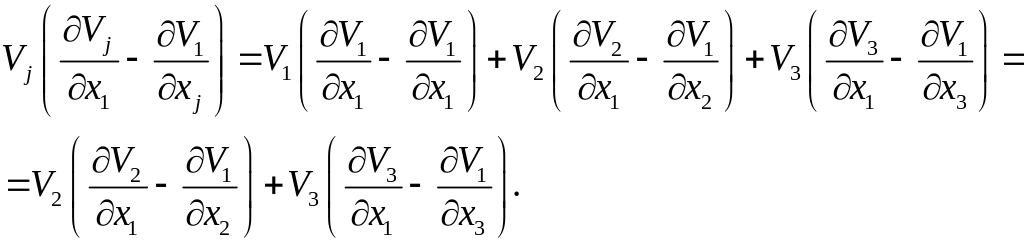
выражение (6) в проекции на эту же ось (полагаем ) дает:

Видно, что проекции на ось выражений (5) и (6) совпадают. Аналогичное совпадение имеет место и в отношении проекций на оси и .

Таким образом, соотношение (2) с учетом равенств (3) и (4) принимает вид:

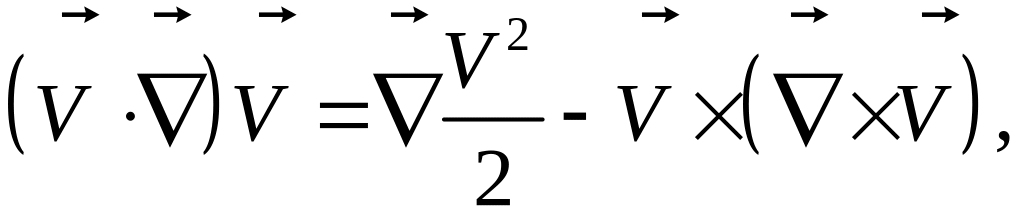(7)

а это и есть формула И.С. Громеки.

При доказательстве были получены следующие полезные формулы. Из соотношения (4) следует:

(8)

Из выражения (1):

С помощью формулы Громеки можно получить и такую:

Действительно, т.к. :

Простейшее доказательство формулы Громеки:

Преобразование компоненты при базисном векторе дает:

Аналогичным образом получаем компоненты и при других базисных векторах. В итоге имеем:

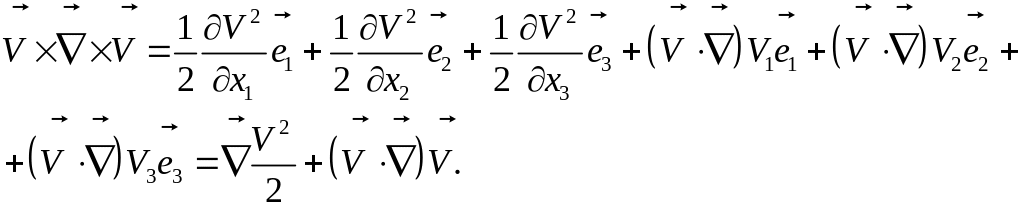
Отсюда следует формула Громеки.

Из формул (7) и (8) имеем формулу для конвективного ускорения:

вместо формулы Громеко. Кроме того полезна формула

Из сравнения правых и левых частей двух последних выражений следует:

Кроме формулы И.С. Громеки

(1)

есть и другие полезные формулы.

Так, лапласиан скорости можно представить в виде:

(2)

или, применяя устоявшиеся обозначения:

Докажем эту формулу, выполняя выкладки для :

Распишем подробнее компоненты этого вектора, стоящие у базисных векторов. При базисном векторе выражение имеет вид:

Аналогичные выкладки можно выполнить и для компонент при базисных векторах и . В итоге имеем:

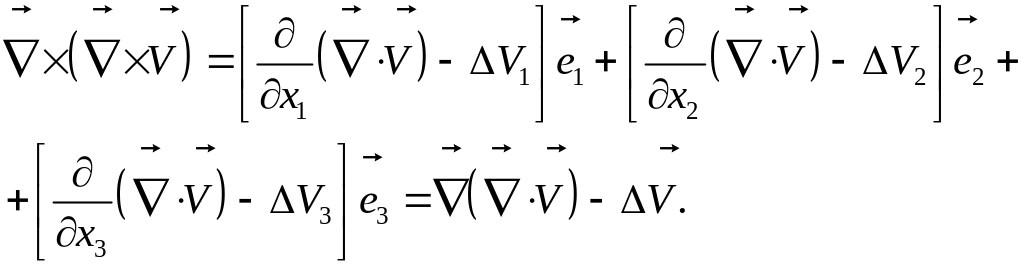
Таким образом, имеем формулу:

или

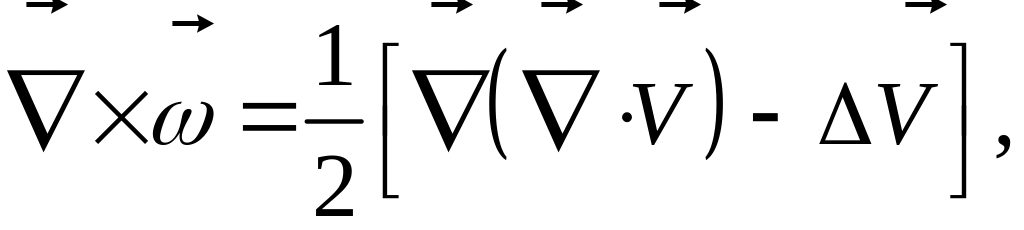
откуда и следует формула (2).

Запишем, пользуясь соотношениями (1) и (2) уравнение Навье-Стокса для стационарного течения вязкой несжимаемой жидкости в дивергентном виде. Исходное уравнение имеет вид:

(3)

Представим конвективное слагаемое по формуле Громеки (1), а лапласиан - по формуле (2) а так же учтем, что массовая сила в поле сил тяжести может быть записана через потенциал , величина , если ось направлена вертикально вверх. Тогда вместо (3) запишется:

Для несжимаемой жидкости и это выражение примет вид:

(4)

Т.е. градиент полной энергии жидкой частицы зависит от вихревой структуры потока. Если , то правая часть уравнения (4) обращается в ноль и в результате для всей области течения.

Дивергентный же вид уравнения (3) для несжимаемой жидкости можно получить, учитывая что , используя тождество (2) а так же соотношение

(5)

Тогда уравнение (3) примет форму:

(6)

Отсюда, используя понятия единичного тензора и тензора Леви-Чивита , можно записать слагаемые правой части (6) в дивергентной форме, в результате чего все уравнение Навье-Стокса в целом для установившегося течения несжимаемой жидкости принимает дивергентный вид:

(7)

Последнее слагаемое в скобках можно представить в более простом виде, учитывая, что для несжимаемой жидкости:

где - тензор скоростей деформаций.

Тогда вместо (7) будем иметь из (3):

(8)

Примечание. Сочетание формул (1) и (5) приводит к соотношению:

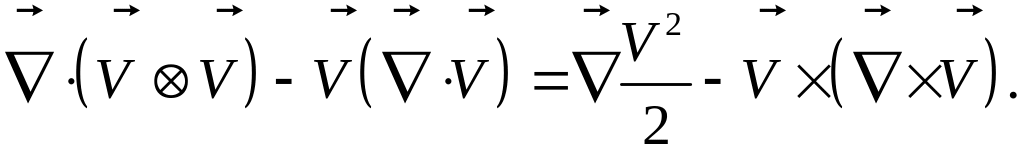
Тензор, стоящий под знаком дивергенции в квадратных скобках уравнения (8) имеет структуру тензора Лайтхилла, используемого в акустике[].

Еще одна полезная формула для течения жидкости:

которая следует из соотношения (2).