2.7. Запись уравнения энергии как скалярной величины теплоты (возможная альтернатива закону Фурье).

Уравнение энергии в современной литературе по механике жидкостей и газов [] записывают как разность балансов полной и внутренней энергии. По уравнениям переноса уравнение баланса полной энергии []:

(1)

где полная энергия движущейся частицы жидкости, включающая в себя механическую энергию и внутреннюю время; плотность; оператор материальной (Эйлеровой) производной; тензор напряжений; оператор Гамильтона (набла); скорость жидкой частицы; вектор интенсивности массовых сил (в поле сил тяжести это вектор ускорения свободного падения); вектор плотности теплового потока,

Уравнение баланса механической энергии потока получается из уравнения движения сплошной среды в напряжениях, путем скалярного умножения его на вектор После несложных преобразований это уравнение записывается в виде:

(2)

Вычитание из уравнения (1) правых и левых частей уравнения (2) дает:

(3)

Здесь двоеточие – символ двойного скалярного произведения.

Согласно этому уравнению, изменение внутренней энергии происходит за счет теплового потока (путем теплопроводности по закону теплопроводности Фурье где 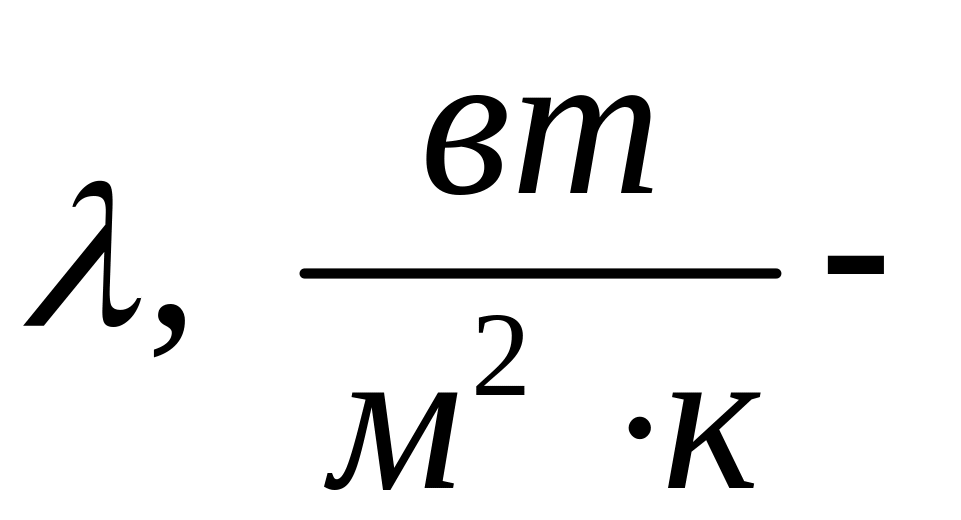коэффициент теплопроводности), а также за счет диссипации механической энергии потока жидкости, которая характеризуется слагаемым

Учитывая, что тензор напряжений вязкой жидкости может быть записан в виде:

где давление; единичный тензор; тензор вязких напряжений, а также то обстоятельство, что в правой части (3) могут быть добавлены и другие источниковые для теплоты члены, уравнение (3) в температуре обычно записывают в виде:

(4)

где интенсивность поступления к частице теплоты от действия внешних источников Это уравнение энергии в форме уравнения для переноса внутренней энергии может быть переписано и в других формах – в формах переноса энтальпии, температуры, энтропии которые являются эквивалентной исходной.

В уравнении (4) интенсивность теплового потока записывается по закону теплопроводности Фурье:

где температура; коэффициент теплопроводности, который в литературе по теплофизике обычно представляют в виде

где коэффициент температуропроводности; изобарная теплоемкость. Отсюда видно, что в уравнении (4) будет присутствовать, кроме изобарной, еще и изохорная теплоемкость поскольку, как известно из термодинамики для идеального газа, величина внутренней энергии связана с Более того, в уравнениях переноса любой физической величины (скалярной, векторной, тензорной) в правой части уравнения под знаком дивергенции должен находиться член, содержащий градиент этой величины

Здесь коэффициент, характеризующий диффузию этой величины (для поля концентрации – это коэффициент диффузии , для поля скоростей – это кинематическая вязкость и так далее.). Однако, в уравнении (4) члена под знаком дивергенции нет, поскольку закон теплопроводности Фурье не предполагает его наличия. Положение несколько исправляется, если уравнение энергии записать в виде уравнения для переноса энтальпии когда для газов и закон теплопроводности Фурье записывается в виде:

а уравнение энергии приобретает вид:

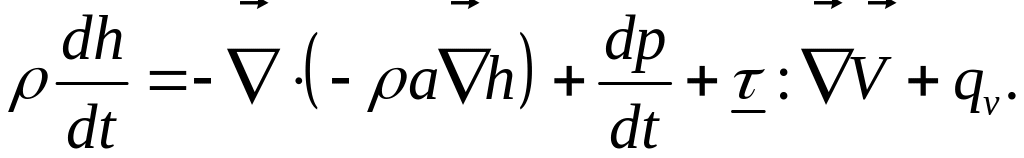(5)

Можно получить уравнение энергии и в другой, альтернативной общепринятой форме, непосредственно используя первый закон термодинамики, согласно которого изменение теплоты связано с изменением внутренней энергии и совершением работы

(6)

Для простых термодинамических систем этой работой является работа расширения в случае сложных – добавляется, например, работа сил поверхностного напряжения, или же система является необратимой, то сюда может входить и работа сил трения.

Поэтому запишем равенство (6) в виде:

(7)

где работа, дополнительная к работе расширения.

Для уравнения переноса возьмем в качестве исходной величину Запишем уравнение переноса для этой скалярной величины, сопоставив ей векторную интенсивность, плотность переноса теплоты

(8)

где плотность; температуропроводность, знак минус означает, что вектор теплового потока направлен в сторону областей с меньшей теплотой.

Уравнение (8) является определяющим для теплового потока, его можно рассматривать как альтернативу уравнению Фурье.

Для потока идеального газа можно записать уравнение теплового баланса:

которое означает, что изменение теплоты равно притоку (оттоку) тепла вследствие теплопроводности. Если же кроме теплопроводности имеются и другие механизмы изменения теплоты, например диссипативные (по Рэлею), то их надо учесть. В итоге, с учетом формулы (8), имеем:

(9)

где другие источники теплоты.

Обычно в современной теории теплопередачи чаще всего используют вариант с пренебрежением диссипативного слагаемого, а также во многих случаях Тогда:

(10)

Рассмотрим приложение этого уравнения к течениям совершенного газа (идеального с постоянным значениями и по молекулярно-кинетической теории газов). Такие течения наиболее интенсивны с позиций газовой динамики. Для каждого типа термодинамического процесса определяющее соотношение – аналог (8) для закона теплопроводности Фурье – будет свое, разными будут и конкретизации уравнения энергии.

Для изохорного процесса как известно вся подводимая теплота расходуется на изменение внутренней энергии, то есть:

Но для совершенного газа откуда следует, что плотность теплового потока

(11)

а уравнение (10) принимает вид:

или, после подстановки и для жидкости с постоянными физическими свойствами:

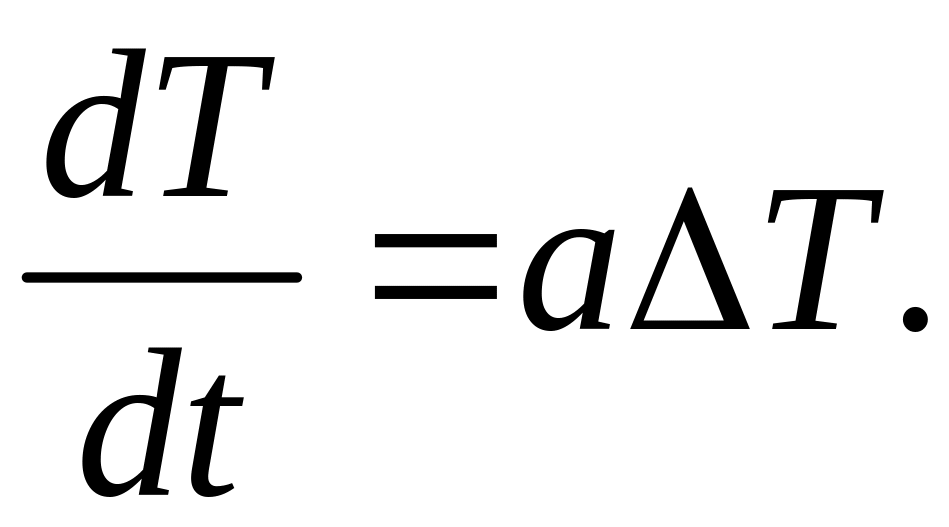(12)

Это выражение совпадает с известным в теплопередаче уравнением для переноса температуры.

Для изобарного процесса вся теплота расходуется на изменение энтальпии, то есть:

Тогда, учитывая что имеем для плотности потока тепла:

а уравнение энергии (10) для жидкости с постоянными физическими свойствами приобретает вид (после сокращения на :

(13)

Видно, что уравнения (12) и (13) совпадают.

Для изотермического процесса подводимая теплота расходуется на совершение работы расширения:

Тогда тепловой поток, в соответствии с (8):

и уравнение энергии принимает вид:

Или, после несложных преобразований, полагая

Для адиабатного процесса и перемещения теплоты в пространстве не происходит, уравнение (10) превращается в тождество

А теперь рассмотрим случай произвольного термодинамического процесса – политропного с показателем политропы Теплоемкость его уравнение процесса Подводимая теплота в этом процессе расходуется как на изменение внутренней энергии, так и на совершение работы расширения:

Учитывая, что в терминах энтальпии имеем:

(14)

Тогда:

и формула (8) приобретает вид:

(15)

Уравнение (10) при постоянных физических свойствах принимает вид:

(16)

Если эффекты, связанные с изменением давления малы, ими можно пренебречь, то получаем:

(17)

что совпадает с уравнениями (12) и (13).

Замечание: если для политропного процесса записать то

и уравнение энергии :

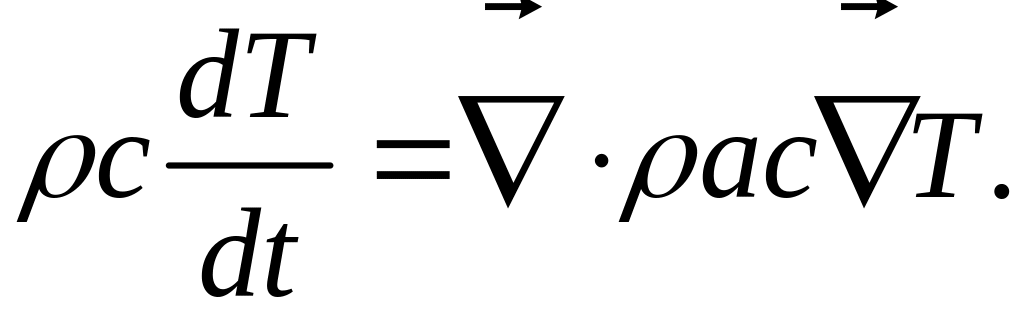(18)

При постоянных физических свойствах это уравнение совпадает с (17).

Замечание: сравнение выражений для

дает связь и

Вычислим производную для этого процесса.

Для политропного процесса совершенного газа одновременно выполняется система уравнений, состоящая из уравнения Менделеева-Клайперона и уравнения политропы:

Отсюда можно выразить величину через и найти нужную производную Так как из первого уравнения этой системы то подстановка во второе дает:

Тогда:

В итоге имеем для теплоемкости в политропном процессе:

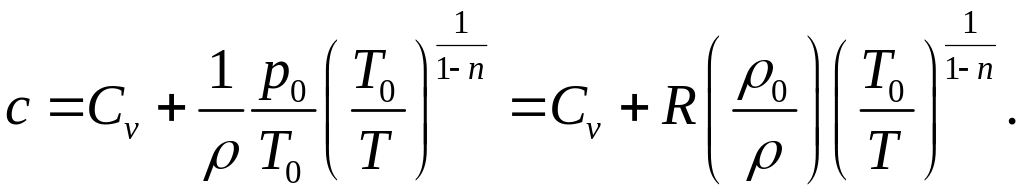
В начальной точке процесса, где имеем, согласно формулы Майера:

а далее в ходе процесса теплоемкость изменяется в зависимости от его вида.

В случае, если теплота переносится не только теплопроводностью, но имеются другие источники ее, необходимо опираться на уравнение (9). Видно, что закон теплопроводности и уравнение энергии зависит от вида процесса.