
- •Інститут економіки та нових технологій Кафедра прикладної математики та математичного моделювання
- •Наклад 200 примірників Передмова
- •І. Основні питання, що вивчаються в розділі „Ряди”
- •Означення числового ряду. Збіжні та розбіжні числові ряди.
- •Іі. Основні теоретичні відомості. Приклади розв’язання задач
- •1. Означення числового ряду. Збіжні та розбіжні числові ряди
- •3.1. Ознака порівняння.
- •Теорема 4 (ознака порівняння в граничній формі)
- •3.2. Ознака Даламбера
- •3.3. Радикальна ознака Коші
- •3.4. Інтегральна ознака Коші
- •4. Числові ряди з довільними членами. Умовна та абсолютна збіжності
- •Приклад 17
- •Розв’язання
- •6. Функціональні ряди. Область збіжності функціонального ряду
- •Приклад 18
- •Розв’язання
- •8. Використання степеневих рядів для наближених обчислень Приклад 21
- •Розв’язання
- •Приклади 22-23
- •Розв’язання
- •Розв’язання
- •Ііі. Завдання для самостійної роботи
- •IV. Завдання для контрольної роботи Завдання 1
- •Варіанти завдань:
- •Завдання 2
- •Варіанти завдань:
- •Завдання 3
- •Варіанти завдань:
- •Завдання 4
- •Варіанти завдань:
- •Завдання 5
- •Варіанти завдань:
- •Завдання 6
- •Варіанти завдань:
- •Завдання 7
- •Варіанти завдань:
- •Завдання 8
- •Варіанти завдань:
- •Завдання 9
- •Варіанти завдань:
- •V. Список використаної і рекомендованої літератури
8. Використання степеневих рядів для наближених обчислень Приклад 21
Користуючись
розкладом підінтегральної функції в
степеневий ряд, обчислити вказаний
визначений інтеграл з точністю до 0,001:
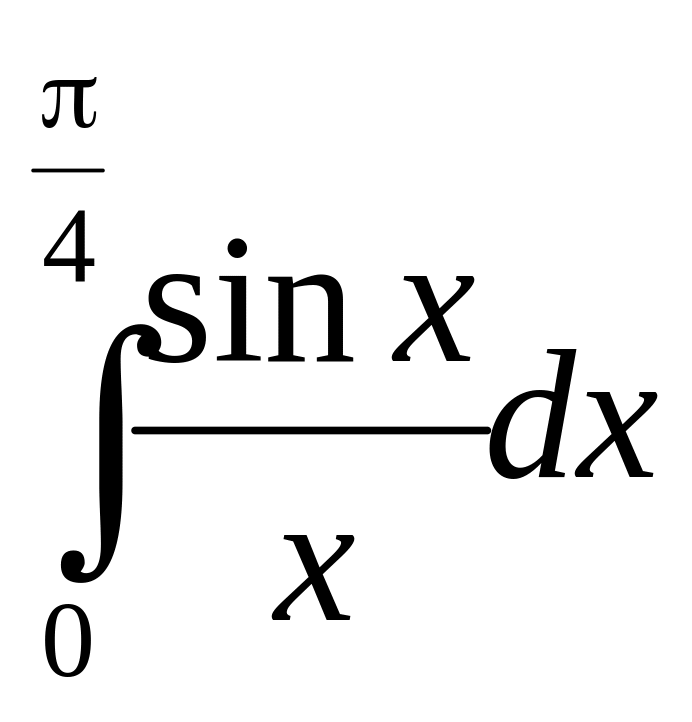 .
.
Розв’язання
Знайдемо розклад підінтегральної функції в степеневий ряд:
![]() ,
тоді
,
тоді
![]()
Оскільки межі інтегрування належать інтервалу збіжності цього ряду, наближене обчислення інтегралу можна здійснити з наперед заданою точністю.
Інтегруючи
цей ряд почленно, маємо:
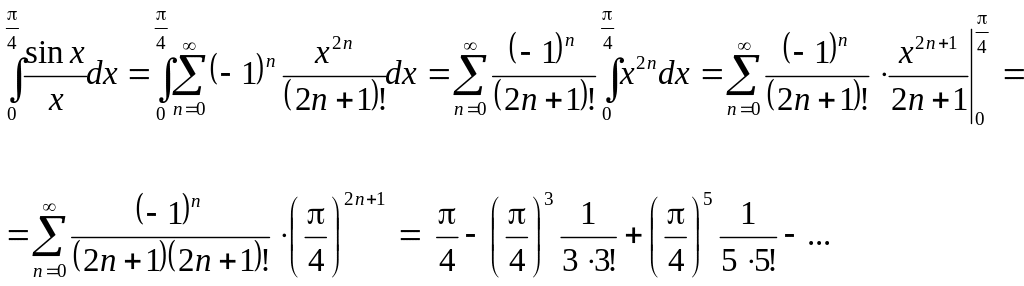
Отриманий
числовий ряд є рядом Лейбніца. Похибка,
отримана при відкиданні всіх членів
ряду, починаючи з третього, за абсолютною
величиною буде менша від третього члена:
![]() .
.
Обчислюючи
з точністю до 0,001, маємо:
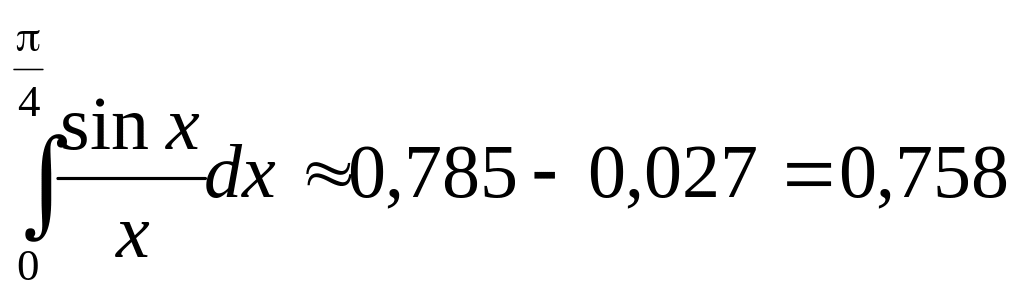 .
.
Приклади 22-23
Знайти розклад у степеневий ряд по степенях х розв’язок диференціального рівняння.
22.
![]()
![]()
Розв’язання
Розв’язок
![]() будемо шукати у вигляді ряду Тейлора:
будемо шукати у вигляді ряду Тейлора:
![]()
Оскільки
в нашій задачі
![]() ,
отримаємо розв’язок у вигляді:
,
отримаємо розв’язок у вигляді:
![]() .
.
Знайдемо
коефіцієнти степеневого ряду. Підставляючи
в диференціальне рівняння початкові
умови, отримуємо, що
![]() .
Продиференціювавши рівняння, знаходимо:
.
Продиференціювавши рівняння, знаходимо:
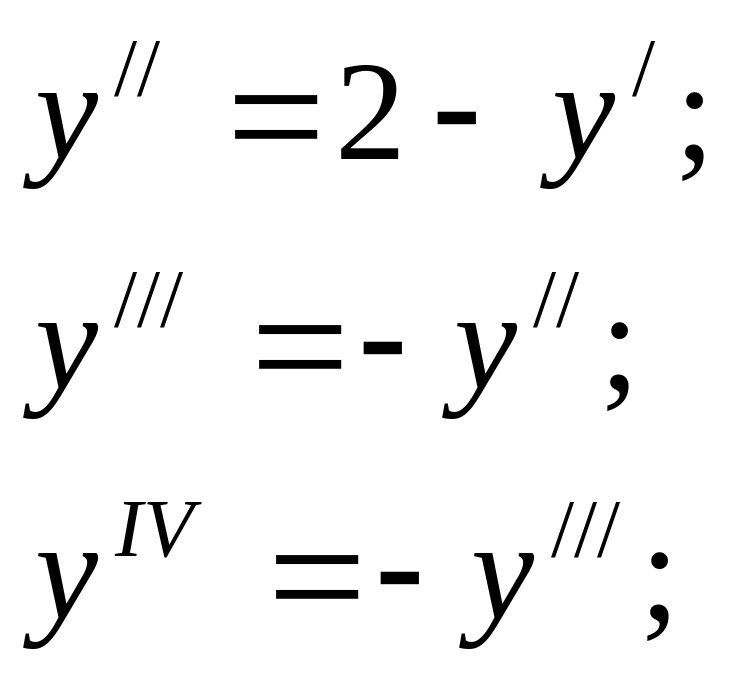

Таким чином:

Використавши
перетворення та розклад у степеневий
ряд функції
![]() ,
маємо:
,
маємо:
![]() .
.
23.
![]()
![]()
![]() .
.
Розв’язання
Розв’язок
диференціального рівняння матиме
вигляд:
![]()
Знаходимо коефіцієнти степеневого ряду:
![]() ,
,![]() ,
,
![]() ;
;
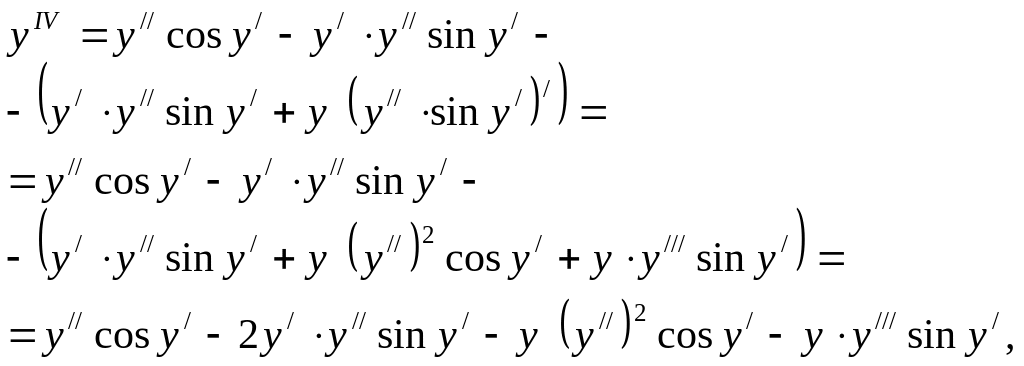
![]() .
.
Таким чином,
![]()
Ііі. Завдання для самостійної роботи
Довести збіжність ряду за означенням і знайти його суму:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Дослідити на збіжність ряди:
а)
![]() ; б)
; б)
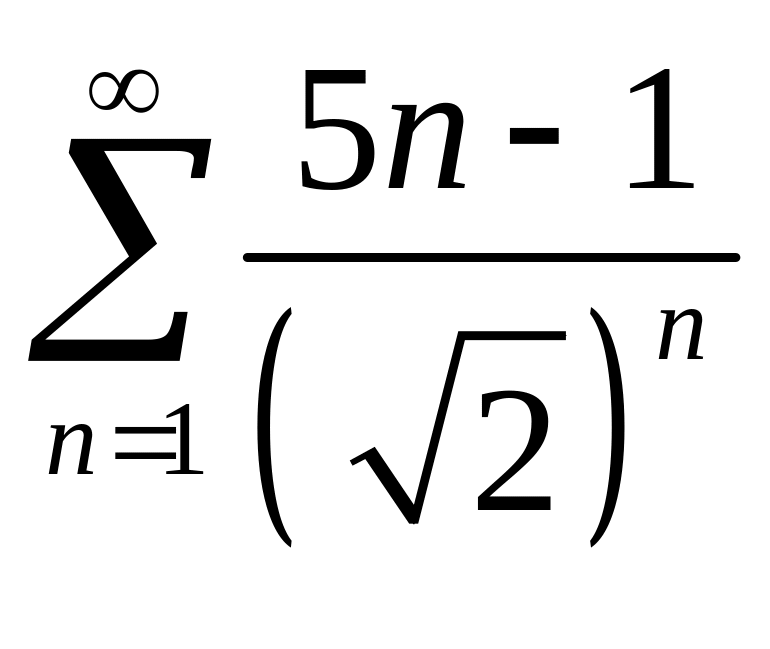 ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
є)
![]() ;
ж)
;
ж)
 ;
з)
;
з)
![]() .
.
За допомогою інтегральної ознаки Коші дослідити на збіжність ряди:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дослідити на умовну та абсолютну збіжність ряди:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
є)
![]() ;
ж)
;
ж)
![]() ;
;
з)
![]() .
.
Знайти суму ряду
 з похибкою до
з похибкою до
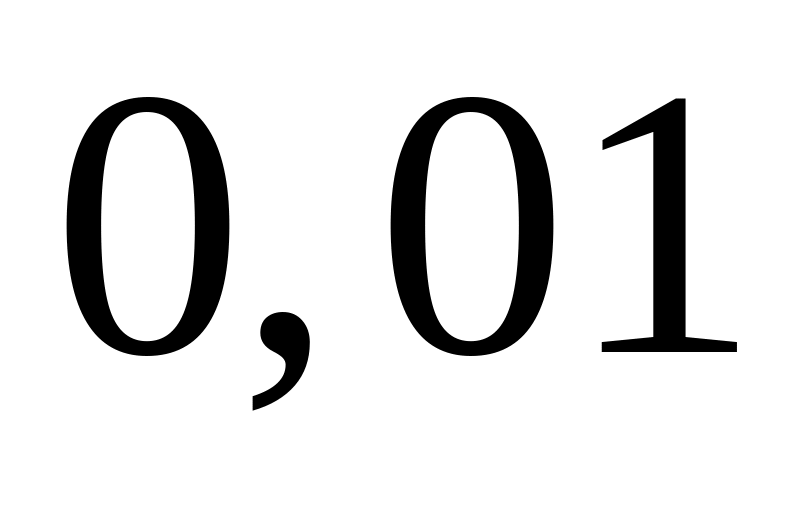 .
.Скільки перших членів ряду
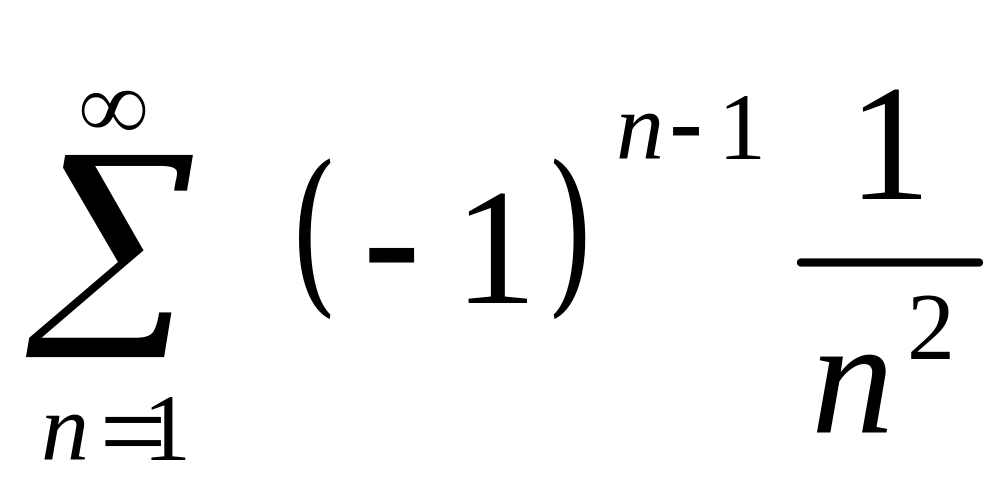 потрібно взяти, щоб їх сума відрізнялась
від суми ряду на величину, меншу, ніж
потрібно взяти, щоб їх сума відрізнялась
від суми ряду на величину, меншу, ніж
 .
.
Знайти область збіжності функціонального ряду.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обчислити визначений інтеграл з точністю до 0,001, використавши розклад підінтегральної функції в ряд.
![]()
![]()
![]()
![]()
Знайти розклад в степеневий ряд розв’язок диференціального рівняння:
![]()
![]()
![]()
![]()
IV. Завдання для контрольної роботи Завдання 1
Дослідити збіжність ряду, скориставшись означенням, та знайти його суму, якщо він збігається.
Варіанти завдань:
1.
![]() ;
2.
;
2.
![]() ;
;
3.
![]() ;
4.
;
4.
![]() ;
;
5.
![]() ;
6.
;
6.
![]() ;
;
7.
![]() ;
8.
;
8.
![]() ;
;
9.
![]() ;
10.
;
10.![]() ;
;
11.
![]() ;
12.
;
12.
![]() ;
;
13.
![]() ;
14.
;
14.
![]() ;
;
15.
![]() ;
16.
;
16.
![]() ;
;
17.
![]() ;
18.
;
18.
![]() ;
;
19.
![]() ;
20.
;
20.
![]() ;
;
21.
![]() ;
22.
;
22.
![]() ;
;
23.
![]() ;
24.
;
24.
![]() ;
;
25.
![]() ;
26.
;
26.
![]() ;
;
27.
![]() ;
28.
;
28.
![]() ;
;
29.
![]() ;
30.
;
30.
![]() ;
31.
;
31.![]() 32.
32.
![]()
33.
;
34.
![]()
