3.1. Ознака порівняння.

Теорема 3

Якщо для двох рядів (1) та (2) і для всіх ( – деяке натуральне число) виконуються нерівності , то із розбіжності першого ряду випливає розбіжність другого, а із збіжності другого – збіжність першого.

Зауваження. Якщо при порівнянні рядів (1) і (2) нерівності виконуються для всіх їх членів, то ознаки порівняння можна сформулювати так: якщо розбігається ряд із менших членів, то із більших теж; якщо збігається ряд із більших членів, то із менших також.

При дослідженні на збіжність рядів за допомогою ознак порівняння слід мати деякі "еталонні" ряди, поводження яких відоме. До таких "еталонних" рядів належать узагальнені гармонічні ряди , які збігаються при і розбігаються при , та сума членів нескінченної геометричної прогресії , яка збігається при .

Приклад 5

Дослідити збіжність ряду .

Розв’язання

Враховуючи нерівність , і порівнюючи даний ряд із геометричною прогресією , знаменник якої , переконуємося, що за ознакою порівняння заданий ряд збігається.

Теорема 4 (ознака порівняння в граничній формі)

Якщо для двох рядів з додатними членами і виконується умова , де – будь-яке число, не рівне нулю, то обидва ряди поводять себе однаково: або збігаються, або розбігаються.

Приклад 6

Дослідити збіжність ряду .

Розв’язання

За еталон беремо ряд . Він збігається як сума членів геометричної прогресії зі знаменником .

Обчисливши границю , робимо висновок, що даний ряд збіжний.

Приклад 7

Дослідити збіжність ряду .

Розв’язання

Скористаємося ознакою порівняння в граничній формі. За умовою . Для порівняння візьмемо гармонічний розбіжний ряд із загальним членом .

Обчислимо границю:

. Вихідний ряд розбігається.

3.2. Ознака Даламбера

Теорема 5 (Даламбера)

Якщо в ряді , , (починаючи з деякого номера ) існує границя , то:

1. при ряд збігається;

2. при ряд розбігається;

3. при потрібні додаткові дослідження.

Приклад 8

Дослідити збіжність ряду .

Розв’язання

Оскільки , то .

Обчислимо границю: .

Отже, заданий ряд розбіжний за ознакою Даламбера.

3.3. Радикальна ознака Коші

Теорема 6

Якщо в ряді , починаючи з деякого номера , , існує границя , то:

1. при ряд (1.1) збігається;

2. при ряд розбігається;

3. при потрібні додаткові дослідження.

Приклад 9

Дослідити на збіжність ряд .

Розв’язання

Обчислимо границю

. Робимо висновок, що ряд збігається за радикальною ознакою Коші.

Приклад 10

Дослідити на збіжність ряд .

Розв’язання.

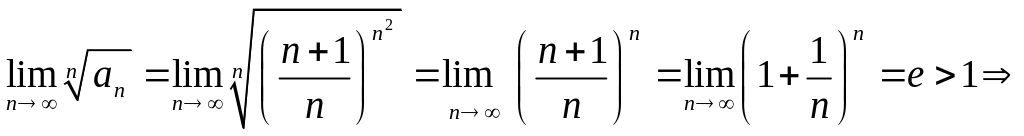
даний ряд розбігається.

3.4. Інтегральна ознака Коші

Теорема 7

Якщо члени ряду (1.1) монотонно спадають і існує функція , неперервна при , така, що , то ряд (1.1) і невласний інтеграл одночасно збігаються або розбігаються.

Приклад 11

Дослідити на збіжність узагальнений гармонічний ряд , який раніше рекомендували як "еталон" до ознак порівняння.

Розв’язання

Обчислимо відповідний йому невласний інтеграл:

Одержаний результат показує, що інтеграл, а значить і узагальнений гармонічний ряд збігається при і розбігається при .

Приклад 12

Дослідити ряд на збіжність, скориставшись інтегральною ознакою Коші: .

Розв’язання

Функція додатна, неперервна, монотонно спадна при . При натуральних значеннях аргументу її значення збігаються з відповідними членами ряду.

Обчислимо: :

.

Висновок: невласний інтеграл і досліджуваний ряд розбіжні.

Приклад 13

Дослідити збіжність ряду .

Розв’язання

Скористаємось інтегральною ознакою Коші. Для цього дослідимо невласний інтеграл:

.

Тобто невласний інтеграл і досліджуваний ряд збіжні.