6. Функціональні ряди. Область збіжності функціонального ряду

Ряди (6.1), членами яких є не числа, а функції, визначені в деякій області визначення аргументу х, називають функціональними.

Для кожного значення х₀ з області визначення функцій функціональний ряд перетворюється в числовий ряд:

. (6.2)

Якщо цей ряд збіжний, точку х₀ називають точкою збіжності функціонального ряду. Множину всіх точок збіжності функціонального ряду називають його областю збіжності.

Степеневим рядом є функціональний ряд, який має вигляд:

(6.3),

де а – стала, – числа, що мають назву коефіцієнтів степеневого ряду.

Якщо , степеневий ряд набуває вигляду:

. (6.4)

Степеневий ряд завжди збіжний при .

Якщо ряд збігається в точці , тоді існує число , таке, що для всіх степеневий ряд збігається, для всіх – розбігається. Інтервал називають інтервалом збіжності, а половину його довжини, число R – радіусом збіжності.

Областю збіжності степеневого ряду є інтервал , до якого, залежно від конкретних випадків, можна додати кінцеві точки та . В кожній точці інтервалу ряд збігається абсолютно. Якщо степеневий ряд збігається для всіх значень х, вважають , якщо ж він збігається тільки для , вважають .

Інтервал збіжності можна знаходити, застосовуючи ознаку Даламбера, або ознаку Коші до ряду, складеного з абсолютних величин членів вихідного ряду.

Записавши ряд (6.3) у вигляді:

, (6.5)

та розглянувши ряд, складений з абсолютних значень членів ряду (6.5), який має вигляд:

, (6.6)

знаходять інтервал збіжності з нерівностей: (6.7) або (6.8)

Приклад 18

Знайти область збіжності ряду .

Розв’язання

Застосуємо ознаку Даламбера: ;

.

Знайдемо значення х, для яких виконується нерівність

, – область збіжності ряду.

Тоді радіус збіжності R=3.

Перевіримо, чи збігається ряд якщо :

1. Якщо , отримаємо числовий ряд .

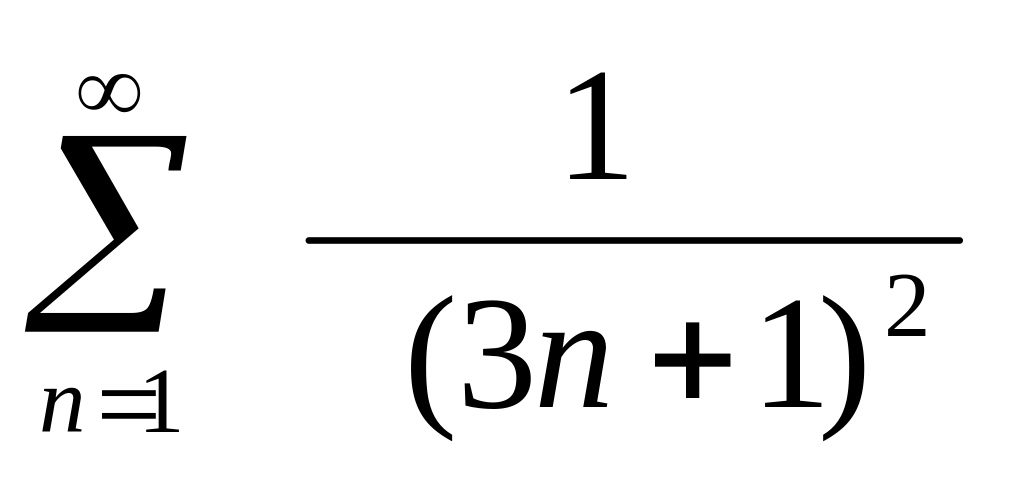Порівняємо даний ряд із збіжним рядом :

.

Отже, ряд також збігається;

2. Якщо , маємо ряд , який (як ми вже знаємо) збігається.

Отже, та входять до області збіжності .

Приклад 19

Знайти область збіжності ряду

Розв’язання

Згідно з ознакою Даламбера маємо:

, , тоді

Ця нерівність правильна для всіх значень х. Отже, область збіжності , радіус збіжності R = .

Приклад 20

Знайти область збіжності ряду .

Розв’язання

Використаємо ознаку Коші. Знайдемо .

Зрозуміло, що умова виконується тільки якщо х=5, тобто ряд збігається якщо х=5, тоді радіус збіжності R=0.

7. Розклад функцій в степеневі ряди. Ряд Тейлора

Якщо функція f (x) в деякому інтервалі, що містить точку а, має похідні всіх порядків, тоді для неї можна застосувати формулу Тейлора.

(7.1)

де ( а с х, n ) – залишковий член ряду.

Якщо в цьому ж інтервалі виконується умова , тоді функцію можна розкласти в ряд Тейлора для значення х, що розглядається:

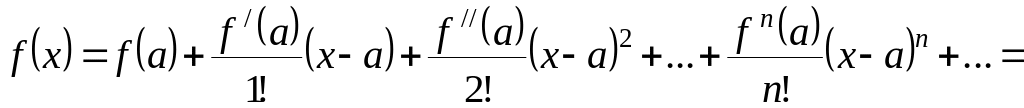
(7.2)

Якщо а = 0 , отримаємо ряд Маклорена:

(7.3)

Для виключення процесу багаторазового диференціювання при розкладанні деяких функцій в ряд Тейлора можна використовувати готові розклади основних елементарних функцій з комбінуванням правил додавання, віднімання та множення рядів.

Наведемо розклади в ряд Маклорена основних функцій.

(7.4)

(7.5)

( 7.6)

(7.7)

(7.8) (7.9)

. (7.10)