4. Числові ряди з довільними членами. Умовна та абсолютна збіжності

Означення 4. Числовий ряд , члени якого після будь-якого номера мають різні знаки, називається рядом із довільним розподілом знаків або рядом із довільними членами.

Мова йде про ряди типу , в яких знаки можуть певним чином залежати від номера .

Означення 5. Збіжність ряду (1.1) називається абсолютною, якщо збігається ряд і умовною, якщо ряд розбігається.

Приклад 14

Дослідити збіжність ряду .

Розв'язання

Цей ряд має члени з вільним розподілом знаків. Розглянемо ряд із модулів членів досліджуваного ряду: 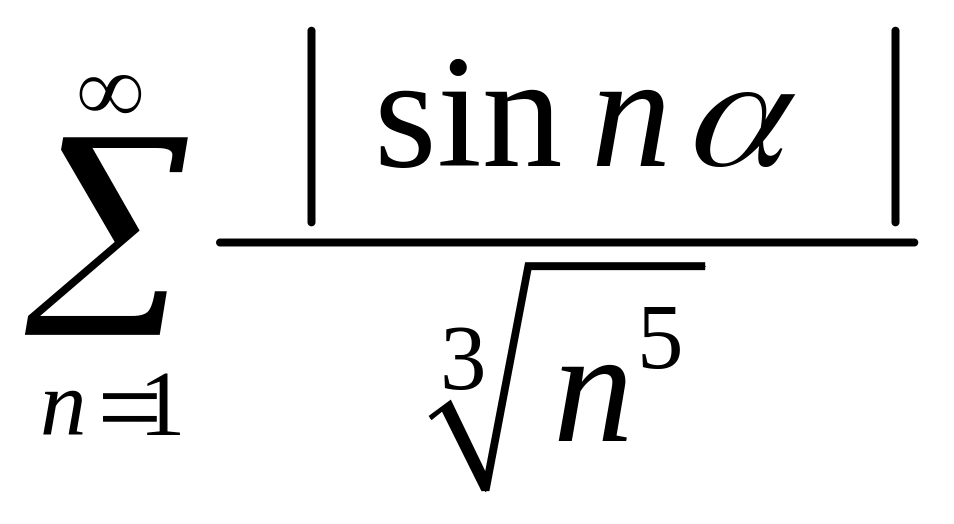. Застосуємо до нього ознаку порівняння, маючи на увазі, що .

Оскільки ряд збігається, то збігається також ряд , а, значить, досліджуваний ряд збігається абсолютно.

Зауваження. Збіжність ряду є достатньою ознакою збіжності рядів із вільним розподілом знаків.

5. Знакопереміжні ряди. Теорема Лейбніца

Означення 6. Знакопереміжним називається ряд, який має такий вигляд: , де (5.1)

Знакопереміжний ряд є окремим випадком числового ряду з довільними членами.

Теорема 7 (Ознака Лейбніца)

Якщо в ряді (5.1) члени за модулем монотонно спадають і , то він збігається, причому його сума за модулем не перевищує абсолютної величини першого члена, а залишок його за модулем не перевершує абсолютної величини першого відкинутого члена.

Приклад 15

Дослідити на абсолютну і умовну збіжність ряд .

Розв'язання

Оскільки члени даного знакопереміжного ряду монотонно спадають і , тому за ознакою Лейбніца досліджуваний ряд збігається. Розглянемо ряд із модулів його членів .

Застосуємо до нього інтегральну ознаку Коші. Загальний член ряду задамо функцією при .

Обчислимо:

Отже, ряд із модулів розходиться, а значить, досліджуваний ряд збігається умовно.

Приклад 16

Дослідити на абсолютну і умовну збіжність ряд .

Розв’язання

Даний ряд – знакопереміжний. Він задовольняє умовам теореми Лейбніца: його члени за абсолютною величиною спадають, коли зростає, і, крім того, .

Таким чином, цей ряд за теоремою Лейбніца збігається. З'ясуємо тепер, як збігається даний ряд: абсолютно чи умовно. Для цього розглянемо ряд із модулів членів досліджуваного ряду: . Враховуючи, що при , а ряд розбіжний, робимо висновок, що ряд також розбігається. Таким чином, даний ряд збігається умовно.

Дуже важливим для наближених обчислень є твердження в теоремі Лейбніца про те, що залишок за модулем не перевершує модуля свого першого члена.

Приклад 17

Знайти наближено суму ряду із точністю до .

Розв’язання

Оскільки даний ряд – знакопереміжний, збіжний то величина відкинутого при обчисленні залишку ряду, який також є знакопереміжним рядом, не перевищує модуля свого першого члена (на основі зауваження 2 до ознаки Лейбніца). Потрібне число визначимо шляхом підбору із нерівності . При остання нерівність виконується. Тобто, якщо відкинути в даному ряді всі члени, починаючи з шостого, то похибка за модулем не перевершує модуля шостого члена. Отже, знайдемо наближено суму даного ряду, замінивши її частковою сумою шести перших членів. Маємо:

.