Інститут економіки та нових технологій Кафедра прикладної математики та математичного моделювання

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

до самостійного вивчення вищої математики

на економічному факультеті

Розділ IX. Ряди

I курс, 2 семестр.

Кременчук

2004

Розповсюдження і тиражування без офіційного дозволу ІЕНТ і авторів заборонено.

Методичні рекомендації до самостійного вивчення вищої математики на економічному факультеті

(Розділ IX. Ряди. I курс, 2 семестр).

Укладач: Тристан Віктор Миколайович, старший викладач.

Рецензент: Семенов В.О, кандидат фізико-математичних наук, професор.

Комп’ютерна верстка: Тристан А.В.

Відповідальний за випуск: професор Семенов В.О.

Методичні рекомендації розглянуті та рекомендовані до видання на засіданні кафедри прикладної математики та математичного моделювання від 30 серпня 2003р., протокол № 1

Схвалено методичною радою ІЕНТ “_____”_______________р.,

протокол №______.

Затверджено Вченою радою ІЕНТ “_____”_______________р.,

протокол №______.

Наклад 200 примірників Передмова

Методичні рекомендації адресовані студентам економічного факультету, які навчаються за спеціальностями „Облік і аудит” і „Маркетинг” стаціонарно та заочно. Вони містять необхідний теоретичний матеріал і розв’язання типових задач ІХ розділу курсу вищої математики „Ряди”, що вивчається в другому семестрі.

Мета методичних рекомендацій полягає у тому, щоб допомогти студентам засвоїти цей розділ курсу вищої математики та набути навичок самостійної роботи при розв’язуванні задач.

Методичні рекомендації містять завдання для самостійної роботи, завдання контрольної роботи в 34 варіантах .

З метою самоконтролю за вивченням курсу до методичних рекомендацій внесено питання для підготовки до екзамену.

Методичні вказівки містять список рекомендованої літератури.

І. Основні питання, що вивчаються в розділі „Ряди”

1. Означення числового ряду. Збіжні та розбіжні числові ряди.

2. Необхідна ознака збіжності та достатня ознака розбіжності.

3. Ряди з додатними членами та ознаки їх збіжності.

   1. Ознаки порівняння;

   2. Ознака Даламбера;

   3. Радикальна ознака Коші;

   4. Інтегральна ознака Коші.

4. Числові ряди з довільними членами. Умовна та абсолютна збіжності.

5. Знакопереміжні ряди. Ознака Лейбніца.

6. Функціональні ряди. Область збіжності.

7. Розклад функцій в степеневі ряди. Ряди Тейлора і Маклорена.

8. Використання рядів для наближених обчислень.

Іі. Основні теоретичні відомості. Приклади розв’язання задач

1. Означення числового ряду. Збіжні та розбіжні числові ряди

Означення 1. Числовим рядом називається вираз , де . (1.1)

Числа називаються членами ряду, а число – загальним членом ряду.

Числові ряди поділяються на ряди із знакосталими членами та ряди з довільним розподілом знаків. Для знакосталого ряду всі його члени мають бути недоданими або невід’ємними числами.

Означення 2. Суми , називаються частковими сумами ряду.

Часткові суми утворюють послідовність , .

Означення 3. Числовий ряд (1.1) називається збіжним, якщо існує границя , а число – є його сумою. Якщо ж границя не існує (зокрема нескінченна), то ряд (1.1) називається розбіжним.

Факти збіжності та розбіжності ряду надалі будемо коротко позначати відповідно символами та .

Сума називається -м залишком ряду (1.1).

Якщо ряд (1.1) збігається, то .

Приклад 1

Дослідити збіжність ряду за означенням та знайти його суму, якщо ряд збігається.

Розв’язання

Запишемо -у часткову суму даного ряду і перетворимо її:

Обчислимо: .

Це означає, що ряд збігається і має суму .

Приклад 2

Дослідити збіжність ряду

(1.2)

Цей ряд являє собою суму членів геометричної прогресії зі знаменником , яка збігається при , і сума ряду (1.2) обчислюється за формулою .

Якщо , то ряд (1.2) розбігається.

Приклад 3

Довести збіжність ряду і знайти його суму, якщо ряд збігається.

Розв’язання

Загальний член даного ряду подамо у вигляді суми найпростіших дробів.

, , , .

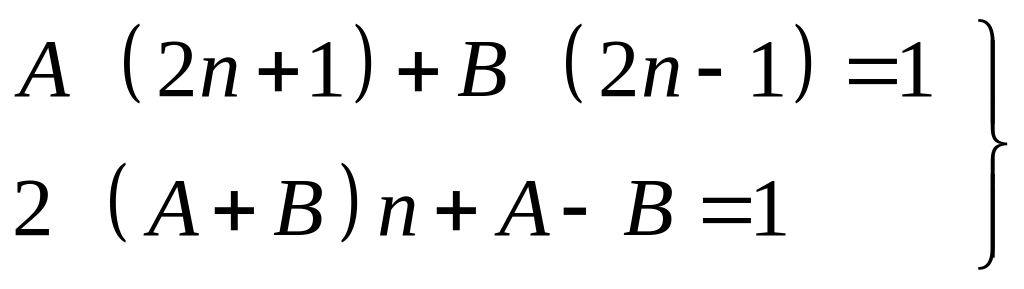Отже, .

Знаходимо :

.

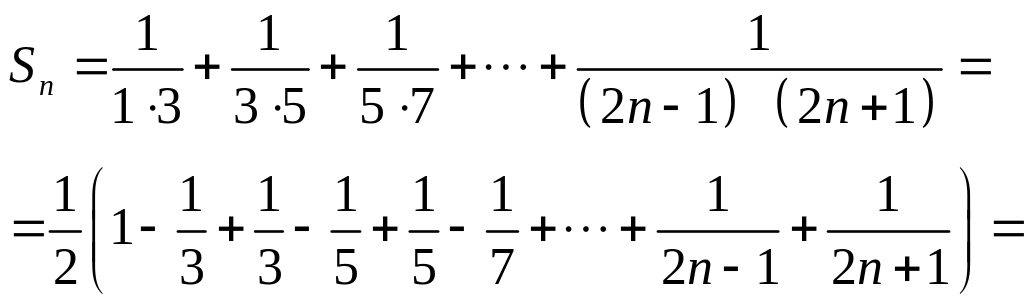
Обчислимо: . Це означає, що ряд збігається і має суму .

2. Необхідна ознака збіжності та достатня ознака розбіжності ряду

Теорема 1

(необхідна ознака розбіжності ряду)

Якщо ряд (1.1) збігається, то (2.1)

Виконання умови (2.1) не гарантує збіжності ряду, а лише інформує про її можливість. Існують ряди, для яких умова (2.1) виконується, але вони являються розбіжними.

Прикладом може бути так званий узагальнений гармонічний ряд . . Для .

Проте далі буде показано, що цей ряд збігається при і розбігається при . (див. приклад 11).

Теорема 2

(достатня ознака розбіжності ряду)

Якщо , то ряд (1.1) розбігається.

Приклад 4

Дослідити збіжність ряду .

Розв’язання

Обчислимо границю . Отже, заданий ряд за теоремою 2 розбіжний.

3. Ряди з додатними членами