План розв’язування задачі
1. Виділити тверде тіло, рівновагу якого потрібно розглянути для визначення невідомих величин та показати на рисунку активні сили.
2. Вибрати
систему декартових координат
.
3. Звільнити тіло від в’язей, їх дію замінити відповідними реакціями.
4. Розглянути рівновагу даного твердого тіла, яке перебуває під дією активних сил та реакцій в’язей. Для цього записати рівняння рівноваги.
5. Розв’язати рівняння рівноваги та визначити невідомі величини.
6. Виконати перевірку правильності визначення реакцій.
Розв’язування
1. Ломаний
стержень
перебуває у рівновазі під дією пари сил
з моментом
кНм,
зосереджених сил
кН та Q=10кН,
прикладених у точках К
та N.
2.
Вибираємо систему координат
.
3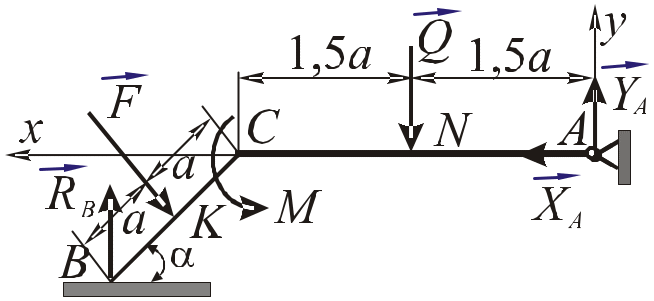
.
Звільняємо тіло від в’язей, а їх діє
замінюємо силами реакцій. Реакція
площини направлена вертикально, тобто
перпендикулярно до площини. Реакцію
шарнірно нерухомої опори А
розділяємо на дві
складові:
(рис. 9).
Рис. 9
4. Складаємо рівняння рівноваги
;
,
;
,
;
.
5. Розв’язуємо рівняння рівноваги та визначаємо невідомі величини.
З
останнього рівняння визначаємо реaкцію
:
.
З першого
рівняння знаходимо
:
.
З другого
рівняння знаходимо
.
6. Для перевірки правильності визначення опорних реакцій записуємо рівняння моментів відносно точки В:
.
Реакції визначені вірно.
Задача 2. Рівновага системи двох тіл (складної конструкції) Теоретична довідка
Система тіл – це сукупність твердих тіл які вільно спираються одне на одне чи з'єднані між собою в'язями.
Під дією довільної плоскої системи сил перебуває у рівновазі як система тіл, так і кожне тіло системи зокрема, причому всі сили, прикладені до нього, зрівноважені. Отже, для плоскої системи сил, що діє на складну конструкцію та на кожне тіло зокрема, можна скласти по три рівняння рівноваги.
Розв'язуючи задачі на рівновагу системи тіл, застосовують метод розчленування системи, відповідно до якого розглядають рівновагу кожного тіла системи окремо.
Розглядаючи рівновагу всієї системи, реакції в’язей між її тілами не беруть до уваги, оскільки стосовно всієї системи ці реакції є внутрішніми взаємно зрівноваженими силами.
Приклад 2.1. Визначити реакції в точках A, B, C тришарнірної рами, на яку діє сила F=10 кН. Розміри рами показані на рис. 10.
Р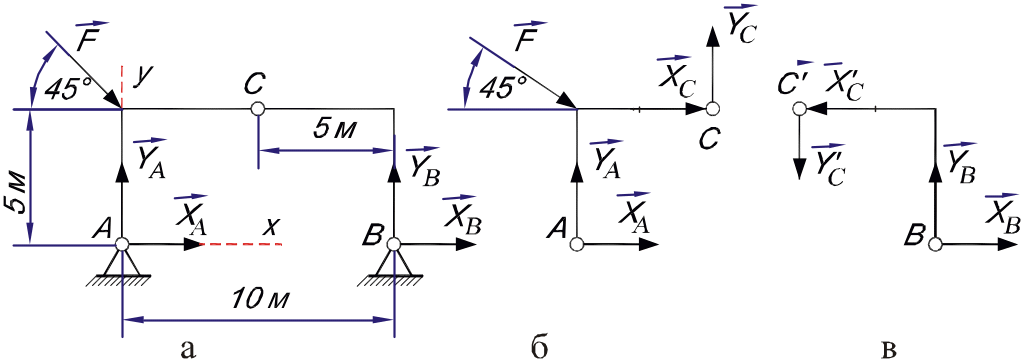
ис.
10
План розв’язування задачі
1. Розглянути рівновагу всієї системи та показати на рисунку активні сили.
2. Вибрати
декартову систему координат
.
3. Звільнити систему тіл від в’язей, а їх дію замінити відповідними реакціями в’язей.
4. Розглянути рівновагу системи твердих тіл, яка перебуває під дією активних сил та реакцій в’язей. Для цього записати рівняння рівноваги.
5. Розв’язати рівняння рівноваги та визначити деякі невідомі величини.
6. Розглянути рівновагу окремих тіл, які складають систему. З рівнянь рівноваги цих тіл визначають решту невідомих величин та реакцію в’язі між тілами системи.
7. Виконати перевірку правильності отриманих результатів.
Розв’язування
1. Розглядаємо рівновагу всієї конструкції.
2. Вибираємо осі
координат
так, як показано на рис. 10,
а.
3.
Звільняємо систему тіл від в'язей та
замінюємо їх дію реакцій
(рис. 10, а). Конструкція перебуває під
дією плоскої довільної системи сил.
4. Складаємо рівняння рівноваги для конструкції загалом:
;
;
;
;
;
.
Ці три рівняння містять чотири невідомі величини . Тому для повного розв'язання задачі використаємо метод розчленування конструкції на ліву (рис. 10, а) та праву (рис. 10,б) частини.
5.
Розглянемо рівновагу окремих частин
конструкції та визначимо реакції
і сили взаємодії в шарнірі
:
а) частина
(рис. 10, а)
;
;
;
;
;
;
б) частина
(рис. 10, б)
;
;
;
;
;
,
де
- сили взаємодії частин
і
у шарнірі
.
Оскільки ці сили зрівноважені, то за
модулями вони є однаковими
,
а за нпрямками – протилежнами.
Таким
чином, записані дві системи рівнянь
дозволяють визначити реакції
та сили взаємодії в шарнірі
-
.
Запишемо
системи рівнянь з урахуванням числового
значення заданої сили
.
Для частини :
;
;
.
Для частини :
;
;
.
З цих шести рівнянь визначаємо всі шість невідомих реакцій. Отримані числові значення:
- сили взаємодії у шарнірі
,
;
- реакції в опорі
,
;
- реакції в опорі
,
;
Знак «-» вказує на те, що дійсні напрямки сил є протилежними до тих, які вказані на рис. 10.
6. Перевіримо правильність визначення опорних реакцій . Для цього використаємо рівняння рівноваги всієї конструкції, одержані в п. 4. Після підстановки числових даних маємо
;
;
.
Реакції визначені вірно.