Задача 11

1. Границя суми кінцевого числа функцій дорівнює сумі границь цих функцій, тобто

.

2. Границя добутку кінцевого числа функцій дорівнює добутку границь цих функцій, тобто

.

3. Числовий сталий множник можна виносити з під знака границі, тобто

.

4. Границя від функції, що піднесено до кінцевого степеню, дорівнює границі цієї функції, піднесеній до того ж самого степеню:

.

5. Границя частки двох функцій дорівнює частці границь цих функцій, якщо границя знаменника не дорівнює нулю, тобто

, .

6. Функція є нескінченно малою величиною при , якщо

.

7. Функція є нескінченно великою величиною при , якщо

.

8. Величина обернена до нескінченно малої величини при , є нескінченно великою величиною при , тобто

.

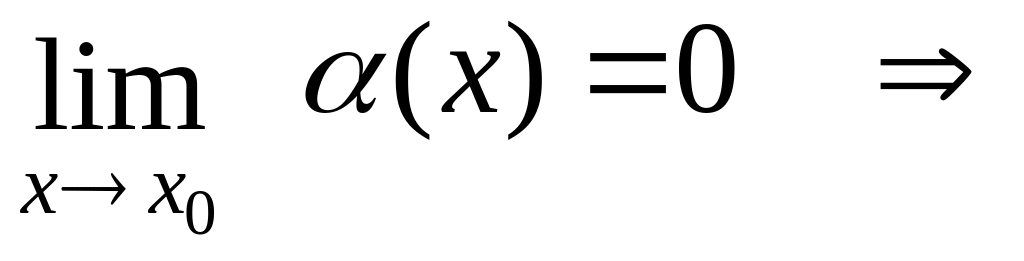
9. Величина обернена до нескінченно великої величини при , є нескінченно малою величиною при , тобто

.

10. Якщо при обчисленні границі отримано вирази вигляду або і , де 1 є границею деякої функції, то вони є невизначеностями. Щоб обчислити таку границю, необхідно виконати тотожні перетворення функції під знаком границі, які залежать від виду невизначеності і самої функції.

Задача 12

1. Многочленом n - го степеню відносно змінної х називається вираз:

,

де – числові коефіцієнти, .

2. Степінь многочлена визначається найбільшим степенем змінної х. Наприклад, многочлен має степінь ( ).

3. Коренем многочлена називається таке значення змінної х = х₀, при підстановці якого до многочлену, виконується умова:

.

4. Якщо х = х₀ є коренем многочлену , то цей многочлен можна представити у вигляді добутку різниці х – х₀ і многочлена (n–1) - го степеню відносно змінної х, тобто

.

Задача 13

1. Границя будь-якої елементарної функції при дорівнює значенню функції, що обчислено в точці , якщо ця точка належить області визначення функції: , де .

2. Границя функцій і при дорівнює 0, тобто

, .

3. Границя функції при дорівнює 1, тобто

.

4. Перша стандартна границя: границя функції при є невизначеністю вигляду , яка дорівнює 1, тобто

5. Перша стандартна границя для аргументу , що є нескінченно малою величиною при :

.

Задача 14

1. Число е – це ірраціональне число: .

2. Границя функції при дорівнює 1, тобто

.

3. Друга стандартна границя: границя функції при є невизначеністю вигляду , яка дорівнює числу е, тобто

.

4. Друга стандартна границя для аргументу , що є нескінченно великою величиною при :

.

5. Друга стандартна границя для аргументу , що є нескінченно малою величиною при :

.

Задача 15

1. Число А називається правосторонньою границею функції y = в точці x = а, якщо аргумент х прямує до точки x = а, але при цьому залишається більшим ніж а, тобто:

.

2. Число А називається лівосторонньою границею функції y = в точці x = а, якщо аргумент х прямує до точки x = а, але при цьому залишається меншим ніж а, тобто:

.

4. Функція y = є неперервною в точці x = а , якщо її границя дорівнює значенню функції в цій точці:

5. Якщо функція y = в точці x = а має границю, тобто

,

то ця границя дорівнює правосторонній і лівосторонній границі функції:

.

6. Умова неперервності функції y = в точці x = а: якщо лівостороння границя функції y = в точці x = а дорівнює її правосторонній границі і дорівнює значенню функції в цій точці, тобто:

,

то функція є неперервною в точці x = а.

7. Якщо в точці x = а з будь-яких причин не виконується умова неперервності функції, то ця точка називається точкою розриву функції. Функція, що має точки розриву, називається розривною. Розрізняють точки розриву І роду і ІІ роду.

8. Схема дослідження функції y = на неперервність в точці x = а:

– знайти область визначення функції;

• з‘ясувати, чи належить точка x = а області визначення функції;

• знайти правосторонню границю функції y = в точці x = а, тобто ;

• знайти лівосторонню границю функції y = в точці x = а, тобто

;

• обчислити, якщо можливо, значення функції y = в точці x = а.

9. В таблиці 1 наведено ознаки неперервності функції і наявності точок розриву.

Таблиця 1

Ознаки	Належність точки x = а до області визначення функції	Існування односторонніх границь функції в точці x = а	Рівність між значенням функції в точці x = а і односторонніми границями
Функція неперервна в точці x = а	Функція визначена в точці :	Існує правостороння границя ; Існує лівостороння границя ; А, В – скінчені числа
Функція має в точці x = а розрив І роду	Функція визначена в точці :	Існує правостороння границя ; Існує лівостороння границя ; А, В – скінчені числа;	=А , або = , або
	Функція не визначена в точці :		, не існує
Функція має в точці x= а розрив І роду, що усувається	Функція визначена, в точці :	Існує правостороння границя ; Існує лівостороння границя ; А, В – скінчені числа;
	Функція не визначена в точці :		, не існує
Функція має в точці x = а розрив ІІ роду	Функція може бути визначена, а може бути не визначена в точці : , або	Хоча б одна з односторонніх границь дорівнює нескінченості, або не існує: , або , або не існують	Значення функції у= може існувати, а може і не існувати.

10. Рівняння – це рівняння прямої на площині, де – числові коефіцієнти. Для того, щоб побудувати пряму, потрібно:

а) для двох довільних значень аргументу обчислити відповідні значення функції ;

б) на координатній площині відмітити точки ;

в) провести пряму лінію через точки .

11. Рівняння – це рівняння параболи на площині, де – числові коефіцієнти. Для того, щоб побудувати параболу, потрібно:

а) обчислити координати вершини параболи – точки , де

б) знайти координати точок перетину параболи з віссю : точок і , де .

У разі, коли , парабола перетинає вісь ОХ в точці , а коли – парабола не перетинає вісь ОХ;

в) на координатній площині відмітити точки і точку – точку перетину з віссю OY.

г) провести плавну лінію через точки , В, і С, таким чином, щоб пряма була її віссю симетрії.

12. Рівняння – це рівняння логарифмічної функції, де – числовий коефіцієнт. Для того, щоб побудувати графік функції, потрібно:

а) провести пунктирною лінією пряму , яка є асимптотою графіка функції;

б) на координатній площині відмітити точку – точку перетину графіка функції з віссю OХ;

в) для декількох значень аргументу

обчислити відповідні значення функції ;

г) на координатній площині відмітити точки , і точку В;

д) провести плавну лінію, яка проходить через точки , B, яка при справа наближається до прямої .