Задача 6

1. Рівняння площини, що проходить через точку перпендикулярно вектору : .

2. Рівняння площини, що проходить через три точки , і можна отримати з умови:

3. Загальне рівняння площини:

де – вектор нормалі, що є перпендикулярним площині.

4. Кут між площинами, що задаються рівняннями

і ,

дорівнює куту між векторами нормалі площин і . Косинус кута дорівнює: .

Задача 7

1. Рівняння прямої у просторі, що проходить через дві точки і :

2. Канонічні рівняння прямої у просторі, що проходить через точку паралельно вектору :

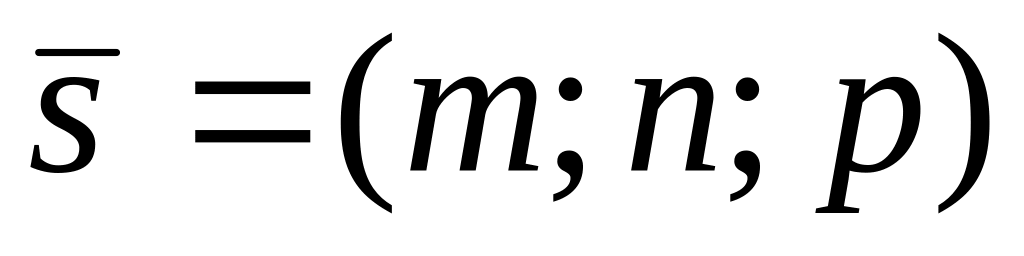Вектор називається напрямним вектором прямої у просторі.

3. Кут між прямими у просторі, що задаються рівняннями

і ,

дорівнює куту між напрямними векторами цих прямих, а саме і . Косинус кута дорівнює:

.

Задача 8

1. Рівняння прямої у просторі, що проходить через точку перпендикулярно площині :

2. Параметричні рівняння прямої у просторі можна отримати з канонічних рівнянь Для цього кожне відношення канонічних рівнянь прирівнюють параметру :

Рівняння, що отримані, розв‘язують відносно змінних . В результаті отримають параметричні рівняння прямої у просторі: .

3. Щоб знайти точку перетину прямої, що має параметричні рівняння , і площини, що має загальне рівняння необхідно замість змінних в рівняння площини підставити параметричні рівняння прямої. В результаті буде отримане рівняння відносно однієї змінної : .

Розв‘язком цього рівняння є значення параметра , яке треба підставити в параметричні рівняння прямої. Таким чином будуть отримані координати точки перетину прямої і площини:

Задача 9

1. Рівняння прямої на площині, що проходить через дві точки і :

2. Рівняння прямої на площині у вигляді рівняння з кутовим коефіцієнтом:

,

де – кутовий коефіцієнт прямої, – кут між прямою і додатним напрямком вісі ОХ , b – координата перетину прямої з віссю ОY.

3. Координати точки , що розподіляє відрізок навпіл ( ):

4. Рівняння прямої на площині, що проходить через точку , з відомим кутовим коефіцієнтом : .

5. Ознака перпендикулярності прямих і на площині, що задаються рівняннями і :

.

6. Відстань між точками і на площині:

.

Задача 10

1. Гіперболою називається множина точок на площині, для яких модуль різниці відстаней до двох фіксованих точок , які називають фокусами, є сталою величиною 2а, що менша за відстань між фокусами.

2. На рис.1 зображено гіперболу, де позначено М - точку гіперболи; і - фокуси гіперболи; та – фокальні радіуси; – відстань між фокусами; – модуль різниці відстаней від точки гіперболи до фокусів ; а – дійсна піввісь гіперболи; і - дійсні вершини гіперболи; – відстань від точки М до директриси; – ексцентриситет гіперболи; – уявна піввісь гіперболи.

3. Канонічне рівняння гіперболи, що зображено на рис.1:

.

Гіпербола має дві асимптоти . Це прямі

4. Гіпербола є множиною точок площини, відношення відстаней від яких до фіксованої точки (фокуса) і деякої прямої (директриси) є величина стала, більша за одиницю. Це відношення є ексцентриситетом гіперболи.

Прямі називаються директрисами гіперболи..

5.

6. Еліпсом називається множина точок площини, для яких сума відстаней до двох фіксованих точок , які називають фокусами, є сталою величиною 2а, більшою за відстань між фокусами.

7. На рис.3 зображено еліпс, де позначено М - точку еліпса; і - фокуси еліпса; та – фокальні радіуси; – відстань між фокусами; – сума відстаней від точки еліпса до фокусів ; , , , - вершини еліпса; – відстань від точки М до директриси; – ексцентриситет; , – піввісі еліпса.

Рис.3

8. Канонічне рівняння еліпса, що зображено на рис.3:

.

В цьому випадку еліпс витягнуто вздовж вісі ОХ. Фокуси еліпса в цьому разі мають координати , .

9. У разі, коли , еліпс витягнуто вздовж вісі ОY. В цьому випадку . В цьому разі фокуси еліпса лежать на вісі ОY і мають координати:

, .

10. Відношення називається ексцентриситетом еліпса.

11. Прямі називаються директрисами еліпса.

12. Справедливо наступна властивість директрис: відношення відстаней від фокусу і директриси для точок еліпса є величина стала, яка дорівнює ексцентриситету.

13. Коло – це геометричне місце точок на площині, відстань від яких до деякої фіксованої точки, що називається центом кола, є величиною сталою. Яка називається радіусом кола. Канонічне рівняння кола с центром в точці , радіус якої дорівнює , має вигляд:

.

14. Канонічне рівняння кола с центром в точці - початку координат, радіус якої дорівнює , має вигляд:

.

15. Для того, щоб привести до канонічного вигляду рівняння потрібно розділити обидві його частини на число, що стоїть в правій частині рівняння. В результаті буде отримано рівняння:

.

В залежності від знаків чисел і може бути один з випадків:

а) – отримано рівняння еліпса;

б) – отримано рівняння кола;

в) або – отримано рівняння гіперболи;

г) – лінія з таким рівнянням не існує.