2.2 Розтягання (стикання) призматичних стрижнів. Визначення напружень. Розрахунок на міцність

У даному курсі розглянуті стрижні постійного поперечного перерізу з прямолінійною віссю, тобто призматичні стрижні.

Під розтяганням (стиканням) розуміють такий вигляд деформації стрижня, при якому в його поперечному перерізі виникає лише один внутрішній силовий чинник – подовжня сила N_z. Оскільки подовжня сила чисельно дорівнює сумі проекцій, прикладених до однієї з відсічених частин зовнішніх сил на вісь стрижня (для прямолінійного стрижня вона збігається в кожному перерізі з віссю Oz), то розтягання (стикання ) має місце, якщо всі зовнішні сили, що діють з одного боку від даного поперечного перерізу, зводяться до рівнодійної, направленої уподовж осі стрижня (рис. 2.1). Одна і та ж подовжня сила N_z при дії на різні частини стрижня (ліву або праву) має протилежні напрямки. Знак N_z залежить від характеру деформації, що викликається нею. Подовжня сила вважається додатною, якщо викликає розтягання елемента (рис. 2.2, а), і вона від`ємна, якщо викликає стикання (рис. 2.2, б).

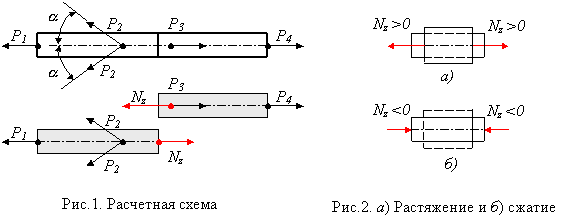
Рисунок 2.1 – Розрахункова схема

а – розтягання, б – стикання

Рисунок 2.2 – Елемент стрижня

Для того щоб сформулювати передумови теорії розтягання (стикання) призматичного стрижня, звернемося до експерименту. Уявимо собі стрижень, виготовлений з якого-небудь податливого матеріалу (наприклад, гуми), на бічну поверхню якого нанесена система подовжніх і поперечних рисок (рис. 2.3, а). Ця ортогональна система рисок залишається такою і після прикладання розтягуючого навантаження (рис. 2.3, б).

Рисунок 2.3 – Модель розтягнутого стрижня

Оскільки поперечні риски є слідами поперечних перерізів на поверхні стрижня і залишаються прямими і перпендикулярними до осі стрижня, то це свідчить про виконання гіпотези плоских перерізів (Бернуллі). З врахуванням гіпотези про відсутність поперечної взаємодії подовжніх волокон доходимо до висновку, що деформація розтягування стрижня зводиться до одноосного розтягування його подовжніх волокон, і в поперечному перерізі стрижня виникають лише нормальні напруження  (рис. 2.4). Ортогональність подовжніх і поперечних рисок свідчить також про відсутність зрушень, а отже, і пов'язаних з ними дотичних напружень  в поперечних і подовжніх перерізах стрижня.

Рисунок 2.4 – Зв'язок напружень та зусиль

Тоді подовжня сила N_z дорівнює сумі проекції внутрішніх сил, що діють у даному поперечному перерізі площею F (рис. 2.4) очевидно буде дорівнювати

де  – нормальне напруження або інтенсивність внутрішніх сил, що виникають в тілі, що деформується, під впливом зовнішніх дій.

Це співвідношення є рівнянням рівноваги статики, що зв'язує подовжню силу N_z, і нормальне напруження , яке в загальному випадку є функцією координат х і у і тому не може бути знайдено з одного лише рівняння статики. Таким чином, завдання визначення напружень навіть в найпростішому випадку деформації стрижня (розтягуванні або стикуванні) являється статично не визначуваним.

Необхідне для вирішення цього завдання додаткове рівняння витікає з гіпотези плоских перерізів. Оскільки поперечні перерізи стрижня, залишаючись плоскими і перпендикулярними до осі стрижня, у процесі деформації лише поступально переміщаються уздовж осі стрижня (що приводить до однакового подовження всіх повздовжніх волокон), то приходимо до рівняння  =const, з якого, зважаючи на однозначність зв'язку  і  (для лінійно-пружнього матеріалу це закон Гуку: =Е), витікає

 = const.

Вирішуючи спільно рівняння, отримаємо, що

N_z=F

або

 = N_z / F.

Таким чином, при розтяганні (стиканні) призматичного стрижня нормальні напруження рівномірно розподілені за поперечним перерізом, а дотичні напруження в перерізах відсутні, що є наслідком гіпотези плоских перерізів. Указане, є фундаментальним результатом, справедливим тільки для призматичного стрижня, однак в інженерній практиці його використовують і для наближеної оцінки нормальних напружень в стрижнях змінного перерізу. При цьому, щоб нев’язка формули була невеликою, необхідно, щоб площа поперечного перерізу стрижня змінювалася достатньо повільно уздовж його осі.

Умова міцності при розтяганні (стиканні) призматичного стрижня з пластичного матеріалу (тобто матеріалу, що однаково працює на розтягання і стикання ) набуде виду:

, (2.1)

де [] – допустиме напруження. Напруження  в умові (2.1) підставляється за модулем, оскільки знак  у цьому випадку ролі не грає.

У практиці інженерних розрахунків, виходячи з умови міцності, розв’язуються три основні задачі механіки матеріалів конструкцій. У застосуванні до випадку розтягання (стикання) призматичного стрижня ці задачі формулюються таким чином.

Перевірка міцності (перевірочний розрахунок). Цей розрахунок проводиться, якщо навантаження (у нашому випадку її представляє N_z), переріз стрижня F і характеристики його матеріалу [] задані.

Необхідно переконатися, що виконується умова міцності:

Перевірочний розрахунок полягає в тому, що визначається фактичний коефіцієнт запасу міцності n і порівнюється з нормативним коефіцієнтом запасу [n]:

,

де – граничне (або небезпечне) напруження, тобто напруження, що викликає відмову елемента конструкції (для стрижня з пластичного матеріалу це – границя текучості _т або умовна границя текучості _0,2).

Підбір перерізу (проектний розрахунок). У цьому розрахунку за заданим навантаженням (N_z) визначаються розміри поперечного перерізу стрижня (F) із заданого матеріалу ([] дано). Мінімального значення F набудемо, якщо в умові міцності (1) прийняти знак рівності:

[F] = N_z / [].

Визначення навантаження, що допускається, тобто максимального значення навантаження, яке допускає даний елемент конструкції (F і [] дано) при виконанні умови міцності (2.1):

[N] = []F.