5.1.3 Плоский деформований стан

При плоскому деформованому стані всі деформації знаходяться в одній площині (рис. 5.3).

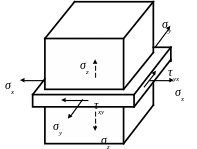
Рисунок 5.3 – Плоский деформований стан

Тоді узагальнений закон Гука запишеться так:

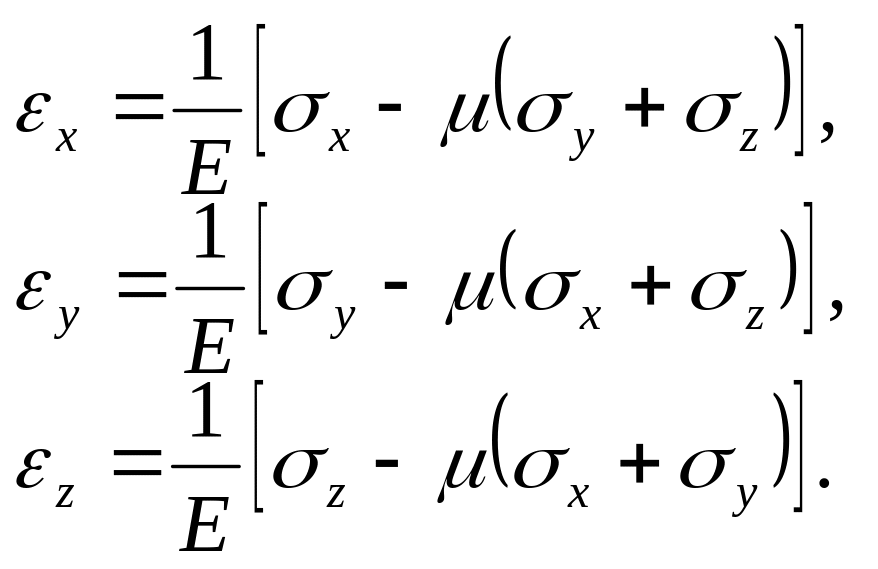
Звідси визначаємо і підставляємо в е_x і е_y: ,

(5.4)

Напруження через деформації рівні:

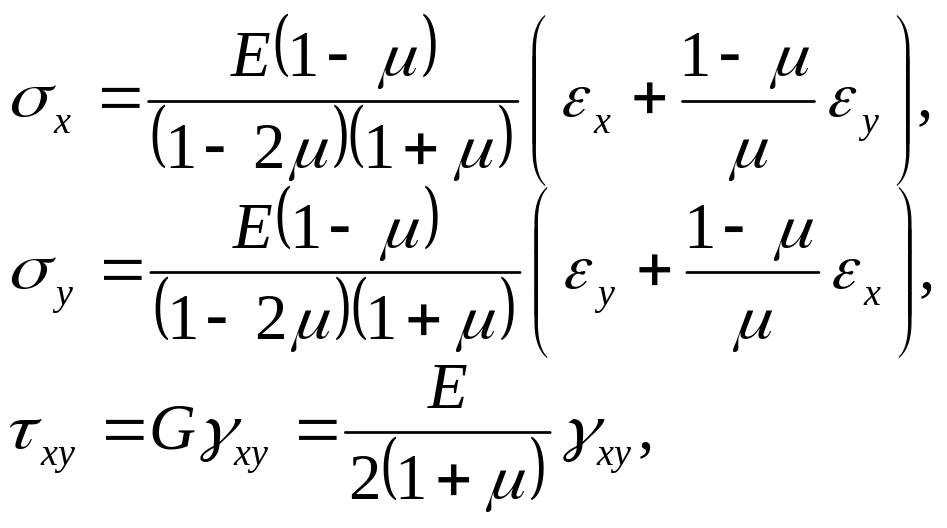
або в матричній формі:

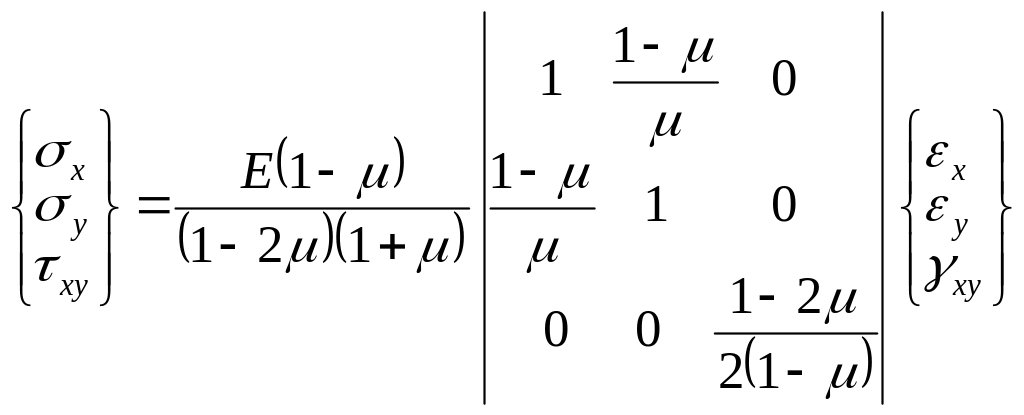. (5.5)

5.1.4 Зв'язок між деформаціями і переміщеннями

Розглянемо деформацію елемента з розмірами і (рис. 5.4).

Під дією сил елемент деформується (на рис. 5.4 показано пунктиром).

Визначимо відносні деформації і :

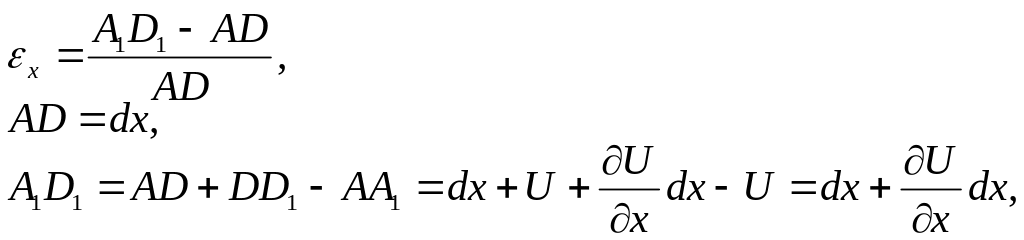
приблизно визначаємо проекції на вісь :

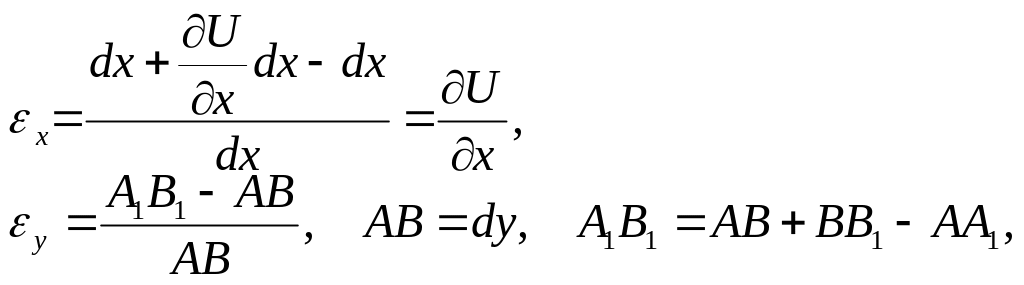
приблизно визначаємо проекції на вісь :

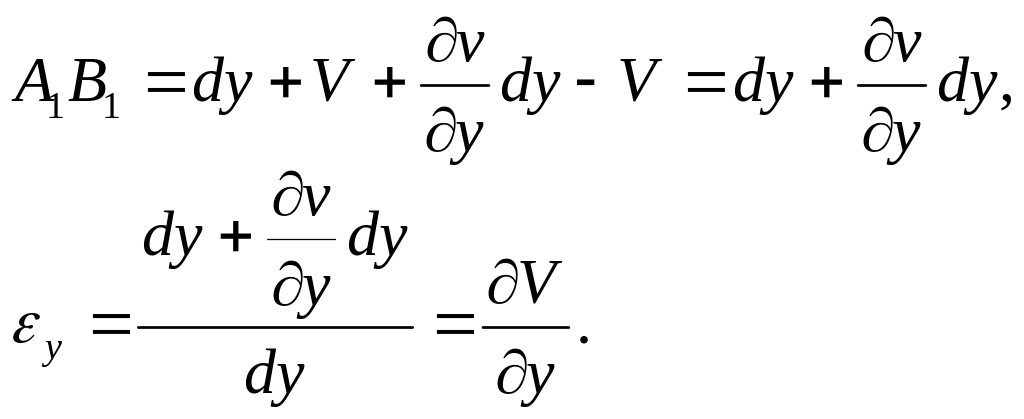
Рисунок 5.4 - Елемент АВСД до і після деформації

Відносним зсувом називають зменшення прямого кута .

Він дорівнює :

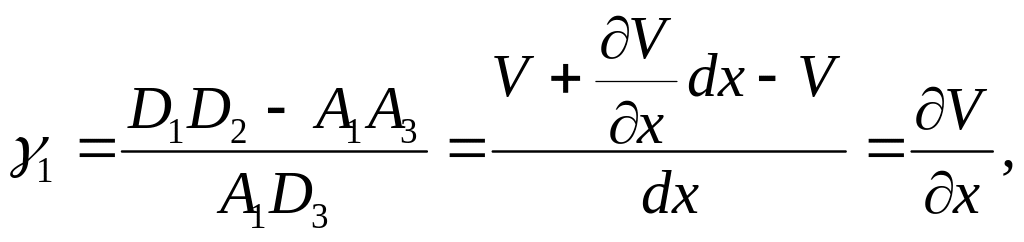
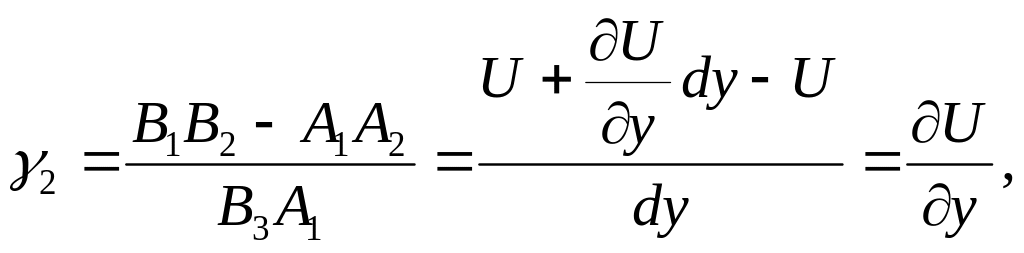
таким чином,

У матричній формі маємо відомі залежності Коші:

. (5.6)

5.1.5 Зв'язок між напруженнями і переміщеннями

Виразимо напруження через переміщення. Для цього у вирази (5.3) і (5.5) необхідно підставити залежність (5.6).

Для плоского напруженого стану:

, (5.7)

де - (5.8)

Для плоского деформованого стану:

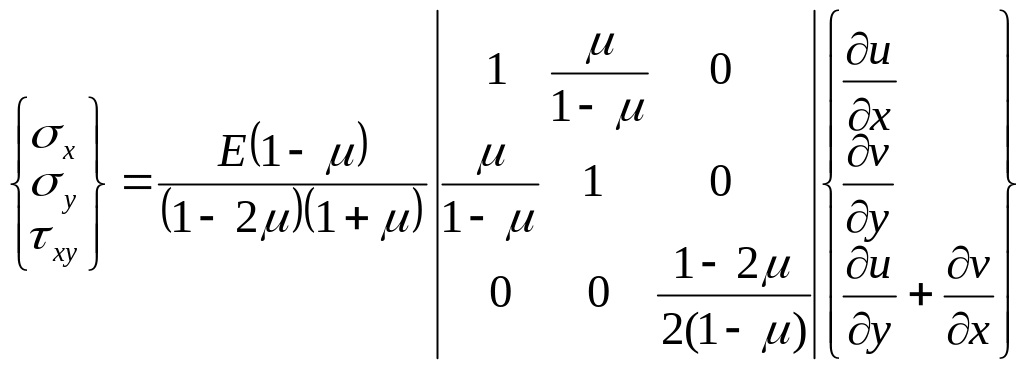, (5.9)

де

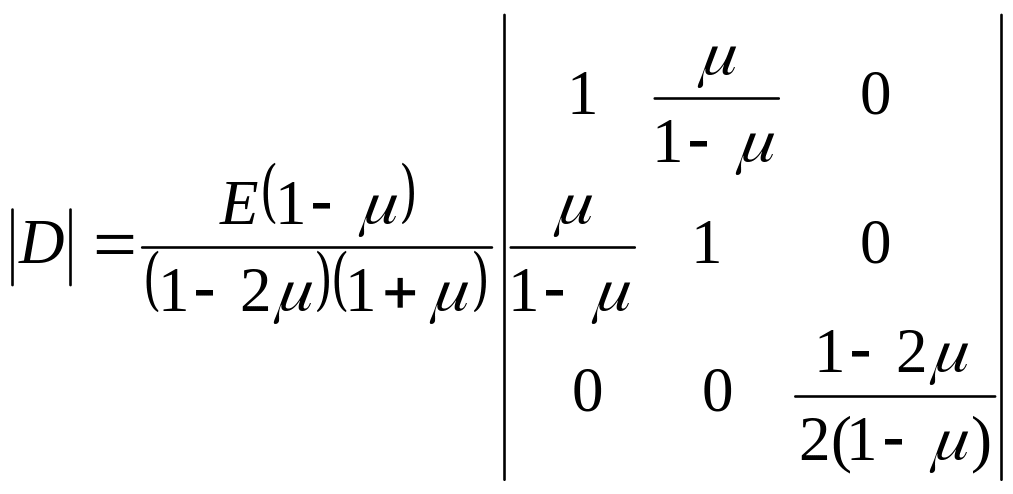(5.10)

5.2 Особливості осесимметричної задачі теорії пружності

Дослідження розподілу напружень в тілах обертання (вісесиметричних тілах) при вісесиметричному вантаженні викликає великий практичний інтерес. Ці задачі тривимірні, але з практичної точки зору вони аналогічні задачам про плоский напружений стан, так як унаслідок симетрії деформований, а отже, і напружений стан у будь-якому перерізі уздовз осі симетрії тіла повністю визначається двома компонентами переміщення.

У вісесимметричному випадку (рис 5.5) будь-яке радіальне переміщення викликає деформацію в окружному напрямку, і так як напруження в цьому напрямку не дорівнюють нулю, для розгляду має бути введена четверта компонента деформації у відповідному напрямку. У цьому полягає відмінність вісесимметричного випадку від плоскої задачі теорії пружності.

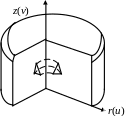
Рисунок 5.5 – Вісесимметричне тіло та торовидний кінцевий елемент

Вектор деформації тепер має вигляд:

(5.11)

як і для плоского задачі.

Визначимо відносну деформацію в окружному напрямку (рис 5.6):

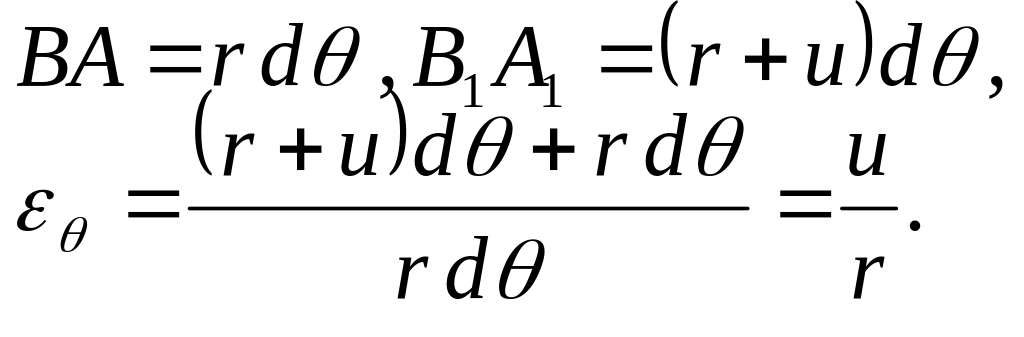
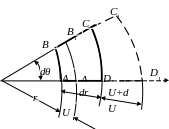
Рисунок 5.6 – Елемент вісесиметричного тіла до та після деформації

Таким чином, вектори напружень та деформацій в цьому випадку мають вигляд:

(5.12)

(5.13)

Остаточно

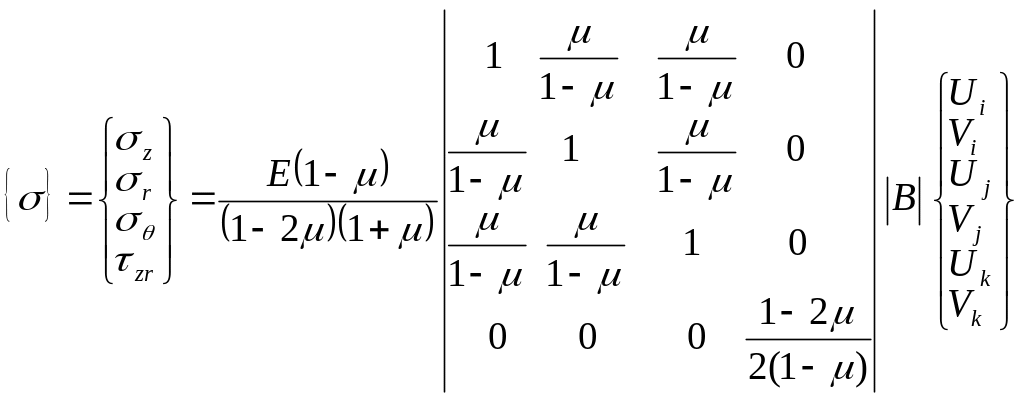. (5.14)

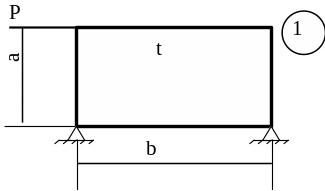
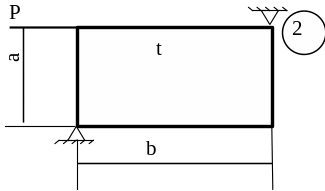
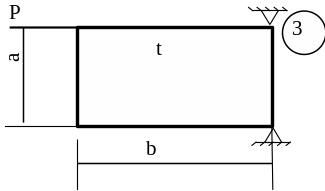
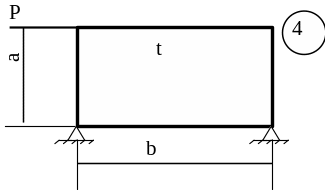
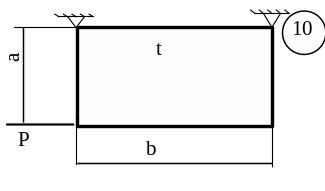
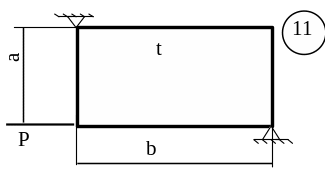
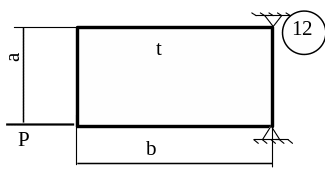
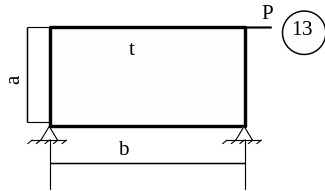
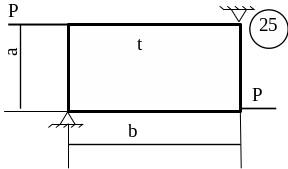
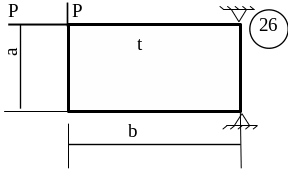
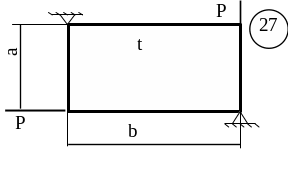
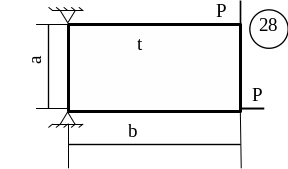
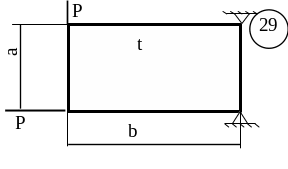
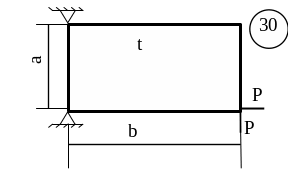
5.3 Лабораторна робота 9

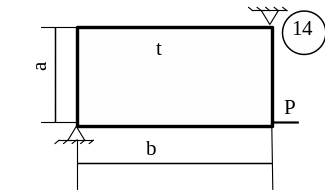
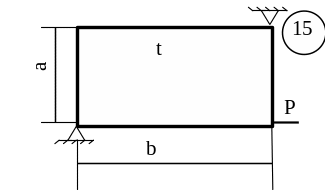
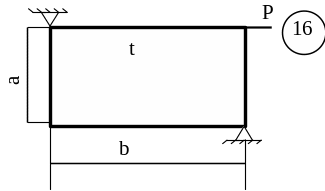
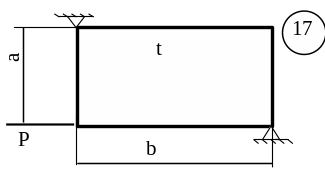
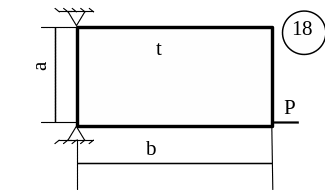
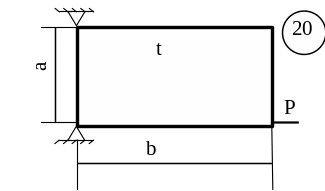
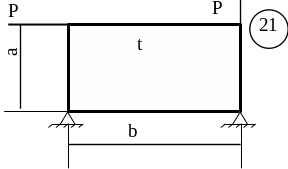
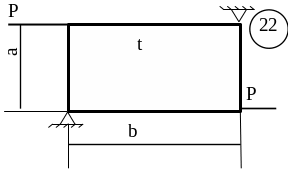
Для заданої пластини товщиною t і розмірами в плані ab необхідно визначити внутрішні напруження, якщо МПа, .

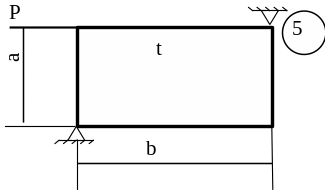
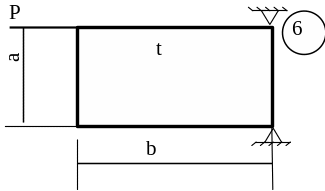
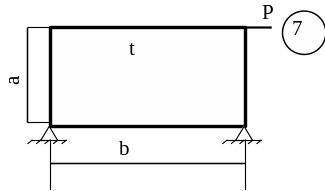
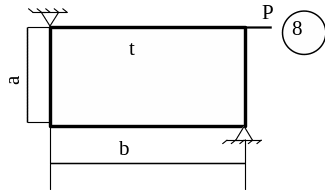
Схему для вирішення завдання узяти з рисунка 5.7, дані з таблиць 5.1. та 5.2.

Таблиця 5.1

Величина, м	Значення величини відповідно до першої цифри номера варіанта
	0	1	2	3	4	5	6	7	8	9
a	0,8	0,5	1,0	1,2	0,5	0,4	0,2	0,5	0,8	0,6
b	0,2	0,2	0,4	0,6	0,6	0,8	0,4	0,6	0,6	0,4

Таблиця 5.2

Величина	Значення величини відповідно до другої цифри номера варіанта
	0	1	2	3	4	5	6	7	8	9
P, кН	200	260	240	220	280	300	250	280	260	300

Рисунок 5.7

Рисунок 5.7, аркуш 2

Рисунок 5.7, аркуш 3

Указівки до виконання лабораторної роботи 9

1. Поділяємо пластину на кінцеві елементи. Нумеруємо отримані елементи і вузли (зручно брати як кінцеві елементи ділянки стрижня).

2. Обчислюємо матрицю пружності кожного з кінцевих елементів:

.

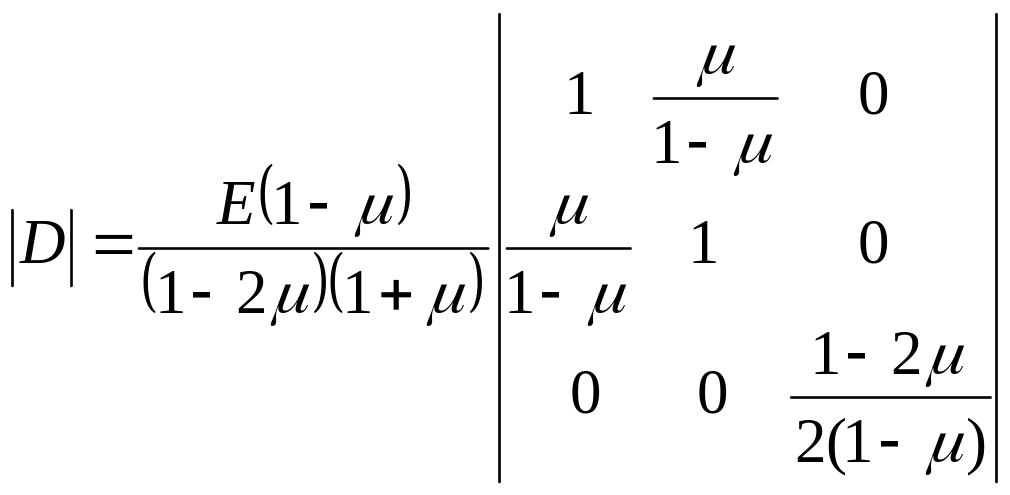3. Обчислюємо статичну матрицю кожного з елементів:

,

де  – площа кінцевого елемента

інші коефіцієнти одержуються круговою перестановкою індексів.

4. Обчислюємо матрицю жорсткості кожного з елементів:

,

де t – товщина пластини.

5. Формуємо матрицю жорсткості конструкції як ансамбль матриць жорсткості кінцевих елементів, з яких складається конструкція. Її порядок дорівнює кількості вузлів помноженому на два.

6 Записуємо систему рівнянь виду

де К – матриця жорсткості конструкції в цілому;

– вектор кутів повороту всіх вузлів;

– вектор вузлових навантажень.

7 З розв’язання системи рівнянь, з урахуванням граничних умов, знаходяться переміщення вузлів.

8 Визначаються величини внутрішніх напружень:

Приклад виконання лабораторної роботи 9

Для пластини, показаної на рисунку 5.8, необхідно визначити нормальні напруження, що виникають під дією зовнішніх факторів.

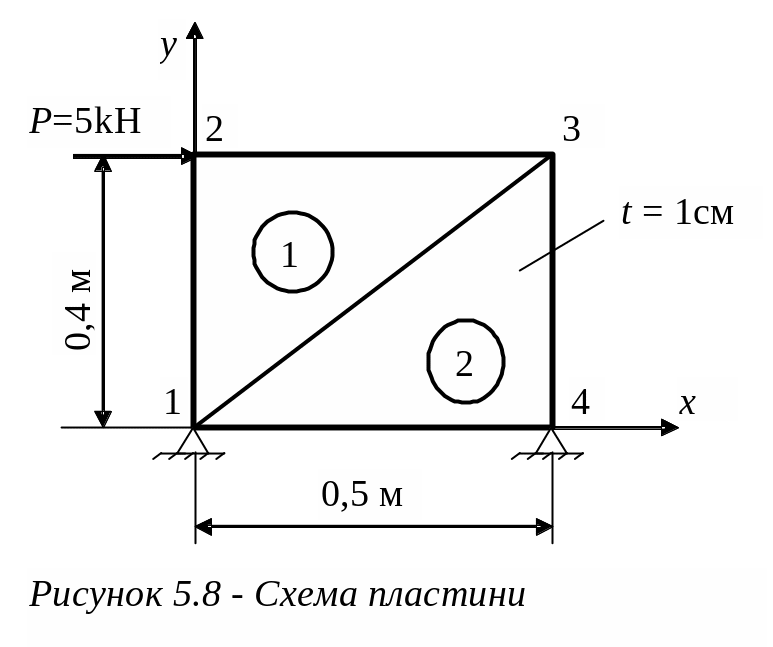
Розв’язок. Поділяємо пластину на елементи. Для ілюстрації МКЕ поділяємо всього на 2 елементи (природно, такий поділ дуже приблизний і не забезпечує точності розрахунку). Нумеруємо вузли і елементи.

Переходимо до обчислення матриць жорсткості елементів.

1-й елемент: його зв'язки 1-3-2 (починаємо з меншого номера і називаємо вузли, обходячи їх проти ходу годинникової стрілки).

Тобто i-й вузол –1, j-й – 3, k-й –2.

Обчислюємо коефіцієнти а,b і c :

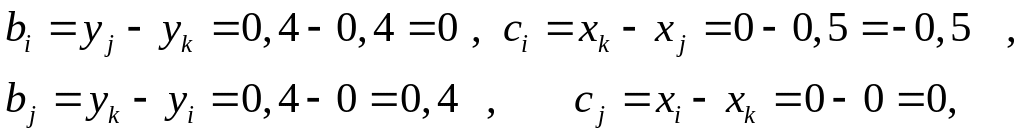
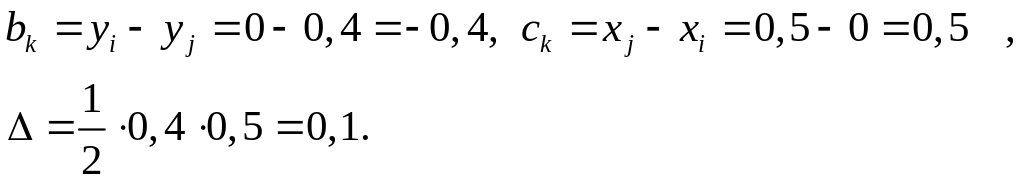
Матриця дорівнює:

Матриця жорсткості першого елемента:

2-й елемент: його зв'язки 1-4-3 . Аналогічно визначаємо:

.

Формуємо матрицю жорсткості конструкції. Оскільки пластина має чотири вузли, а кожен вузол має два степені вільності, то розмір матриці жорсткості конструкції – 8х8. При занесенні коефіцієнтів до матриці жорсткості конструкції слід уважно стежити, які вузли включають елементи і яка їх послідовність.

До правої частини заносимо навантаження, прикладені у вузлах. Оскільки навантаження прикладене тільки в другому вузлі в горизонтальному напрямку, то заносимо до третього рядка навантаження (переведене в меганьютони (MH)). В останніх рядках ставимо нулі.

481 1077	0 0	-481	385	0 0	-385 -577	1077	577
0 0	1082 308	577	-1682	-577 -385	0 0	385	-308
-481	577	1558	-962	-1077	385	0	0
385	-1682	-962	1990	577	-308	0	0
0 0	-577 -385	-1077	577	1077 481	0 0	-481	385
-385 -577	0 0	385	-308	0 0	308 1682	577	-1682
-1077	385	0	0	-481	577	1558	-962
577	-308	0	0	385	-1682	-962	1990

Ураховуємо граничні умови:

Після їх урахування отримаємо:

Вирішуючи систему рівнянь, знайдемо:

, , , .

Визначаємо напруження в елементах.

1-й елемент:

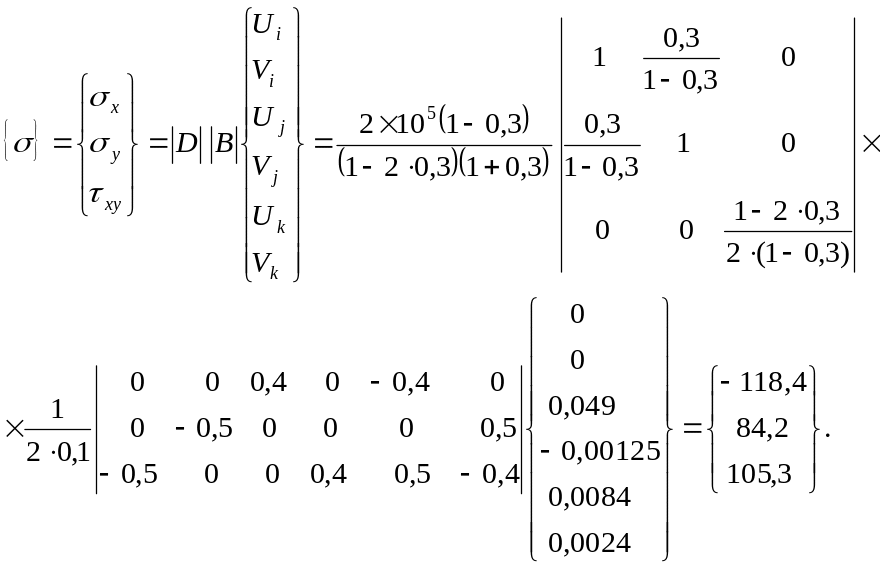
2-й елемент:
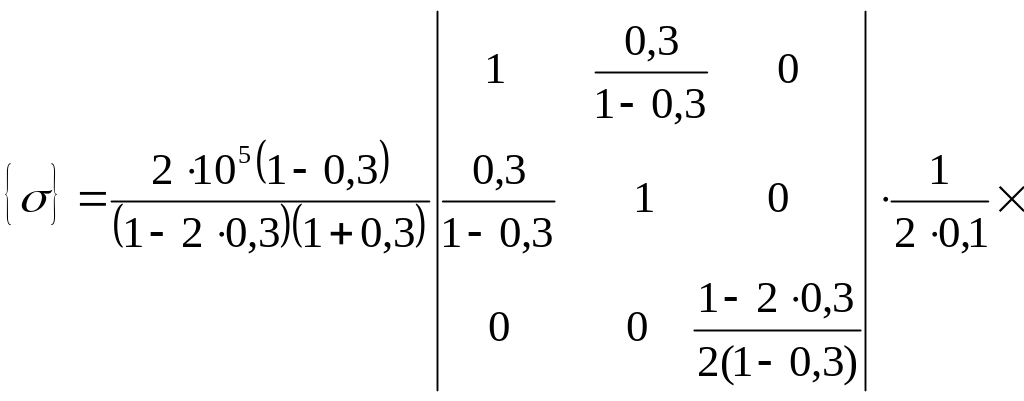