
Задание №1.
В коробке смешаны электролампы одинакового размера и формы:
по 150 Вт – 5 + (К + М)(mod6) штук и по 100 Вт – 10 + (К + М)(mod6). Вынуты из коробки наугад три лампы. Найти вероятность того, что среди них:
а) только одна лампа по 150 Вт;
b) две лампы по 150 Вт;
с) не менее двух ламп по 150 Вт;
d) хотя бы одна лампа по 150 Вт;
е) все лампы одинаковой мощности.
Решение:
В коробке смешаны электролампы одинакового размера и формы:
по 150 Вт – 5 + (1 + 1)(mod6)= 7 штук
и
по 100 Вт – 10 + (1 + 1)(mod6)=12 штук.
Всего: 7+12=19 штук.
Пусть события:
А – среди трех наугад вынутых ламп будет только одна по 150 Вт,
В – будет две лампы по 150 Вт,
С – будет не менее двух ламп по 150 Вт, эти события независимы,
D- хотя бы одна лампа по 150 Вт, E- все лампы по 150 Вт, F- все лампы по 100 Вт, S – лампы одинаковой мощности.
Тогда:
а) только одна лампа по 150 Вт:
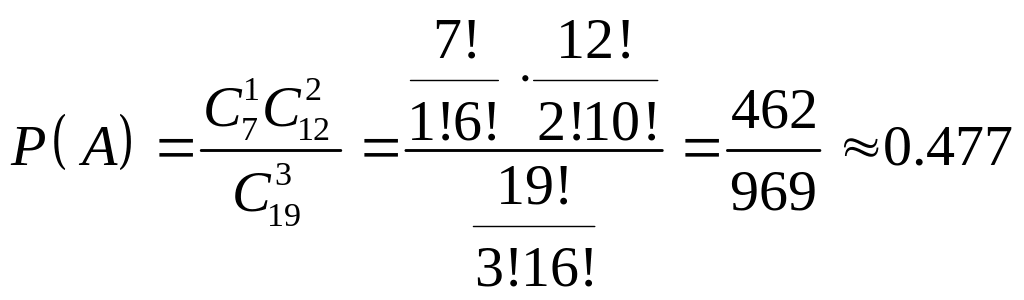 или
47,7%;
или
47,7%;
b) две лампы по 150 Вт:
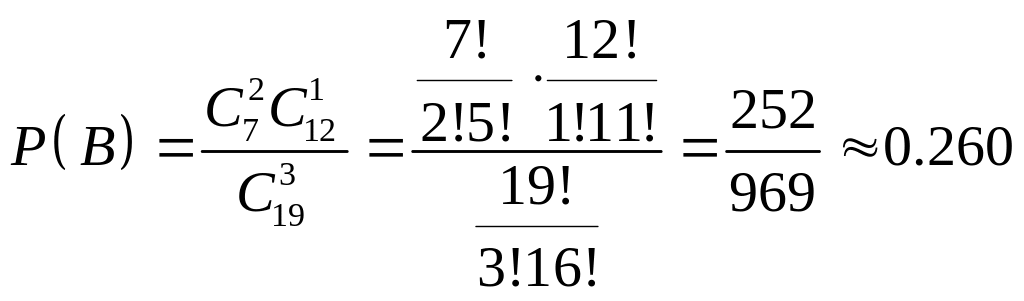 или
26%;
или
26%;
c) не менее двух ламп по 150:
Р(не менее двух ламп по 150 Вт)=( две лампы по 150 Вт или три лампы по 150 Вт)
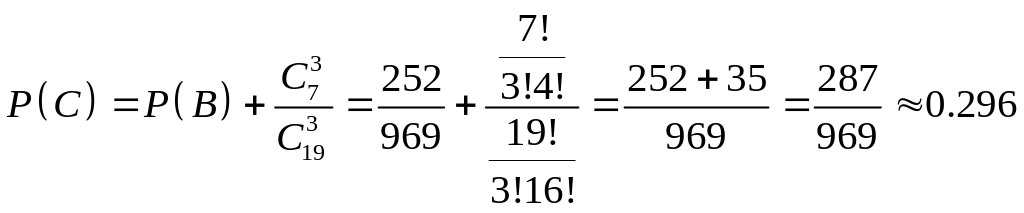 или
29,6%;
или
29,6%;
d) хотя бы одна лампа по 150:
Р( хотя бы одна лампа по 150 Вт)=1-(ни одной по 150 Вт)
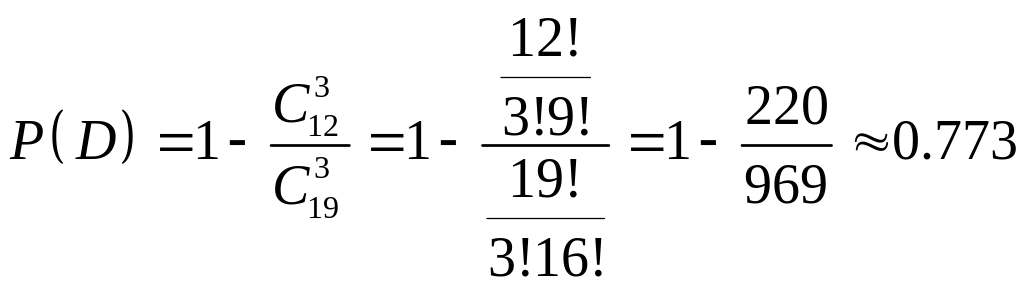 или
77,3%;
или
77,3%;
e) все лампы одинаковой мощности:
Р(лампы одинаковой мощности) =Р( все лампы по 150 Вт или все лампы по 100 Вт)
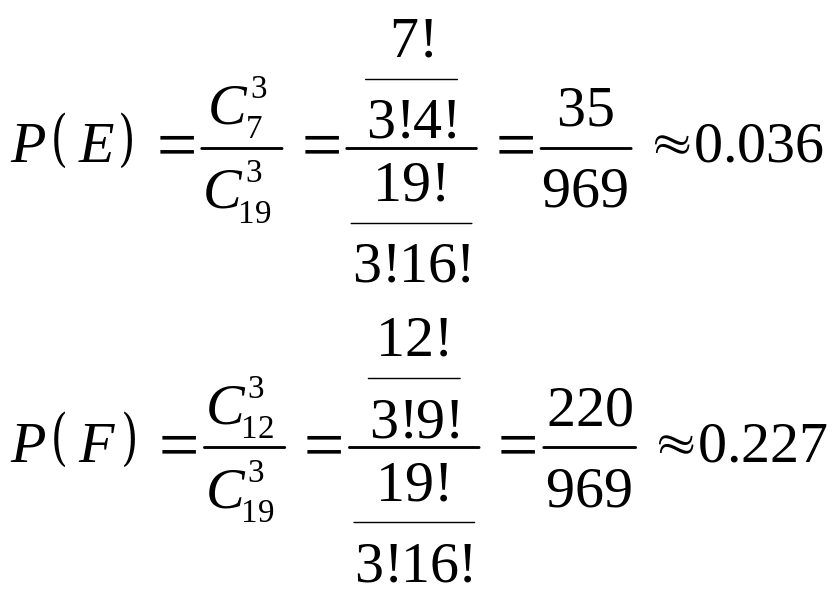
Тогда
![]() или
26,3%
или
26,3%
Ответ:
Вероятность того, что среди трёх наугад вынутых ламп:
а)
только одна лампа по 150 Вт: Р(А)![]() 47,7%
47,7%
b) две лампы по 150 Вт: Р(В) 26%
с) не менее двух ламп по 150: Р(С) Вт 29,6%
d) хотя бы одна лампа по 150: Р(D) Вт 77,3%
е) все лампы одинаковой мощности: Р(S) 26,3%
Задание №2.
По самолету производится три независимых выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,7. Для вывода самолета из строя достаточно трех попаданий. При двух попаданиях он выходит из строя с вероятностью 0,6, при одном попадании – с вероятностью 0,3.
1. Найти вероятность того, что в результате трех выстрелов самолет будет
выведен из строя.
2. В результате трех выстрелов самолет не был выведен из строя. Сколько
попаданий вероятнее всего произошло в самолет?
Решение:
а) Пусть события Н1, Н2, Н3, Н4 обозначают, что в самолёт попадут: ни разу, 1 раз, 2 раза и три раза соответственно, а событие А – самолет выведен из строя. Тогда:
P(H1)= |
0,5*0,4*0,3=0,06 |
P(A/H1)= |
0 |
P(H2)= |
0,5*0,4*0,3+0,5*0,6*0,3+0,5*0,4*0,7=0,29 |
P(A/H2)= |
0,3 |
P(H3)= |
0,5*0,6*0,3+0,5*0,4*0,7+0,5*0,6*0,7=0,44 |
P(A/H3)= |
0,6 |
P(H4)= |
0,5*0,6*0,7=0,21 |
P(A/H4)= |
1 |
События Н1, Н2, Н3 и Н4 образуют полную группу, поэтому вероятность того, что самолет выведен из строя в результате трех выстрелов, определим по формуле полной вероятности:
|
или 56,1%
б) Пусть А - самолет не был выведен из строя при тех же гипотезах. Тогда:
-
P(A/H1)=
1-
0
=
1
P(A/H2)=
1-
0,3
=
0,7
P(A/H3)=
1-
0,6
=
0,4
P(A/H4)=
1-
1
=
0
Т.к. самолет не был выведен из строя, т.е. событие A произошло, то вероятности гипотез определим по формуле Байеса
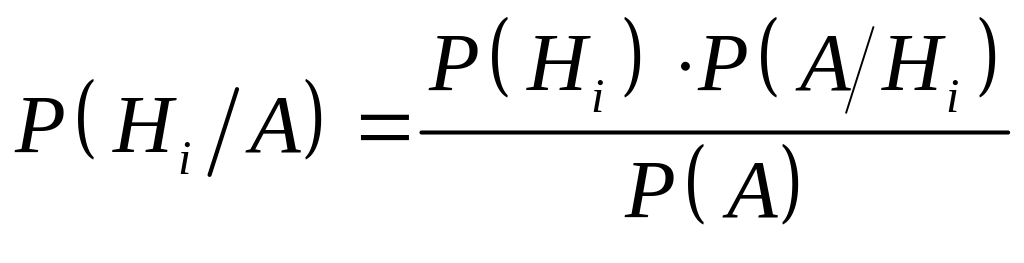
= |
0,06*1+0,29*0,7+0,44*0,4+0,21*0=0,439 |
![]()
![]()
![]()
![]()
Таким образом, вероятнее всего в самолет произошло 1 попадание.
Задание №3.
Согласно статистическим данным в городе N в среднем 17% открывающихся новых предприятий прекращают свою деятельность в течение года.
1. Какова вероятность того, что из 7 наугад выбранных новых предприятий города N к концу года деятельности останется:
а) ровно 5;
b) более 5;
с) менее 5;
d) хотя бы одно предприятие?
2. Вычислить вероятность того, что из ста вновь открытых предприятий в
городе N к концу года прекратят свою деятельность:
а) 14;
b) не менее 14;
с) не более 20;
d) не менее 12, но не более 22 предприятий.
Решение:
1. Какова вероятность того, что из 7 наугад выбранных новых предприятий города N к концу года деятельности останется:
n=7 p=0,83 q=0,17
Значение n<10 , поэтому для расчетов воспользуемся формулой Бернулли:
![]()
a) ровно 5:
![]() или
23,9%
или
23,9%
b) более 5:
P(более 5)=P7(6;7) = P7(6)+P7(7)
![]()
![]()
Тогда:
P(более 5)= 0,389+0,271=0,66 или 66%
c) менее 5:
P(менее 5)=1-P(не менее 5)=1-P7(5;7)=1-(0,239+0,389+0,271)=0,1 или 10%
d) хотя бы одно предприятие:
P(хотя бы 1)=1-P(ни одного)=1-P7(0)
![]()
Тогда
P(хотя
бы 1)=![]() или 100%
или 100%
2. Вычислить вероятность того, что из ста вновь открытых предприятий в городе N к концу года прекратят свою деятельность:
n=100 p=0,17 q=0,83
Значение n=100 достаточно велико, поэтому для расчетов воспользуемся локальной и интегральной формулами Лапласа:
a) 14:
![]() ,
где
,
где
![]() ,
а (x)
– локальная функция Лапласа
,
а (x)
– локальная функция Лапласа
![]()
По таблице находим,
что
(-0,8)=
(0,8)=0,2897,
![]() или 7,71%
или 7,71%
b) не менее 14, т.е. от 14 до 100
Pn(k1;k2)Ф(x2)-Ф(x1),
где
![]() и
и
![]() ,
а Ф(x)
- интегральная функция Лапласа
,
а Ф(x)
- интегральная функция Лапласа
![]() ,
,
![]()
По таблице значений функции Ф(x) находим, что Ф(-0,8)=-0,2881, а Ф(22,1)=0,5,
P100(12;100)0,5+0,2881=0,7881 или 78,81%
c) не более 20, т.е. от 0 до 20
![]() ,
,
![]()
По таблице значений функции Ф(x) находим, что Ф(-4,53)=-0,5, а Ф(0,8)=0,2881,
P100(0;18)0,2881+0,5=0,7881 или 78,81%
d) не менее 12, но не более 22:
![]() ,
,
![]()
По таблице значений функции Ф(x) находим, что Ф(-1,33)=-0,4082, а Ф(1,33)=0,4082,
P100(10;20)0,4082+0,4082=0,8164 или 81,64%
Задание №4.
Два
бухгалтера независимо друг от друга
заполняют одинаковые ведомости. Первый
бухгалтер допускает ошибки в среднем
в 7%, второй – в 13% всех документов.
Количество заполненных ведомостей
первым бухгалтером равно 3, вторым – 0.
Рассматривается случайная величина
(с.в.)
![]() – число ведомостей, заполненных двумя
бухгалтерами без ошибок.
– число ведомостей, заполненных двумя
бухгалтерами без ошибок.
1. Составить ряд распределения с.в. и представить его графически.
2. Найти функцию распределения с.в. и построить её график.
3. Вычислить математическое ожидание (среднее значение) М , дисперсию
D
и среднее квадратическое (стандартное)
отклонение
![]() (
).
(
).
4.
Определить вероятности: а) Р![]() ;
b)
Р
;
b)
Р![]() ;
c)
Р
;
c)
Р![]()
Решение:
Т.к. ведомости заполняются только одним бухгалтером, то определим возможные значения случайной величины Х и их вероятности по формуле Бернулли:
q=0,07, Р=1-0,07=0,93
Х=0:
![]()
Х=1:
![]()
Х=2:
![]()
Х=3:
![]()
Проверка:
0,000343+0,013671+0,181629+0,804357=1
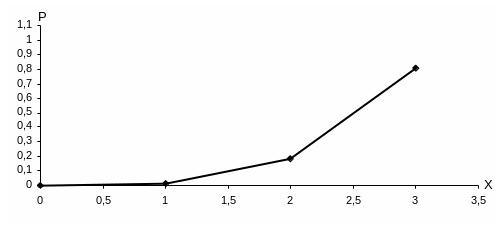
Запишем ряд распределения
-
x
0
1
2
3
p
0,0003
0,0137
0,1816
0,8044
Изобразим ряд распределения графически в виде полигона
2) Составим функцию распределения:

Построим график функции распределения
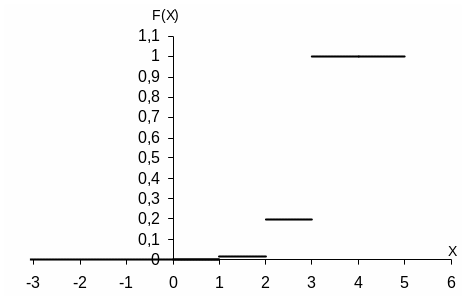
3) Математическое ожидание и дисперсия находятся по формуле:
![]()
![]()
D(X)=7,9794-2,792=0,1953
![]()
4) Найдем требуемые вероятности:
Р(X<MX)=Р(X<2,79)=F(2,79)=0,1956
Р(XMX+1)=1–Р(X<3,79)=1–F(3,79)=1–1=0
![]() =P(2,3481<X<3,2319)=1-0,1956=0,8044
=P(2,3481<X<3,2319)=1-0,1956=0,8044
