3.3 Лабораторна робота 6

Для двоопорної рами побудувати епюри повздовжніх, поперечних сил та згинальних моментів, і перевірити раму на міцність, якщо []=160 МПа.

Вихідні дані вибрати з таблиць 3.3, 3.4 і рисунка 3.15.

Таблиця 3.3

Величина	Значення величини відповідно до першої цифри номера варіанта
	0	1	2	3	4	5	6	7	8	9
q1, кН/м	100	300	150	250	200	100	250	150	200	450
M, кН·м	400	200	300	100	400	300	300	100	300	400
a, м	0,6	0,5	0,7	0,9	0,8	1,0	0,4	0,7	0,8	0,6
b, м	1,0	0,8	0,5	0,7	0,4	1,3	0,8	0,9	0,7	0,8

Таблиця 3.4

Величина	Значення величини відповідно до другої цифри номера варіанта
	0	1	2	3	4	5	6	7	8	9
c, м	0,5	0,6	0,9	0,8	0,7	1,0	0,5	0,4	0,4	1,2
d, м	1,5	1,3	1,4	2,0	2,4	2,8	3,0	1,5	3,4	4,0
q2, кН/м	300	150	100	200	150	250	100	200	250	150

Рисунок 3.15

Рисунок 3.15, аркуш 2

Рисунок 3.15, аркуш 3

Указівки до виконання лабораторної роботи 6

1 Поділяємо стрижень на кінцеві елементи. Нумеруємо елементи, що вийшли, і вузли (зручно брати як кінцеві елементи ділянки стрижня).

2 Обчислюємо матрицю жорсткості кожного з елементів

,

де J_{хi –} момент інерції перерізу i-го елемента,

_i – довжина i-го елемента,

Е – модуль пружності.

3 Записуємо матрицю напрямних косинусів для кожного з елементів:

,

де  – кут нахилу кінцевого елемента до горизонтальної осі.

4. Формуємо матрицю жорсткості конструкції як ансамбль матриць жорсткості кінцевих елементів, з яких складається конструкція. Її порядок дорівнює кількості вузлів, яка помножена на 3.

5 Записуємо систему рівнянь виду:

де К – матриця жорсткості конструкції в цілому;

– вектор кутів повороту всіх вузлів;

– вектор вузлових навантажень.

На ділянках де діє розподілене навантаження вважається, що його дія рівносильна впливу вузлових навантажень: у лівому вузлі P_i = ql/2, M_i = ql²/12, а у правому P_J = ql/2, M_J = – ql²/12 (рис. 3.16, б).

Рисунок 3.16

6 З вирішення системи рівнянь знаходяться переміщення і кути повороту вузлів.

7 Визначити величини поперечних сил Р_i і згинальних моментів M_i:

Побудувавши графік зміни поперечних сил і згинальних моментів, за довжиною стрижня, отримаємо епюри повздовжніх, поперечних сил і згинальних моментів.

8. З умови міцності визначити необхідний момент опору перерізу:

,

де – осьовий момент опору перерізу елемента;

[] – допустимі нормальні напруження.

8. Визначити необхідні розміри поперечного перерізу, враховуючи, що

.

Приклад виконання лабораторної роботи 6

Для рами, показаної на рисунку 3.17, побудувати епюри подовжніх, поперечних сил і згинальних моментів. Визначити максимальні нормальні напруження, якщо поперечний переріз рами прямокутного перерізу – h=10 см, b=6 см.

Розв’язок. Нумеруємо вузли і елементи. Визначаємо геометричні характеристики перерізу (рис. 3.18):

F=6·10=60 см²,

см⁴.

Рисунок 3.18 – Поперечний переріз рами

Визначаємо жорсткості елементів при розтяганні та згинанні:

МН, МН·м².

Переходимо до обчислення матриць жорсткості елементів.

1-й елемент (входять вузли 1-2):  = 90 .

Матриця напрямних косинусів для нього

·

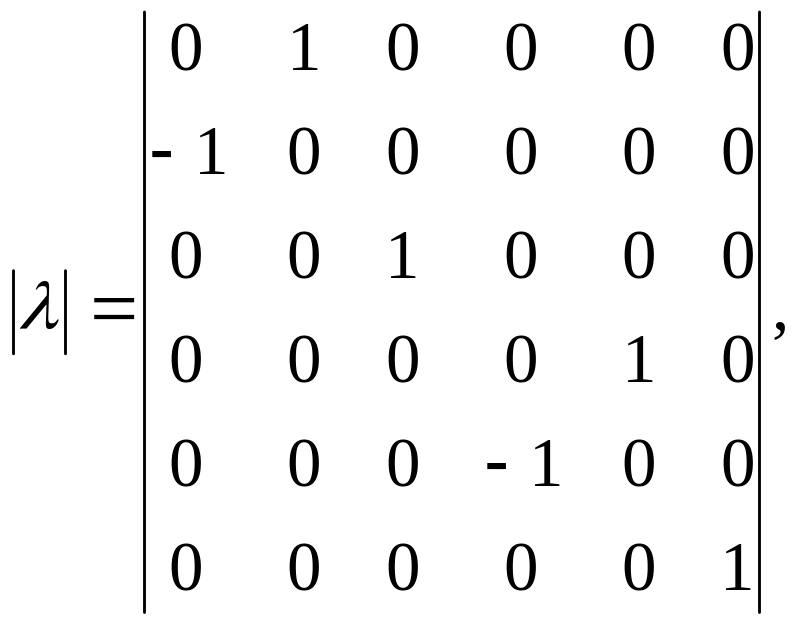
2-й елемент (вузли 2-3):  = 0 .

,

Оскільки || є одиничною матрицею, то .

Тепер формуємо матрицю жорсткості конструкції. У рамі маємо три вузли, кожен з яких має три степені вільності. Отже, матриця жорсткості конструкції має розмірність 9х9.

При записі вектора вузлових сил враховуємо, що на 1-й елемент діє розподілене навантаження. Отже, у першому і другому вузлах мають бути прикладені сили в горизонтальному напрямку ql/2=8·3/2=12 кН і моменти ql²/12= – 8·32/12= – 6 кН·м і ql²/12=8·32/12= 6 кН·м.

У третьому вузлі прикладений момент 15 кН·м. Оскільки коефіцієнти матриці жорсткості мають одиниці виміру меганьютон (МН) і метр (м), то вектор вузлових сил умножаємо на 10^-3.

Граничні умови: .

Після урахування граничних умов маємо:

.

Після вирішення системи рівнянь отримаємо:

Визначаємо зусилля на кінцях елементів за формулою

1-й елемент:

Набудемо значень вектора вузлових навантажень на кінцях елемента (сили – у меганьютонах (МН), моменти – у меганьютон-метрах (МН·м)).

Перевіряємо рівновагу елемента (рис. 3.19, а):

-12,2-11,8+3·8=0; -24+24=0,

-7,7+7,7=0,

-5,5-8·3·1,5+11,8·3+6,2=0; -41,5+41,6=0.

Будуємо епюри подовжніх (рис. 3.19, б) сил, поперечних сил (рис. 3.19, в) і епюру згинальних моментів (рис. 3.19, г).

М_к= – 11,8·1,475 + 5,5 + 8·1,475·1,475/2= – 3,1 кН·м.

а – елемент з навантаженнями; б – епюра повздовжніх сил;

в – епюра поперечних сил; г – епюра згинальних моментів

Рисунок 3.19 – Елемент 1

2-й елемент:

Перевіряємо рівновагу другого елемента:

-11,75+11,75=0,

7,7-7,7=0,

5,5-7,7·2+10=0,

15,5-15,4  0.

Зістикувавши епюри за всіма елементами (рис. 3.14 і 3.20), одержуємо остаточні епюри (рис. 3.21).

Визначаємо максимальні нормальні напруження.

Небезпечним є переріз, де М_мах=10 кН·м.

У цьому перерізі N=7,7 кН.

,

.

а – елемент з навантаженнями; б – епюра повздовжніх сил;

в – епюра поперечних сил; г – епюра згинальних моментів

Рисунок 3.20 – Елемент 2

а – епюра повздовжніх сил; б – епюра поперечних сил;

в – епюра згинальних моментів

Рисунок 3.21 – Остаточні епюри для рами