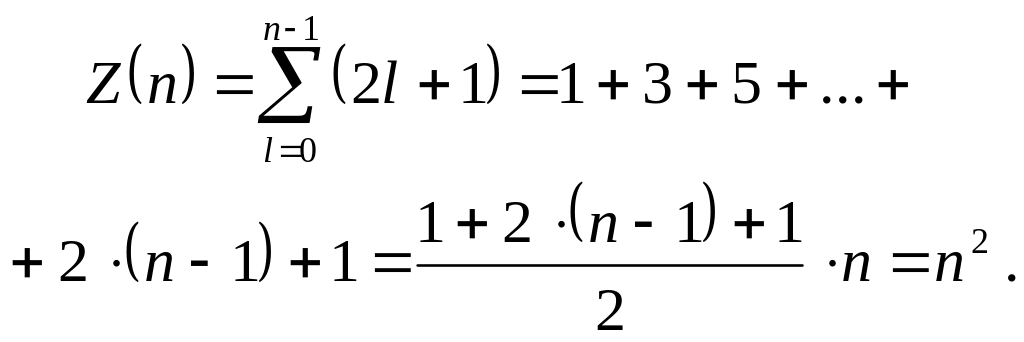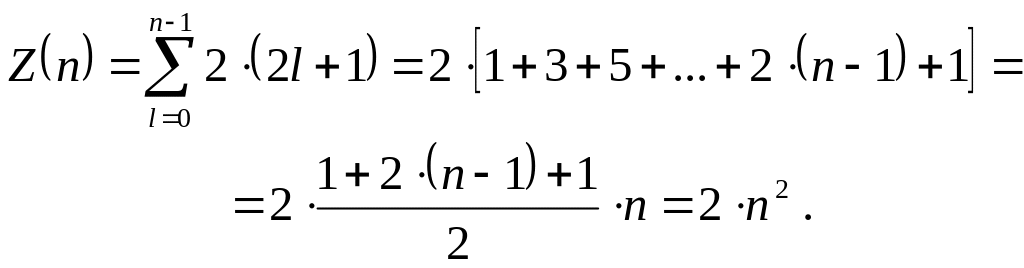Атом водню у квантовій механіці

У квантовій механіці задача про атом водню (крім його простої структури) є однією із основних ще і тому, що задача про рух електрона у полі центральних сил може бути поширена і на воднеподібні системи, які складаються з ядра із зарядом Ze і одного електрону (наприклад, іони Не⁺, Li²⁺ та інші). Потенціальна енергія взаємодії електрона із ядром воднеподібного атома має вигляд:

де r – відстань від електрона до ядра атома, Z – порядковий номер елемента в таблиці Менделєєва. Відповідно, стаціонарне рівняння Шредінгера для тривимірного руху електрона на-

вколо ядра воднеподібного атома має вигляд:

Оскільки електричне поле воднеподібного атома має сферичну симетрією, вирішувати таке рівняння поцільно у сферичних координатах (r,,) методом роз-

ділення змінних. Це досить складна задача, але якісні її результати такі.

1. Таке рівняння має кінцеві, однозначні і безперервні рішення не завжди, а лише при певних значеннях параметрів, які входять у нього. Одним із цих параметрів є повна енергія електрона Е. Рух електрона у атомі, що задовольняє цьому рівнянню, може відбуватись тільки при певних (дискретних) негативних значен-

нях енергії: Це - власні значення енергії електрона в атомі, які відповідають власним хвильовим функціям n, одержаним із рі-

шення рівняння. Тут n=1,2,3,…- головне квантове число. Рівень енергії Е₁, відповідний мінімальному значенню енергії (n=1), називають основним, а всі інші Е_n (n=2,3,4,…) – збудженими. Якщо енергія електрона Е0, його рух називається зв'язаним, оскільки він знаходиться усередині гіперболічної потенціальної ями. При зростанні n, збуджені енергетичні рівні розташовуються щільніше. Коли повна енергія електрона Е стає позитивною (тобто, його кінетична енергія перевищує потенціальну енергію тяжіння до ядра), то електрон стає вільним, а його енергетичний спектр стає суцільним – енергія електрона може набувати довільних значень.

2) Із рівняння Шредінгера виходить, що кожен стаціонарний стан електрона в атомі характеризується трьома квантовими числами: n – головним, l – орбітальним, m – магнітним. Ці квантові числа визначаються властивостями хвильових функцій – їх неперервністю, однозначністю і скінченністю у всьому об'ємі. Орбітальне квантове число l визначає модуль орбітального моменту імпульсу елект-

рона, який може набувати лише дискретних значень, тобто квантується згідно із формулою: При певному значенні n орбітальне квантове число l може на-

бувати значень 0, 1, 2,…, (n-1) (тобто, всього n-значень). Магнітне квантове число m визначає проекції орбітального моменту імпульсу на деякий довільно вибраний напрямок зовнішнього магнітного поля, які також можуть набувати лише дискретних значень, тобто квантуються згідно формулі: L_z=ħm. При певному значенні l, магнітне квантове число може набувати значення m=0, 1, 2,…, l, (всього (2l+1) - значення). Орбітальним гіромагнітним відношенням електрона називають відношення магнітного моменту електрона p_m до його механічного моменту імпульсу L. Підставивши відповідні значення, для орбітального руху елект-

рона одержимо: де е – заряд електрона, m0 – його маса. Підставивши значення L, отримаємо ви-

раз длявизначення дозволених значень орбітального магнітного моменту:

де величину eћ/2m0 називають магнетоном Бора і позначають μВ. Отже, магнітні моменти електрона при його орбітальному

русі навколо ядра також набувають дискретних значень. Для проекції орбітального магнітного моменту електрона на напрямок зовнішнього магнітного поля має-

мо: де m – магнітне квантове число, яке може набувати позитивних і негативних значень.

Таким чином, рух електрона в атомі є «строго регламентованим». Енергія електрона залежить від головного квантового числа, що визначає розміри орбіти, орбітального квантового числа, що визначає форму орбіти, і магнітного квантового числа, що визначає її орієнтацію у просторі. Кожному власному значенню енергії Е_n (окрім Е₁) відповідає декілька власних хвильових функцій _nlm, відмінних значеннями l і m. Тому атом може мати одне і те ж значення енергії, знаходячись при цьому у різних станах, званих виродженими. Кількість станів із однаковою енергією, або кратність виродження енергетичних рівнів може бути

визначена формулою: Вірогідність виявлення електрона в різних частинах атома різна. Електрон при своєму русі неначе «розмазаний» по всьому об'єму атома, утво-рюючи електронну хмару, густина якої характе-

ризує вірогідність знаходження електрона в різних точках об'єму. Квантові числа n і l характеризують розмір і форму електронної хмари, а квантове число m характеризує її орієнтацію у просторі.

Голландські фізики Уленбек і Гаудсміт у 1925 році висунули гіпотезу, згідно якої електрон володіє не тільки орбітальним, але і власним механічним моментом імпульсу, названому спіном. Для наочності, наявність у електрона спіну можна уявити його обертанням навколо своєї осі (по-англійськи «to spin» – обертатись, вертітись). Поняття спіну електрона (і інших мікрочастинок) введене для пояснення результатів дослідів Штерна і Герлаха, які спостерігали розщеплювання вузького пучка атомів водню у неоднорідному магнітному полі на дві частини. Спін – чисто квантова величина, у неї немає класичного аналогу: це внутрішня, невід'ємна властивість електрона, як його заряд або маса. Згідно висновкам квантової механіки, спін електрона, і його проекція на напрям зовнішнього магнітного поля квантуються. По аналогії із орбітальним рухом, спін і його проекція можуть

набувати значень: де S – спінове квантове число, ms - спінове магнітне квантове число. Оскільки ms може приймати всього

(2S+1)-значення, а розщеплення пучка відбувалось на 2 компоненти (можливі дві орієнтації спина у магнітному полі), із умови (2S+1)=2 визначили значення спінового квантового числа S=1/2. Спінове магнітне квантове число m_s може набувати два значення m_s=1/2. Дослідним шляхом було встановлено, що гіромагнітне від-

	ношення для спінових моментів у два рази більше, ніж для орбітальних моментів електрона, а саме: Звідки, спіновий магнітний момент електрона складає:
		де B - магнетон Бора, який є одиницею виміру магнітних моментів. Про- екція спінового магнітного моменту на вісь z може набувати значень: Спінові механічний та магнітний мо-менти електрона виявляються не тіль

ки у магнітних властивостях речовини, але і в інших явищах, тому можна говорити про спінове магнітне квантове число m_s, як про четвертий тип квантового числа, що визначає поведінку електронів у атомах.

Якщо при перестановці частинок місцями хвильова функція не змінює знак, вона називається симетричною, а якщо змінює – антисиметричною. Симетрія хвильових функцій визначається спіном частинок. Частинки із нульовими або цілими спінами (-мезони, фотони) описуються симетричними хвильовими функціями, підлягають статистиці Бозе-Ейнштейна і називаються бозонами. А частинки із напівцілими спінами (електрони, протони) описуються антисиметричними хвильовими функціями, підлягають статистиці Фермі-Дірака і називаються ферміонами. Залежність характеру симетрії хвильових функцій системи тотожних частинок від їх спину теоретично обгрунтована швейцарським фізиком Паулі. Узагальнюючи дослідні дані, він сформулював принцип (принцип Паулі). Оскільки стан електрона у атомі однозначно визначається чотирма квантовими числами, то згідно принципу Паулі, два електрони у одному і тому ж атомі повинні розрізнятися значеннями, принаймні, одного квантового числа, тобто Z(n, l, m, m_s)=0 або 1. Максимальна кількість електронів, які знаходяться у станах, визначених головним квантовим числом n (кратність виродження енергетичного рівня Е_n із урахуванням спіну електрона) визначається формулою:

Сукупність електронів у багатоелектрон-ному атомі, які мають однакове головне квантове число n, називають електрон-ним шаром. Сукупність електронів у кожному шарі, відповідних певному значен-

ню орбітального квантового числа l,називають електронною оболонкою. Кількість електронів у оболонках визначається магнітним m і спіновим m_s квантовими числами. Позначення електронних шарів і оболонок взяті із спектроскопії, а наповнення їх електронами приведене у таблиці:

Головне кван- тове число n	1	2		3			4				5
Символ элект- ронного шару	K	L		M			N				O
Число электро- нів в шарі	2	8		18			32				50
Орбітальне ква-нтове число l	0	0	1	0	1	2	0	1	2	3	0	1	2	3	4
Символ электронної оболонки	1S	2S	2p	3S	3p	3d	4S	4p	4d	4f	5S	5p	5d	5f	5g
Число электро-нів у оболонці	2	2	6	2	6	10	2	6	10	14	2	6	10	14	18

Принцип Паулі, який лежить у основі систематики заповнення електронних станів в атомах, дозволяє пояснити Періодичну систему елементів Д.І.Менделєєва – фундаментального закону природи, що є основою сучасної хімії, атомної і ядерної фізики. Оскільки хімічні і деякі фізичні властивості пояснюються зовнішніми (валентними) електронами у атомах, то періодичність властивостей елементів мусить бути зв'язана із певною періодичністю у розташуванні електронів в атомах, яка відповідає принципу Паулі і стає цілком зрозумілою.

ТЕСТОВІ ЗАВДАННЯ З РОЗДІЛУ “ЕЛЕМЕНТИ КВАНТОВОЇ МЕХАНІКИ”