Примеры решения задач

Задача 1.

Максимальный заряд на обкладках конденсатора колебательного контура 10^-6 Кл. Амплитудное значение силы тока в контуре 10^-3А. Определите период колебаний. Потерями проводников можно пренебречь.

Решение.

Согласно закону сохранения энергии максимальное значение электрического поля конденсатора равно максимальному значению энергии магнитного поля катушки:

,

отсюда:

или

Следовательно,

Ответ: 6,3мс.

Задача 2.

Колебательный контур состоит из конденсатора емкостью 5мкФ и катушки индуктивностью 0,2Гн. Определить максимальную силу тока в контуре, если максимальная разность потенциалов на обкладках конденсатора 90В. Сопротивлением контура R пренебречь.

Решение.

Так как , то 0 и в контуре будут незатухающие колебания, при этом:

Сила тока есть производная от заряда по времени, поэтому для силы тока в контуре получим уравнение:

Величина является амплитудным, т.е. максимальным значением тока в контуре. Учитывая, что:

и ,

тогда:

Вычисляя, получаем:

Ответ: 1,45А.

Задача 3.

Колебательный контур имеет емкость С, индуктивность L и активное сопротивление R. Найти через сколько колебаний амплитуда тока в этом контуре уменьшится в е раз.

Решение.

Амплитуда тока ( ~ ) уменьшается в раз за время За это время совершится колебаний:

Учитывая, что и получаем:

Ответ:

Задача 4.

Колебательный контур имеет емкость 1,3·10^-9Ф и индуктивность 5·10^-3Гн. Логарифмический декремент затухания 0,005. За сколько времени энергия в контуре уменьшится в 10 раз?

Решение.

Энергия в колебательном контуре пропорциональна (или , или ), следовательно. ~ .

По условию

10.

Отсюда 10,

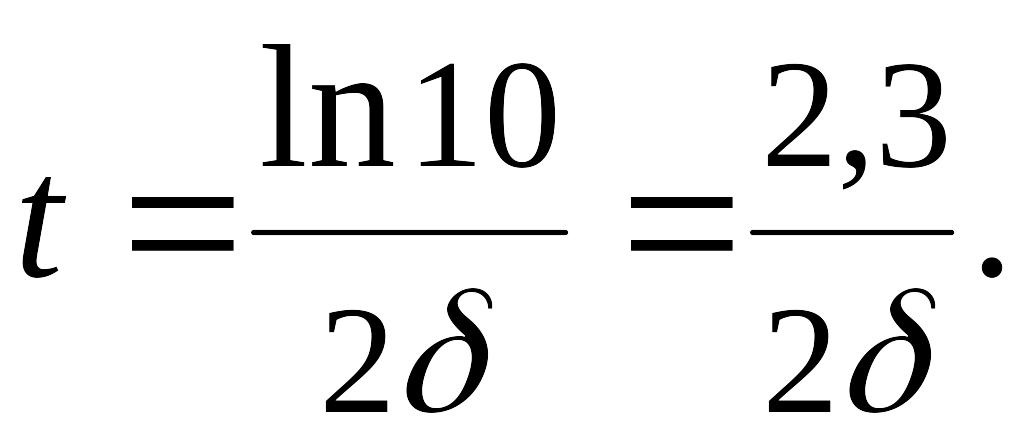
Логарифмический декремент затухания:

Находим коэффициент затухания:

где

Тогда искомое время

Произведя вычисления, получим:

мс.

Ответ: 3,6мс.

Задача 5.

Цепь переменного тока, содержащая последовательно соединенные конденсатор С, катушку L с активным сопротивлением R, подключена к внешнему переменному напряжению, частоту которого можно менять, не меняя его амплитуды. При частотах и амплитуды силы тока в цепи оказались одинаковыми. Найти резонансную частоту тока.

Решение.

Амплитуда силы тока:

Амплитуды будут одинаковыми при условии:

(*)

Максимуму резонансной кривой тока соответствует частота, равная собственной частоте:

Пусть (тот же результат, если ) равенство (*) запишем без модулей:

или

Сократив обе части равенства на , получим:

1

Отсюда резонансная частота тока:

Ответ:

Задача 6

Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами площадью S=100см^? каждая и катушки с индуктивностью 1мкГн, резонирует на волну длиной 10м. Определить расстояние d между пластинами конденсатора.

Решение.

Расстояние между пластинами конденсатора можно найти из формулы электроемкости плоского конденсатора:

где - диэлектрическая проницаемость среды, заполняющей конденсатор,

откуда:

(*)

Из формулы Томсона, определяющей период колебаний в электрическом контуре:

находим электроемкость:

(**)

Неизвестный в условии задачи период колебаний можно определить, зная длину волны , на которую резонирует контур.

Из соотношения , имеем:

Подставив выражения периода Т в формулу (**), а затем электроемкости С в формулу (*), получим:

Произведя вычисления, найдем:

Ответ: 3,14мм.

Задача 7.

Напишите уравнение плоской электромагнитной волны, распространяющейся вдоль оси в однородной среде ( ), если при 0 и 0 напряженность ее электрического поля 5В/м. Амплитуда волны 5В/м, длина волны 1м.

Решение.

Уравнение волны с учетом начальной фазы :

Определим угловую частоту волновое число и начальную фазу .

Волновое число:

Скорость волны

где - скорость электромагнитной волны в вакууме.

Отсюда получаем выражение для угловой частоты:

Вычисляя, находим:

Начальную фазу определяем из начальных условий: при 0 и 0,

Следовательно, 1,

Уравнение плоской электромагнитной волны:

Ответ:

Домашнее задание:

[Л-2] – 14.1, 14.3, 14.5, 14.7, 14.9, 14.10, 14.13, 14.15;

[Л-3] – 3.156, 3.157, 3.159, 3.160;

[Л-4] – 4.40, 4.42, 4.45, 4.75, 4.77, 4.78, 4.79.