Вопросы для ответа у доски

1. Индуктивность в цепи переменного тока.

Зная переменное напряжение, получите формулу для мгновенного значения тока. Покажите, что ток отстает по фазе от напряжения на . Рассмотрите реактивное сопротивление индуктивности и проанализируйте его. От каких величин оно зависит? Используйте метод векторных диаграмм.

2. Емкость в цепи переменного тока.

План изложения вопроса такой же, как для случая индуктивности.

3. Цепь переменного тока, содержащая емкость, индуктивность и сопротивление.

Рассмотрите случай последовательного соединения в цепи переменного тока конденсатора, катушки и сопротивления. Используя метод векторных диаграмм, получите выражение для максимального тока и тангенса угла сдвига фаз между током и напряжением. Проанализируйте их.

Примеры решения задач

Задача 1.

Катушка с индуктивным сопротивлением 500Ом присоединена к источнику переменного напряжения, частота которого 1000Гц. Действующее значение напряжения 100В. Определите амплитуду силы тока I_m в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.

Решение.

Индуктивное сопротивление катушки выражается формулой:

Отсюда

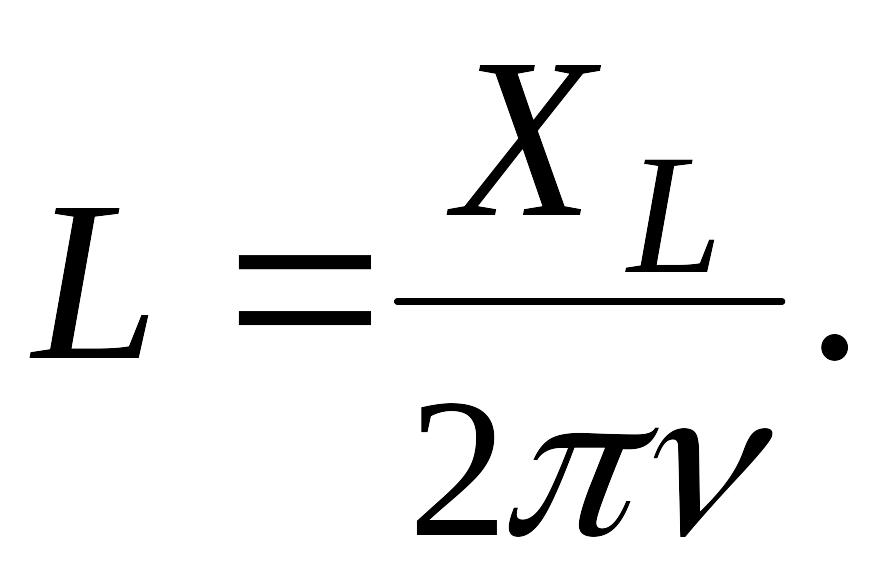
Подставив численные значения, получаем: Гн.

Так как амплитуда напряжения связана с его действующим значением соотношением: то для амплитуды силы тока получаем:

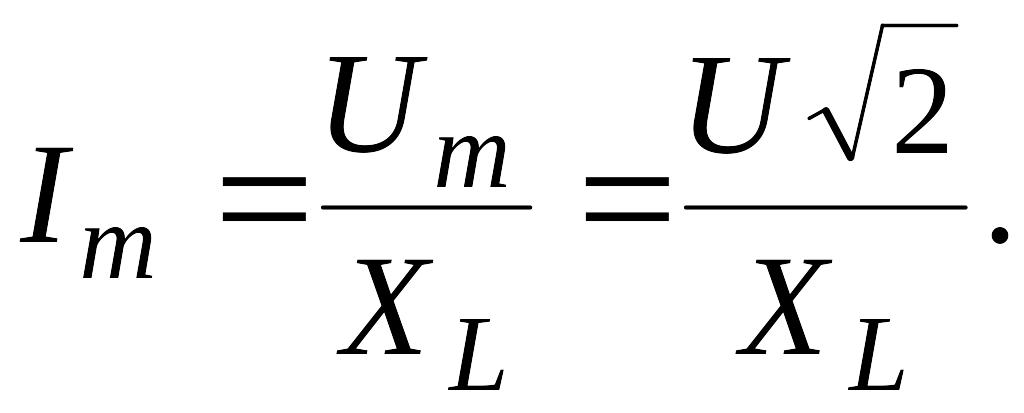
Вычисляя, находим:

Ответ: 0,28А.

Задача 2.

Участок цепи, состоящий из последовательно соединенных конденсатора и активного сопротивления , подключили к внешнему переменному напряжению с амплитудой U_m. При этом амплитуда установившегося тока оказалась равной . Найти разность фаз между током и внешним напряжением.

Решение.

где определяется по формуле:

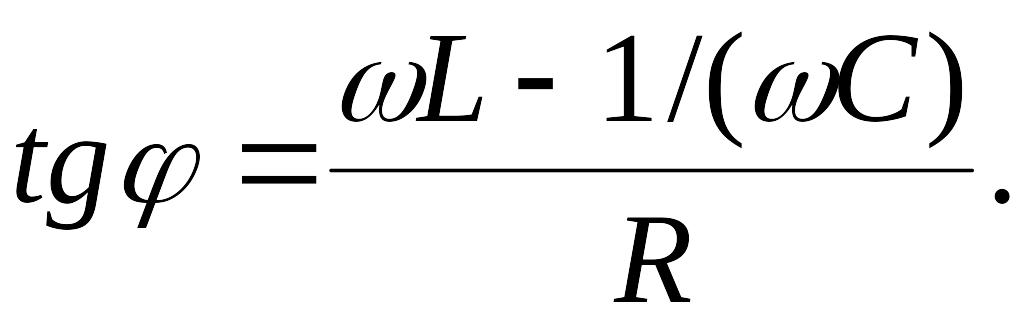
Так как по условию задачи 0, то

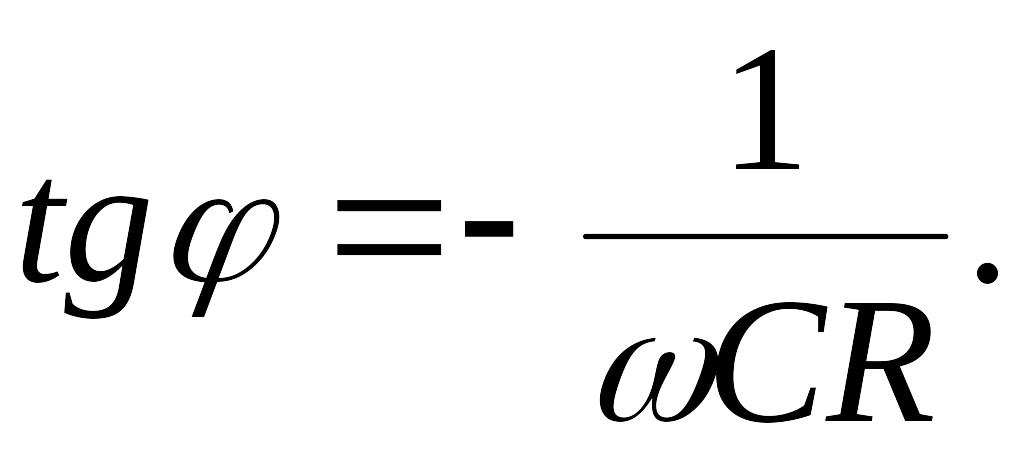
Значение емкости конденсатора С найдем из выражения для амплитуды тока:

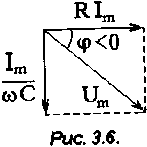
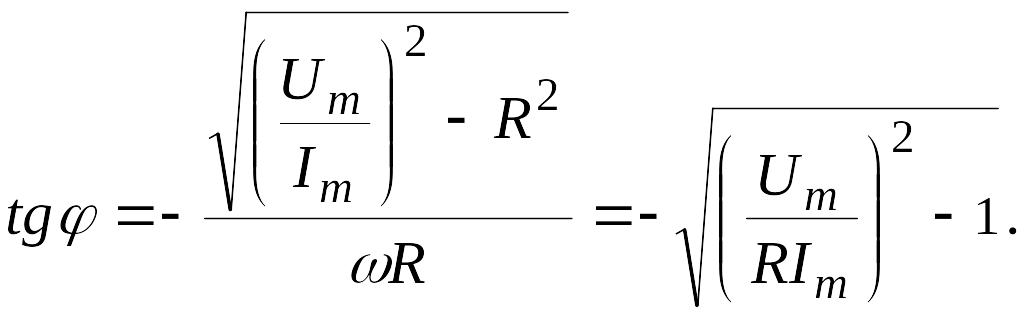
В нашем случае 0, т.е. ток опережает по фазе внешнее напряжение.

Ответ:

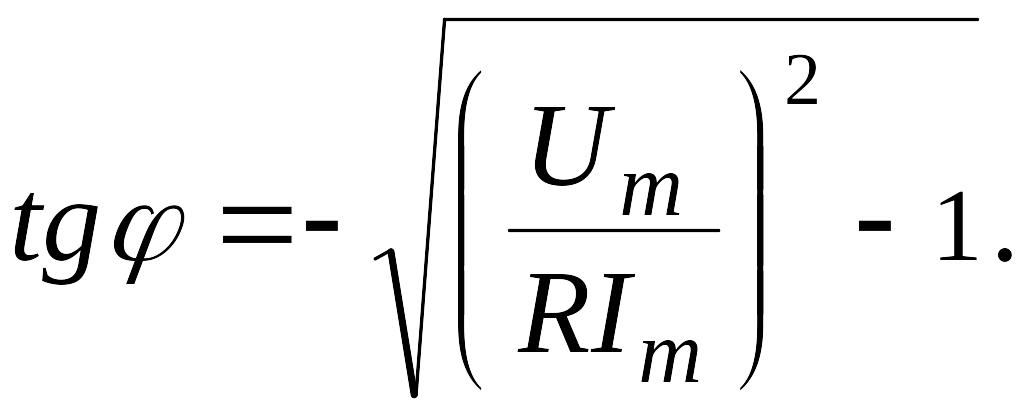
Задача 3.

Сопротивление 10 Ом и катушка с индуктивностью 0,1Гн соединены последовательно. Какую емкость необходимо включить последовательно в цепь, чтобы уменьшить сдвиг фазы между ЭДС и силой тока на 27⁰? Частота изменения ЭДС с частотой 50Гц.

Решение.

Используя метод векторных диаграмм, получаем:

Отсюда:

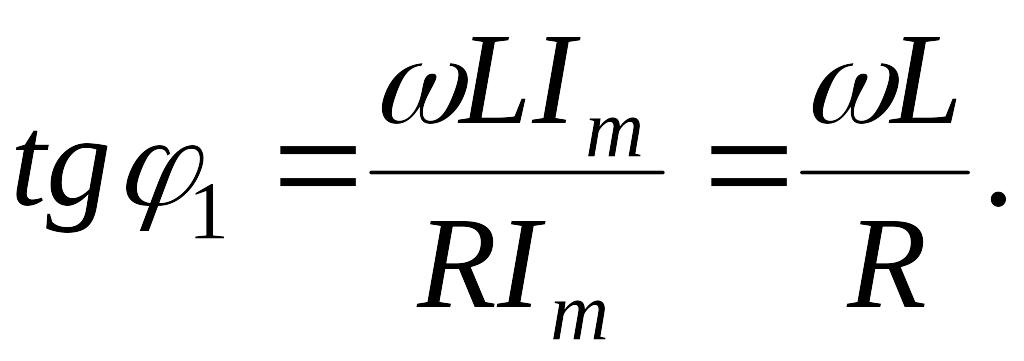
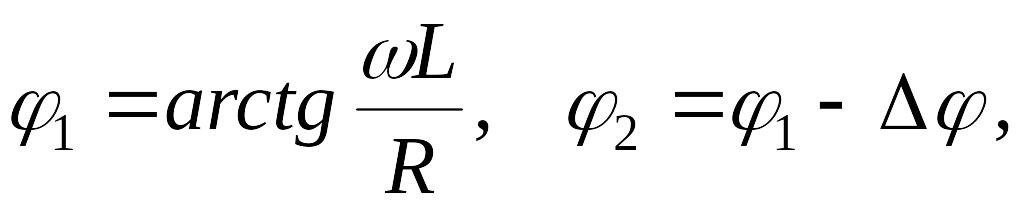
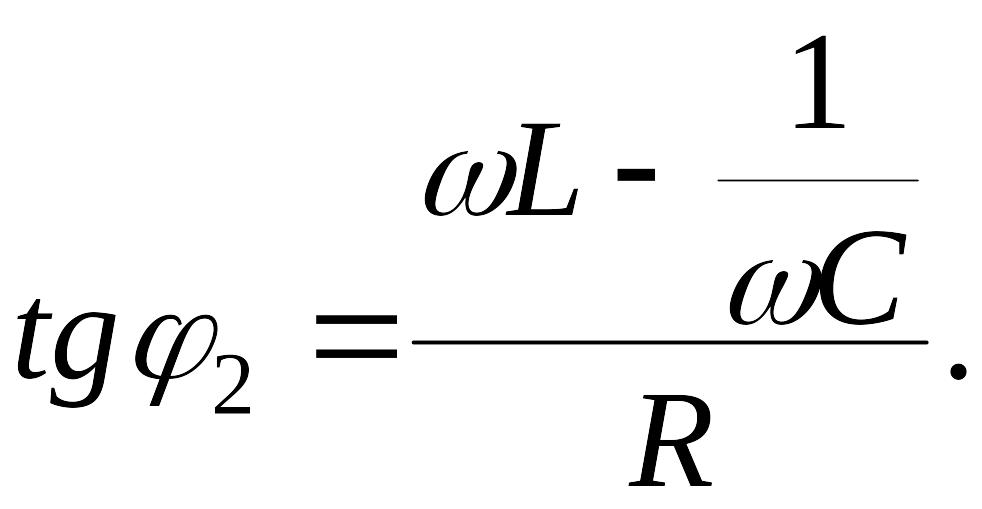
Учитывая, что , определяем неизвестную емкость :

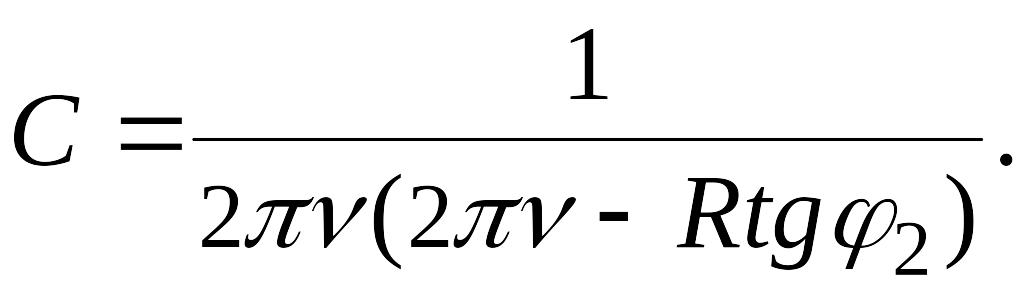
Произведем вычисления:

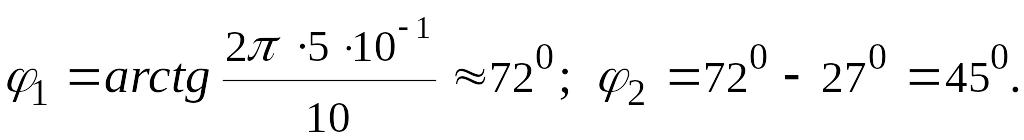Следовательно,

мкФ.

Ответ: 1,5·10²мкФ.

Задача 4.

В цепь переменного тока ( 50 Гц) с действующим напряжением 127В включены параллельно конденсатор емкостью 24мкФ и дроссель индуктивностью 0,6Гц и активным сопротивлением 100Ом. Определите действующее значение подводимого к участку тока.

Д ано:

U=127В

f =50Гц

С=24·10^-6Ф

L =0,6Гн

R = 100Ом

- ?

Решение.

Начертим схему соединения приборов и построим векторную диаграмму токов. При параллельном соединении элементов на каждом из них напряжение одинаковое, поэтому за основное направление возьмем вектор амплитуды напряжения. Амплитуда тока в конденсаторе опережает амплитуду напряжения на , амплитуда тока в дросселе отстает от амплитуды напряжения на угол 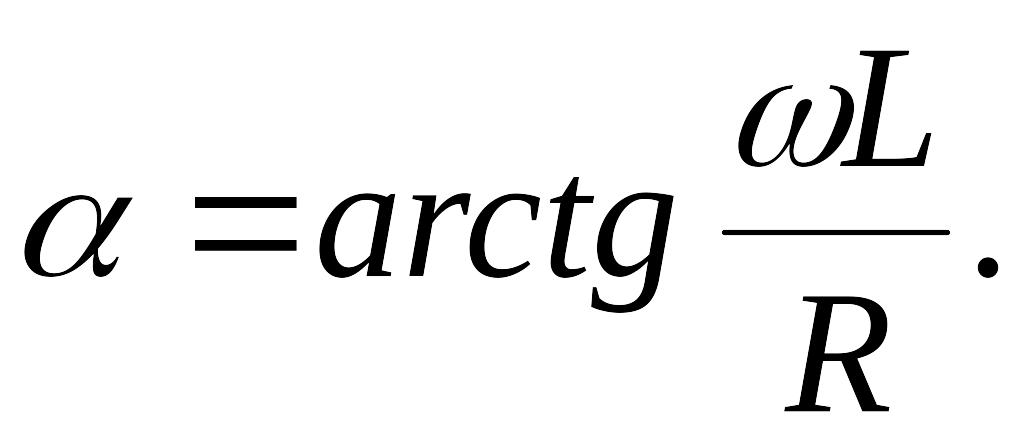Векторная сумма токов и определяет подводимый ток

Из векторной диаграммы очевидно, что

Перейдем к действующим значениям тока:

Токи и найдем, применив закон Ома к каждому участку отдельно:

Вычисляя, получим:

Ответ:

Задача 5.

Вольтметр, подключенный параллельно катушке и конденсатору показывает нуль при значении емкости конденсатора С. Найти значение индуктивности L катушки. Частота переменного питающего напряжения v.

Решение.

Вольтметр показывает нуль при резонансе, т.е. в случае, если:

, где Откуда: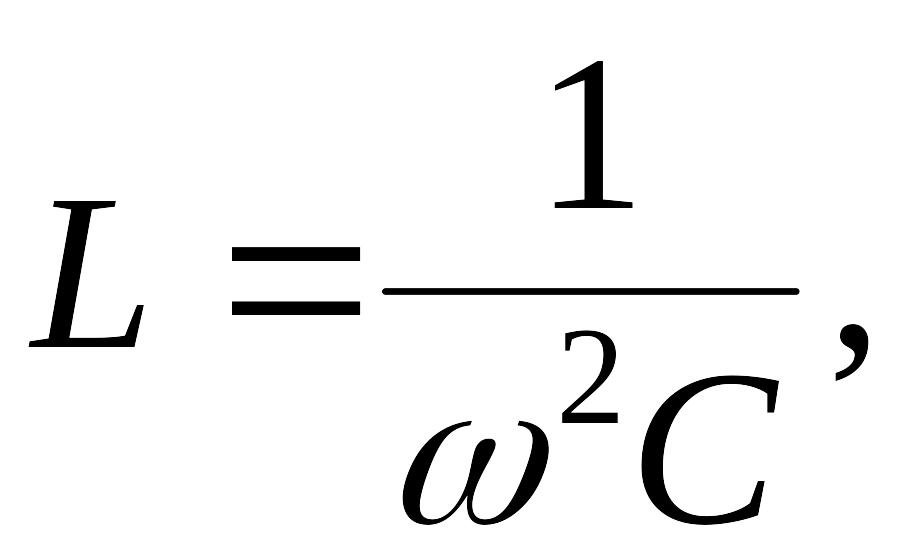

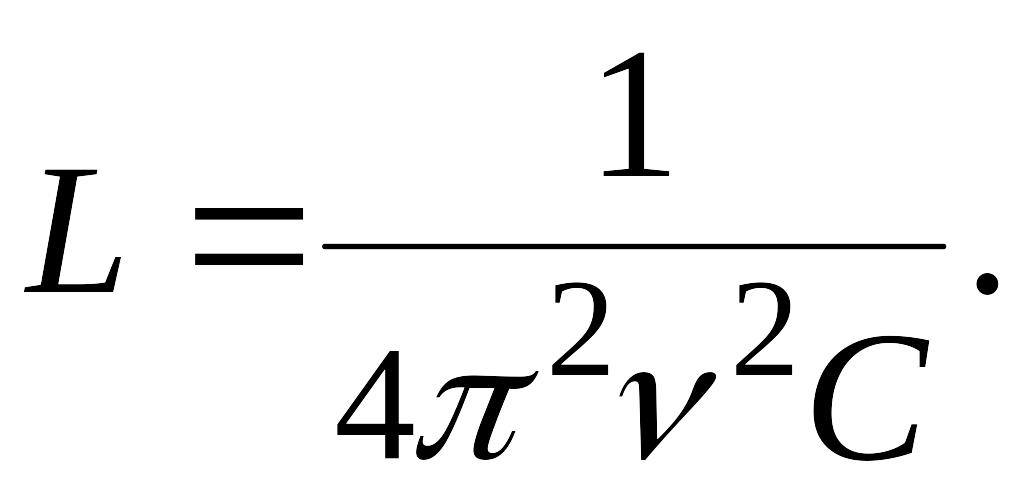
Ответ:

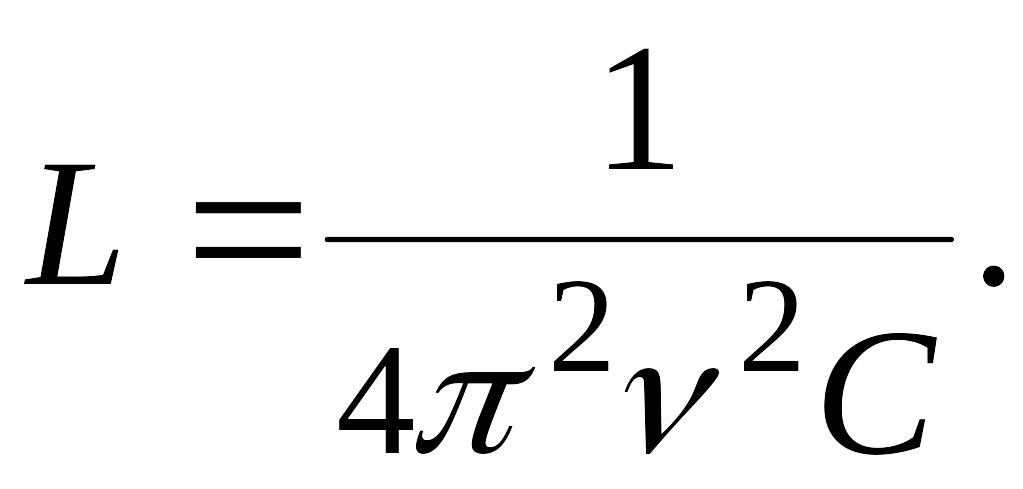
Задача 6.

В цепь переменного тока с действующим напряжением 220В ( 50Гц) включены последовательно конденсатор емкостью 18мкФ, активное сопротивление 10Ом и дроссель индуктивностью 0,6Гн, на котором напряжение опережает ток на угол 60⁰. Определите: а) мощность, выделяемую на каждом из элементов и во всей цепи: б) коэффициент мощности для всей цепи.

Решение.

Мощность, поглощаемая каким-либо участком цепи, определяется квадратом действующего значения тока и активным сопротивлением участка:

Изобразим схему включения приборов и построим векторную диаграмму напряжений. При последовательном соединении через все элементы идет одинаковый ток, поэтому за основное направление возьмем вектор амплитуды тока . Амплитуда напряжения на конденсаторе отстает по фазе от тока на Амплитуда напряжения на дросселе опережает по фазе ток на . Амплитуду напряжения на дросселе разложим на две составляющие: активную (колеблется в фазе с током) и реактивную (опережает ток по фазе на ). Амплитуда полного напряжения в цепи равна векторной сумме напряжений

Амплитуда напряжения, совпадающего по фазе с током:

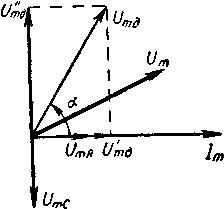
Амплитуда напряжения, опережающего ток на :

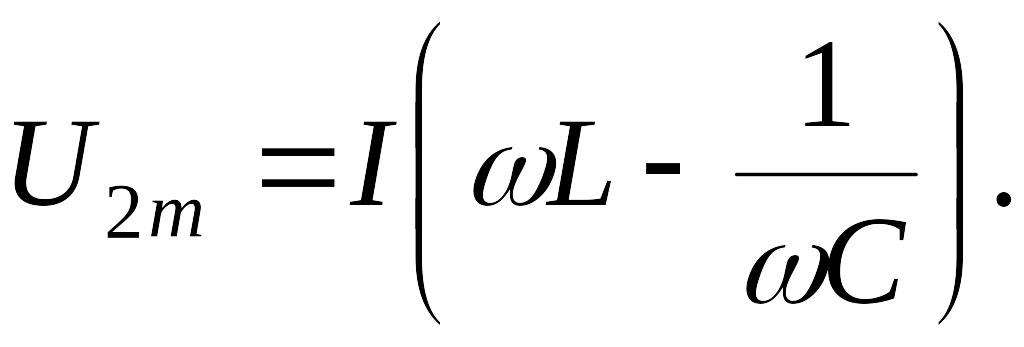
Амплитуда полного напряжения:

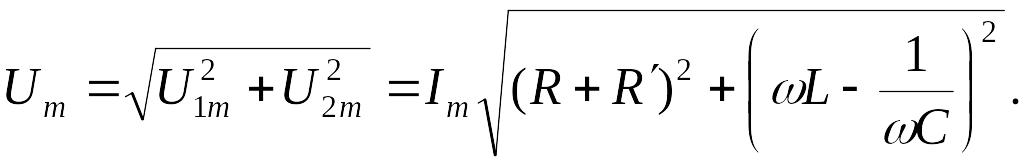
Переходя к действующим значениям напряжения и тока, получаем:

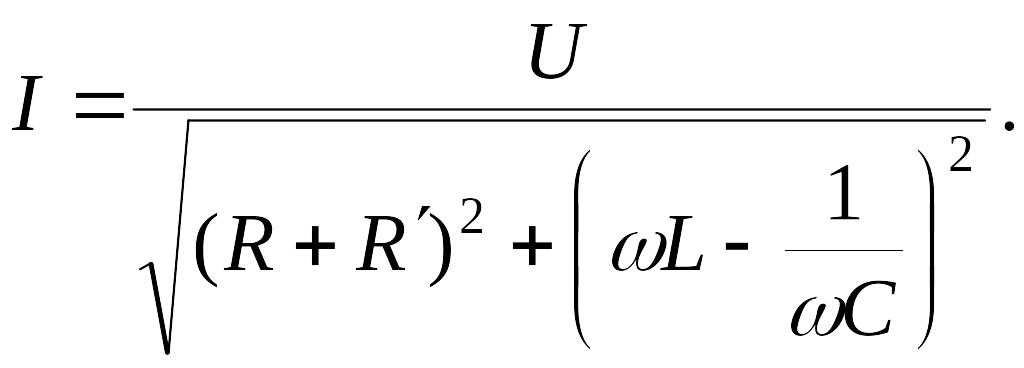
Активное сопротивление дросселя найдем из векторной диаграммы:

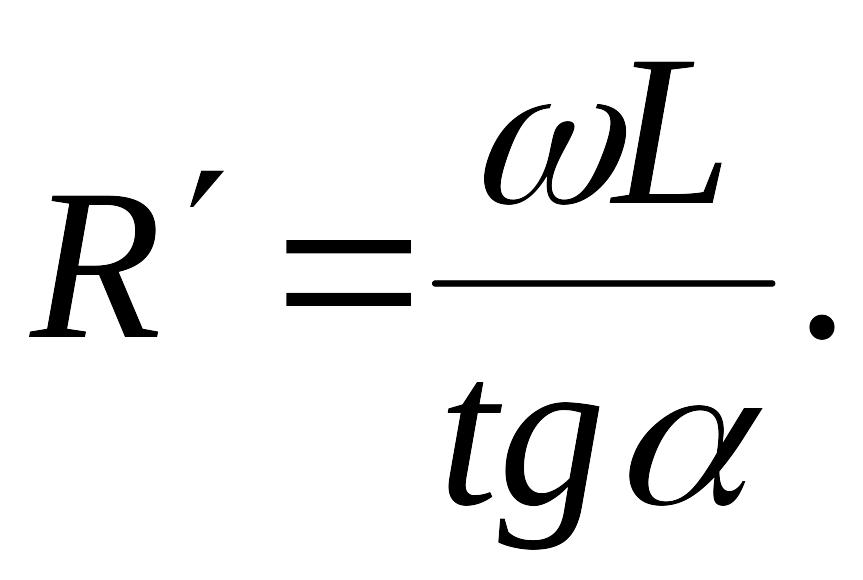
Мощность , выделяемая на конденсаторе, равна нулю, т.к. конденсатор не имеет активного сопротивления, поэтому сдвиг фаз между током и напряжением равен .

Мощность, выделяемая на сопротивлении :

Мощность, выделяемая на дросселе:

Мощность, выделяемая во всей цепи:

Коэффициент мощности для всей цепи: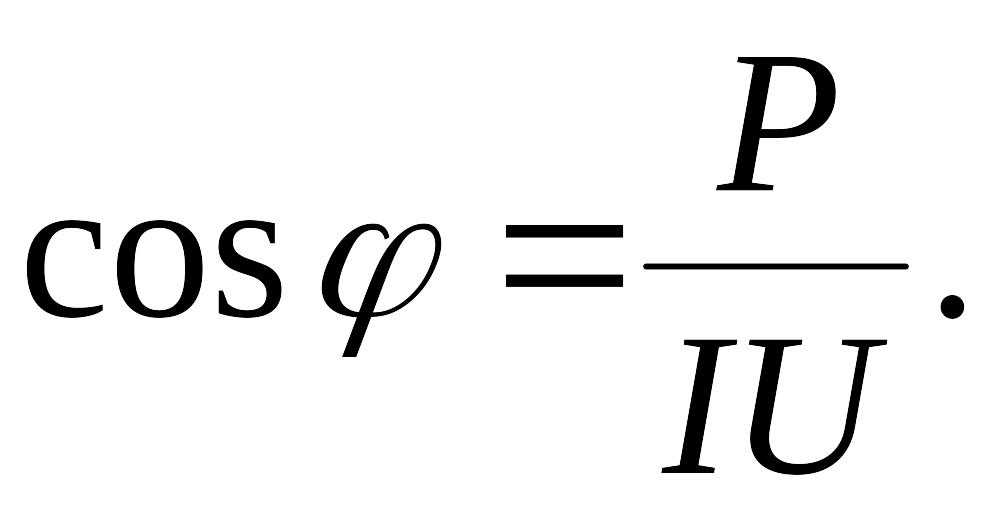

Выполним расчеты, получаем:

Ответ:

Домашнее задание:

[Л-2] – 14.16, 14.18, 14.20, 14.22, 14.25-14.28;

[Л-3] – 3.142, 3.143, 3.144, 3.146, 3.148, 3.150-3.155;

[Л-4] – 4.91, 4.94, 4.96, 4.100, 4.103, 4.108, 4.112.