III. Модуль 3. Электромагнитные колебания и волны

3.1. Занятие 7. Переменный электрический ток

Краткие теоретические сведения

Основные формулы

Переменным током называют ток, модуль и направление которого изменяются во времени.

Значение тока в любой момент времени называют мгновенным током .

Токи, мгновенные значения которых повторяются через равные промежутки времени в той же самой последовательности, называют периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом .

Для периодического тока:

Величина, обратная периоду, называется частотой 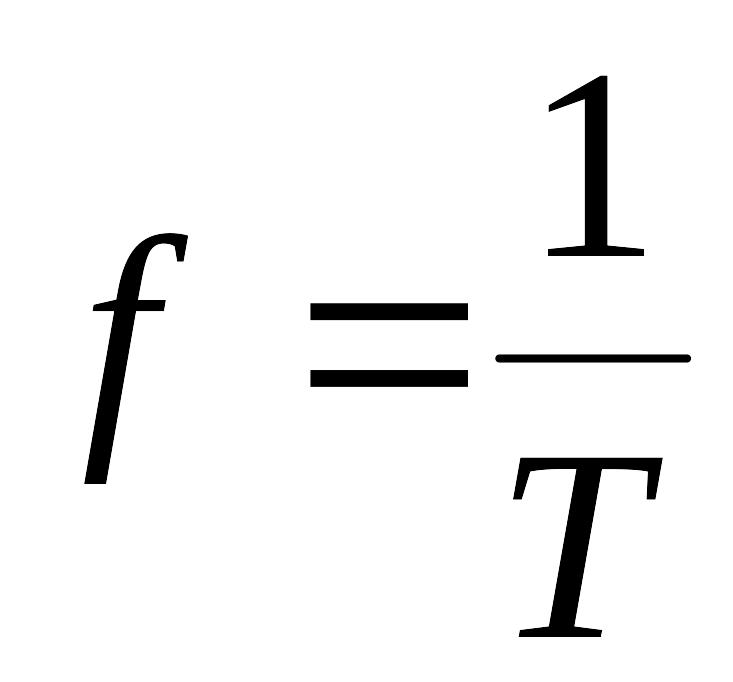. Частота измеряется в герцах. Угловая частота .

Синусоидальные токи являются синусоидальными функциями времени, мгновенное значение этого тока определяется выражением:

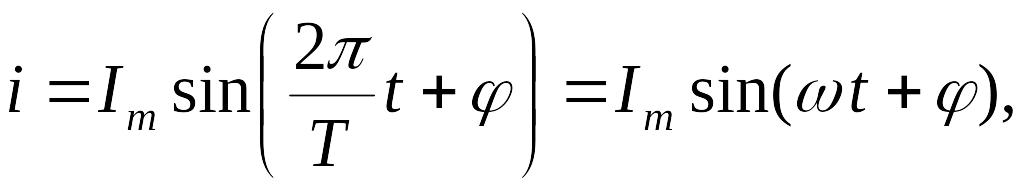
где - максимальное значение или амплитуда тока, аргумент синуса называется фазой. Угол равен фазе в начальный момент времени , поэтому называется начальной фазой.

Действующие значения тока и напряжения для синусоидального тока соответственно равны:

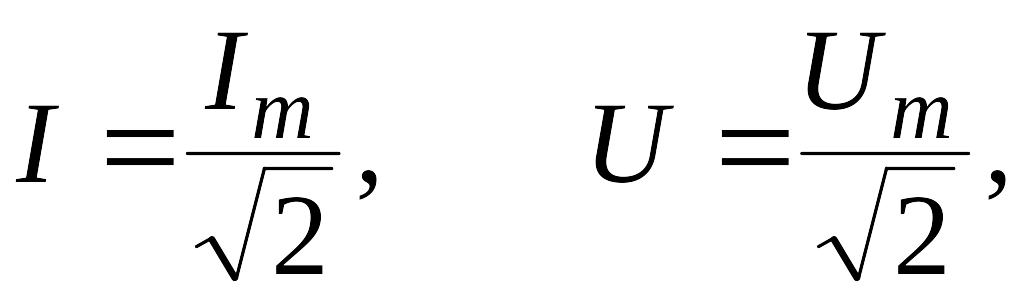
где - амплитуды тока и напряжения.

Ток и напряжения при последовательном соединении сопротивления, индуктивности и емкости:

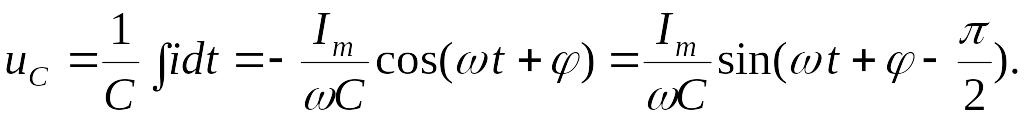
Постоянная интегрирования в выражении для принята равной нулю, так как в установившемся режиме напряжение на любом участке цепи синусоидально.

Из выражений для :

напряжение на сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает ток по фазе на угол , а напряжение на емкости отстает по фазе от тока на угол .

Метод векторных диаграмм заключается в том, что на графике изображаются амплитуды напряжений

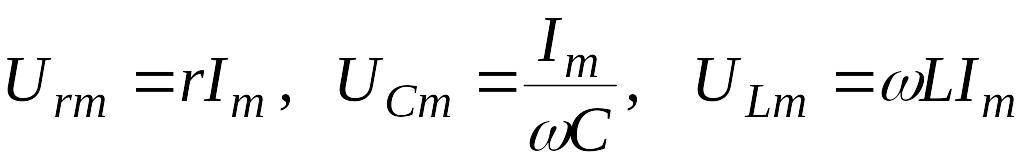
и их векторная сумма, равная вектору величины . На векторной диаграмме каждое напряжение изображается в виде вектора, модуль которого равен его амплитуде, а угол, который он составляет с осью тока, соответствует сдвигу фаз между этим напряжением и током.

Полное сопротивление цепи: 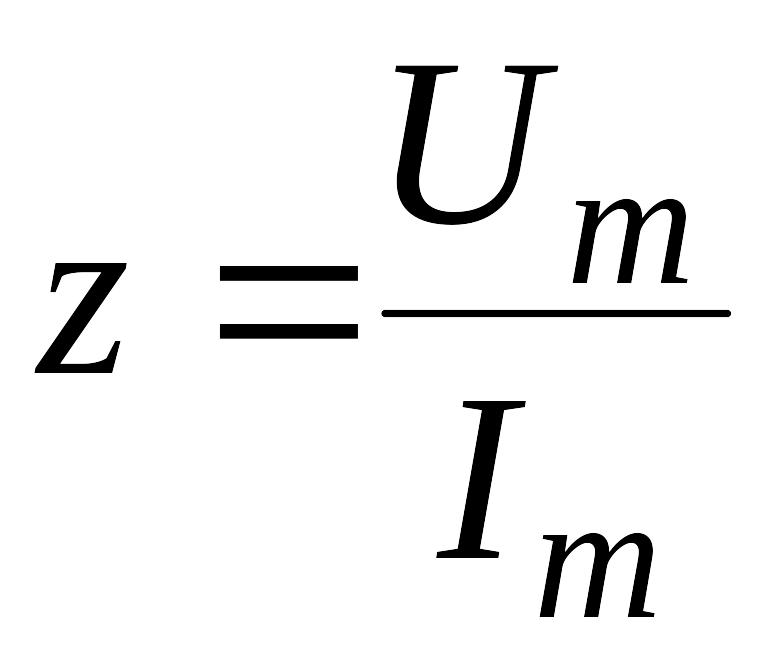- отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току, равно модулю комплексного сопротивления.

Реактивное сопротивление:

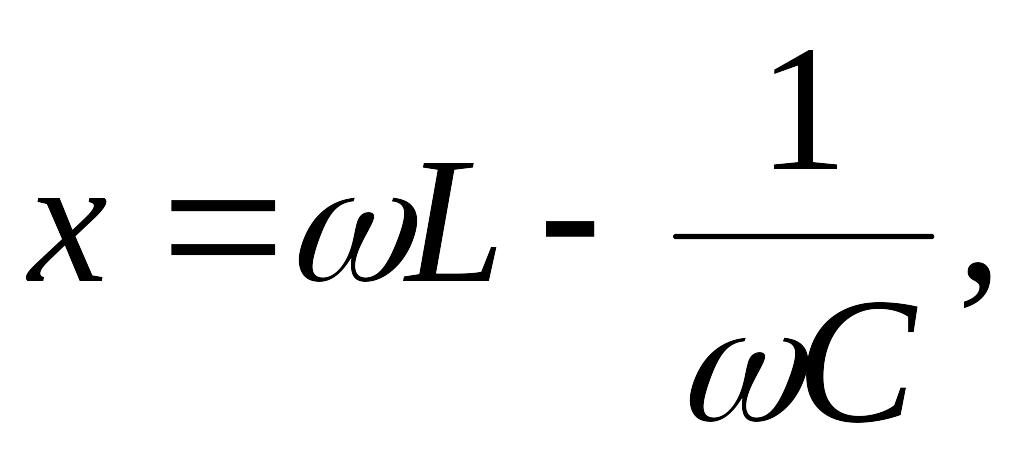
где индуктивное сопротивление:

емкостное сопротивление: .

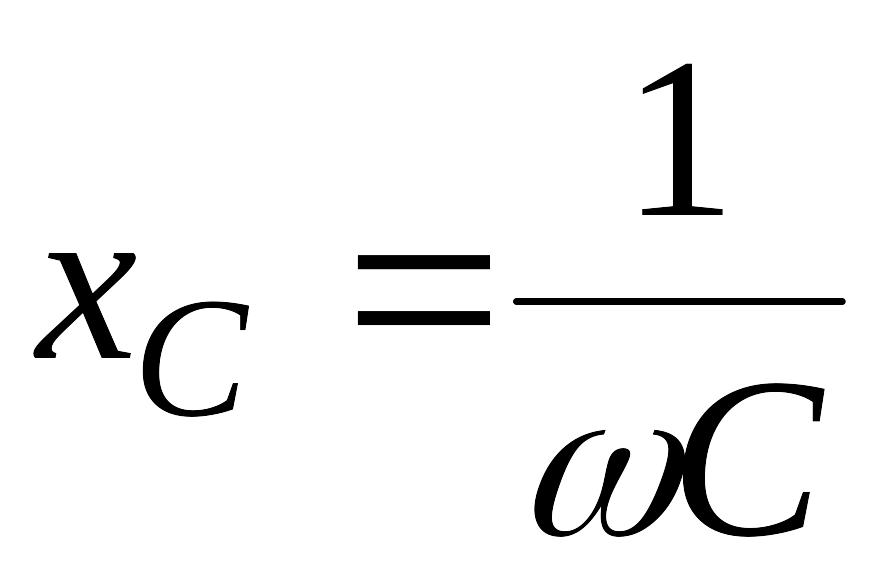Мгновенная мощность равна скорости совершения работы в данный момент времени:

Среднее значение мгновенной мощности за период называется активной мощностью. Активная мощность зависит от сдвига фаз между напряжением и током:

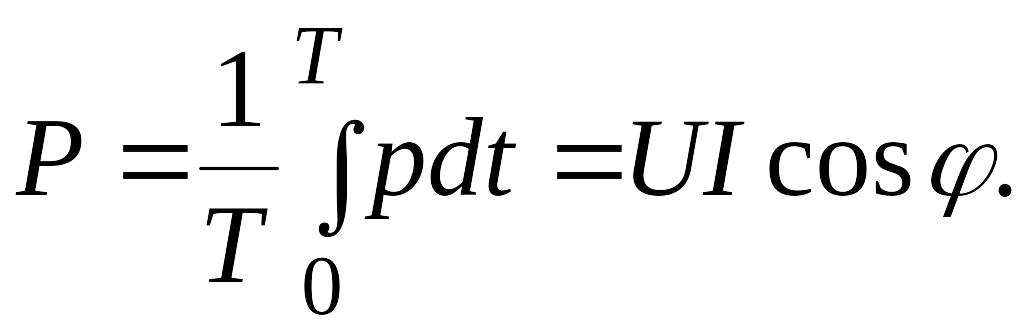
Полная мощность равна произведению действующих напряжения и тока:

.

Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:

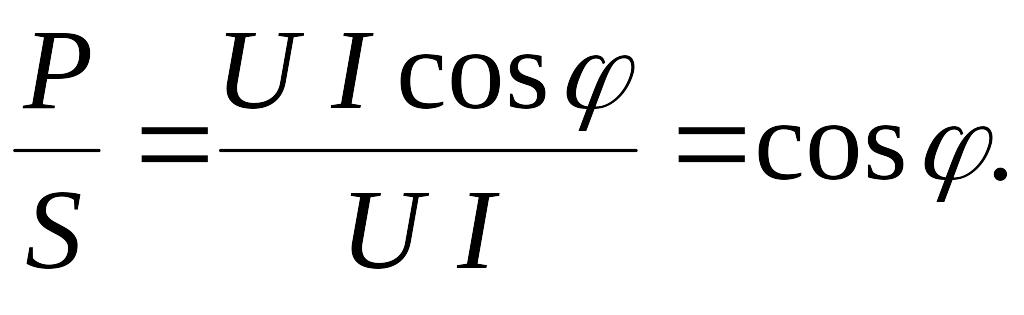
Реактивная мощность:

Активная, реактивная и полная мощности связаны соотношениями:

Резонансом называется такой режим цепи, содержащей катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением. При последовательном соединении сопротивления, индуктивности и емкости резонанс наступает при , значения противоположных по фазе напряжений на индуктивности и емкости равны, поэтому резонанс последовательной цепи называют резонансом напряжений.