8.7. Колебания связанных систем

До сих пор мы рассматривали колебания одного тела. Такие колебания описываются только одной переменной x, и поэтому их называют колебаниями с одной степенью свободы. На практике, однако, часто приходится иметь дело с колебаниями не одного, а нескольких связанных между собой тел. Для их описания требуется уже не одна, а несколько переменных (равное числу колеблющихся тел). Такие колебания называются колебаниями со многими степенями свободы.

В качестве примера таких колебаний рассмотрим колебание двух одинаковых математических маятников, связанных между собой невесомой пружиной (рис. 6.). При колебаниях такой системы будут изменяться две величины (поэтому эта колебательная система имеет две степени свободы) – смещения из положения равновесия маятников 1 и 2. Из-за деформации пружины эти смещения не будут равны друг другу. Будем считать эти колебания малыми. Тогда вертикальными смещениями маятников можно пренебречь и рассматривать их движения вдоль одной горизонтальной прямой. Положение колеблющихся тел 1 и 2 будем характеризовать смещениями x₁ и x₂ от своих положений равновесия О₁ и О₂ соответственно.

При отсутствии пружины на каждое тело будет действовать возвращающая сила которая вызывает гармонические колебания с собственной частотой При наличии пружины в дополнение к возвращающей силе появляется еще действующая сила от пружины, которая стремится «стянуть» маятники. Для тела 1 эта дополнительная сила зависит от превышения отклонения x₁ над отклонением x₂ и пропорциональна их разности: где k – жесткость пружины, дополнительная сила, действующая на второе тело, соответственно С учетом этого уравнения движения тел 1 и 2 запишутся в виде

(5.18)

Решение этой системы дифференциальных уравнений можно искать в виде Подставляя эти функции в уравнения системы (5.18), преобразуем ее в алгебраическую систему уравнений

(5.19)

Эта система будет иметь решение, если будет равен нулю определитель, составленный из коэффициентов при неизвестных A₁ и A₂, т.е. при условии, что Из этого равенства получаем Откуда находим два значения частоты ω: Таким образом, система с двумя степенями свободы обладает двумя собственными частотами. С увеличением числа степеней свободы системы будет увеличиваться и число возможных частот колебаний. Их совокупность образует частотный спектр системы.

Подставив значение в алгебраическую систему уравнений (5.19), получим, что а значит, и Этот случай соответствует симметричным колебаниям системы, когда оба маятника движутся в одну сторону. Подставляя в указанную систему второе значение частоты получим или Этот случай соответствует антисимметричным колебаниям системы, когда маятники смещаются в противоположные стороны. Симметричные колебания возникают если маятники одновременно отклонить на один и тот же угол в одну сторону и отпустить, а антисимметричные – при отклонении маятников на одинаковый угол, но в противоположные стороны. При симметричных колебаниях маятники колеблются в одинаковой фазе (совершают синфазные или синхронные колебания) с одинаковыми амплитудами и частотой ω₁, равной собственной частоте колебаний маятников. Пружина при этом будет оставаться в недеформированном состоянии, не оказывая никакого влияния на движение маятников. При антисимметричных колебаниях маятники совершают зеркально-симметричные противофазные (антифазные) колебания с частотой ω₂. В этом случае деформированная пружина будет стремиться повернуть маятники в ту же сторону, что и сила тяжести. Указанные два простейших движения, при которых каждый маятник совершает гармонические колебания, называют их нормальными колебаниями, или нормальными модами, а частоты ω₁ и ω₂ – нормальными частотами первой и второй соответственно.

Произвольные колебания двух связанных маятников может быть представлено в виде суперпозиции двух нормальных колебаний с частотами ω₁ и ω₂: Здесь A₁ и A₂ – амплитуды нормальных колебаний, значения которых определяются из начальных условий: 1) x₁(0) = x₂(0) = x₀ (в этом случае ; 2) x₁(0) = x₀, x₂(0) = = (в этом случае

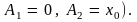
Отклоним теперь один маятник на величину удерживая другой маятник в положении равновесия, а затем отпустим оба маятника. Теперь x₁(0) = x₀, а x₂(0) = 0, поэтому A₁ + A₂ = x₀, откуда A₁ = A₂ = Движение маятников в этом случае будет происходить по законам

Это движение представляет собой произведение двух гармонических колебаний частотами и Если нормальные частоты близки друг к другу (что будет иметь место, когда связывающая маятники пружина будет слабая и ее влияние на маятники мало), то движение маятников будет представлять собой биения, показанные на рис. 5. Как видно из графиков колебаний маятников, их фазы отличаются на В начальный момент времени вся энергия колебаний сосредоточена у первого маятника. Но постепенно амплитуда его колебаний убывает, а амплитуда второго маятника возрастает и через промежуток времени т.е. через половину периода биений - частота биений), вся энергия будет сосредоточена у второго маятника. Затем энергия колебаний снова переходит к первому маятнику и т.д. – благодаря связывающей маятники упругой пружине происходит процесс перекачки энергии от одного маятника к другому.

Из-за рассеяния энергии колебания маятников будут затухающими. Для получения незатухающих колебаний необходимо наличие внешней гармонической силы. При вынуждающем действии ее на один из маятников оба маятника будут совершать колебания с частотой ω этой силы.

Для маятников с различными собственными частотами будет наблюдаться так называемый двугорбый резонанс. Зависимость отклонения маятников от частоты вынуждающей силы будет иметь вид, показанный на рис. 5., где ω₀₁ и ω₀₂ – собственные частоты первого и второго маятников соответственно. При первом резонансе маятники будут иметь одинаковые фазы колебаний, при втором – фазы колебаний будут противоположны.