8.5. Затухающие колебания

Рассмотренные выше колебания называются собственными колебаниями, так как они происходили при отсутствии внешних сил и трения; частота таких колебаний зависит только от свойств колеблющейся системы. Однако во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к убыванию энергии системы. А поскольку энергия пропорциональна квадрату амплитуды, то и к убыванию амплитуды. Поэтому если убыль энергии не восполняется, колебания будут затухать и через какое-то время прекратятся совсем.

При малых скоростях сила сопротивления пропорциональна скорости: где - коэффициент сопротивления. Уравнение движения частицы в этом случае будет иметь вид 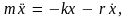или

(5.15)

где величина обозначенная здесь через есть циклическая частота гармонических колебаний в отсутствие затухания, т.е. собственная частота колеблющейся частицы, 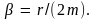. Постоянная , как мы увидим ниже, определяет время затухания колебаний, и поэтому ее называют коэффициентом затухания. Подстановкой уравнение (5.15) приводится к виду

(5.16)

Решение этого уравнения зависит от соотношения между и Если т.е. если то уравнение (5.11) не дает периодических решений. При таком условии колебания не возникают – частица апериодически приближается к положению равновесия. Это будет иметь место, если коэффициенте сопротивления Если же то, обозначив положительную разность через уравнение (5.16) перепишем в виде Это уравнение будет описывать гармонические колебания величины с частотой С учетом этого и введенной выше подстановки получаем

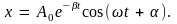(5.17)

Постоянные 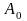и могут быть определены с помощью начальных условий.

Функция определяемая формулой (5.17), не является периодической, но величина x через равные промежутки времени проходит через нуль и достигает максимума и минимума (рис. 5.10). В этом смысле движение, описываемое формулой (5.17) является колебательным движением. Эти колебания называются затухающими колебаниями; величину называют частотой затухающих колебаний, а – их периодом. Множитель, стоящий перед осциллирующей функцией в (5.17), т.е. величину называют амплитудой затухающих колебаний. Как видим, амплитуда затухающих колебаний уменьшается по экспоненциальному закону и тем быстрее, чем больше коэффициент затухания. График изменения амплитуды показан пунктирной кривой на рис. 5.

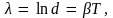Время по истечении которого амплитуда уменьшится в е ≈ 2,72 раза, называется временем затухания. Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, т.е. величину называют декрементом затухания. Логарифм этого отношения, т.е. величину называют логарифмическим декрементом затухания. Подставляя в формулу для соотношение получим 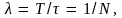где – число колебаний, совершающих затухающим

осциллятором за время затухания. Следовательно, Откуда видно, что чем меньше логарифмический декремент затухания (а он тем меньше, чем меньше коэффициент затухания), тем больше колебаний совершает осциллятор за время затухания.

Важной характеристикой осциллятора является величина Q, называемая добротностью. Она определяется как умноженное на 2π отношение энергии Е осциллятора в данный момент времени, к потере энергии за один период колебаний: Учитывая, что полная энергия пропорциональна квадрату амплитуды колебаний, будем иметь закон убывания полной энергии при затухающих колебаниях: где Е₀ – значение энергии в начальный момент времени t = 0. Отсюда находим убыль энергии за один период ( ):

Следовательно, добротность затухающего осциллятора она тем больше, чем меньше логарифмический декремент затухания. Добротность можно связать и с числом колебаний 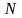за время затухания:

Как видим, добротность характеризует степень затухания колебаний при наличии сопротивления, а значит, и диссипацию энергии осциллятора во времени.

Поскольку у осциллятора с затуханием амплитуда колебаний с течением времени уменьшается, то его фазовая траектория не может

представлять собой замкнутую кривую. Вместо эллипса теперь получается скручивающаяся (по часовой стрелке) спираль (рис. 5.13, а). Она заканчивается в одной точке, соответствующей покою в состоянии равновесия. Эта точка, называемая центром, или аттрактором, как бы притягивает к себе со временем все фазовые траектории и является обобщением понятия равновесия.

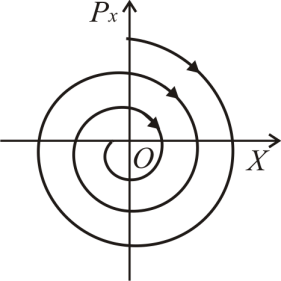
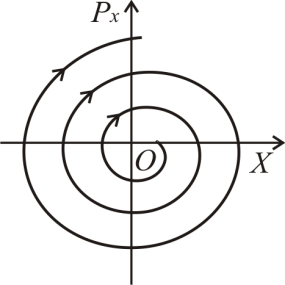
а) б)

Рис. 5.13

Если же энергия непрерывно поступает в колебательную систему из какого-либо источника, то система совершает колебания с нарастающей амплитудой и удаляется от состояния равновесия по раскручивающейся (по часовой стрелке) спирали (рис. 5.13, б). Подобные системы с так называемым отрицательным затуханием широко применяются для возбуждения, или генерации колебаний.