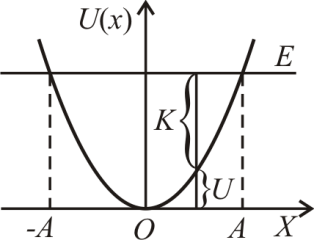- •Глава 8
- •8.1. Гармонические колебания
- •8.2. Маятники
- •1. Пружинный маятник
- •2. Математический маятник
- •3. Физический маятник
- •4. Крутильный маятник
- •8.3. Энергетические превращения при гармонических колебаниях
- •8.4. Сложение гармонических колебаний
- •8.4.1. Векторное и символическое представление
- •8.4.2. Сложение колебаний одного направления одинаковых частот.
- •8.4.3. Сложение колебаний одного направления разных частот.
- •8.4.4. Понятие о гармоническом анализе
- •8.5. Затухающие колебания
- •8.6. Вынужденные колебания. Резонанс
- •8.7. Колебания связанных систем
- •8.8. Автоколебания
- •8.9. Ангармонические колебания
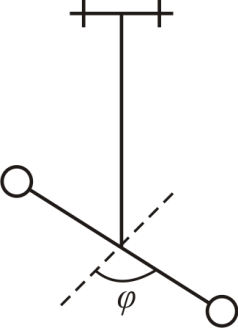
4. Крутильный маятник
Пример такого маятника показан на рис 5.6. Этот маятник представляет собой твердое тело, подвешенное на упругой нити
Рис. 8.6 |
или
стержне. Колебания крутильного маятника
происходят в горизонтальной плоскости
и обусловлены упругими силами, возникающими
в нити или стержне при закручивании.
Вращательный момент М,
с которым эти силы действуют на тело,
пропорционален углу поворота φ
тела из положения равновесия и направлен
против этого поворота:
 где
где
 – крутильная жесткость нити или стержня.
Основное уравнение динамики вращательного
движения твердого тела в этом случае
запишется в виде
– крутильная жесткость нити или стержня.
Основное уравнение динамики вращательного
движения твердого тела в этом случае
запишется в виде
 где I
– момент инерции тела относительно
вертикальной оси, проходящей через его
центр масс, или
где I
– момент инерции тела относительно
вертикальной оси, проходящей через его
центр масс, или

Это
уравнение гармонических колебаний
крутильного маятника. Частота колебаний
маятника
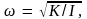 а
его период
а
его период

И в этом случае период колебаний определяется только параметрами маятника. Эта формула позволяет по известным крутильной жесткости K и периода колебаний Т определить момент инерции тела.
8.3. Энергетические превращения при гармонических колебаниях
Найдем энергию частицы, совершающей гармонические колебания. При колебательном движении частица обладает как потенциальной, так и кинетической энергией. Кинетическая энергия частицы с учетом (5.4) запишется в виде


где
 Потенциальная энергия частицы будет
определяться формулой
Потенциальная энергия частицы будет
определяться формулой С учетом того, что
С учетом того, что
 эту формулу запишем в виде
эту формулу запишем в виде
 Подставляя сюда x
по формуле (5.3), получим
Подставляя сюда x
по формуле (5.3), получим


Как видим, при
гармонических колебаниях происходит
периодическое изменение кинетической
и потенциальной энергии частиц, причем
частота колебаний энергии в два раза
больше, а период в два раза меньше частоты
и периода колебаний координаты частицы.
Заметим также, что поскольку средние
значения квадрата косинуса и синуса за
период одинаковы (и равны
 ),
то при гармонических колебаниях средние
значения кинетической и потенциальной
энергии одинаковы:
),
то при гармонических колебаниях средние
значения кинетической и потенциальной
энергии одинаковы:
 где угловые скобки обозначают усреднение
по времени. Полная энергия гармонических
колебаний частицы остается неизменной
с течением времени
где угловые скобки обозначают усреднение
по времени. Полная энергия гармонических
колебаний частицы остается неизменной
с течением времени

Из
этого равенства следует, что амплитуда
гармонических колебаний осциллятора
определяется его полной энергией:
 Видно также, что
Видно также, что

На рис. 5.7 показан
профиль потенциальной энергии
 гармонически колеблющейся частицы и
уровень ее полной энергии Е.
Границы движения частицы определим из
равенства
гармонически колеблющейся частицы и
уровень ее полной энергии Е.
Границы движения частицы определим из
равенства
 откуда
откуда
 Эти точки являются точками поворота.
На рисунке видно, что при движе-
Эти точки являются точками поворота.
На рисунке видно, что при движе-
Рис. 8.7 |
нии частицы справа налево от точки x = A к точке О ее потенциальная энергия уменьшается, а кинетическая возрастает. В положении равновесия О потенциальная энергия обращается в нуль, а кинетическая достигает максимального значения, равного полной энергии Е. На этом участке потенциальная энергия переходит в кинетическую. При дальнейшем движении от точки О к точке x = –A кинетическая энергия убывает, а потенциальная – увеличивается. На этом участке кинетическая энергия переходит в потенциальную. В точке –A кинетическая энергия обращается в нуль, а потенциальная достигает максимального значения, равного Е. При движении частицы слева направо на участке от точки –A до точки О потенциальная энергия частицы переходит в кинетическую, а на участке от точки равновесия О до точки A – кинетическая энергия переходит в потенциальную. Таким образом, дважды за один период колебания частицы ее потенциальная энергия перешла в кинетическую и кинетическая в потенциальную.
Состояние
колеблющейся частицы определяется ее
координатой
 и соответствующей проекцией импульса
и соответствующей проекцией импульса
 Фаза определяет состояние колеблющейся
частицы1.
Поскольку при гармонических колебаниях
Фаза определяет состояние колеблющейся
частицы1.
Поскольку при гармонических колебаниях

то разделим обе части первого равенства на Е, получим

В
координатах
 и
и
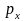 это есть уравнение эллипса с полуосями
это есть уравнение эллипса с полуосями
 и
и
 Следовательно, все состояния колеблющейся
частицы лежат на этом эллипсе. Плоскость
Следовательно, все состояния колеблющейся
частицы лежат на этом эллипсе. Плоскость

Рис. 8.8 |
 называют фазовой траекторией. При
колебаниях частицы ее координата
и проекция импульса
изменяются с течением времени
(изменяются состояния частицы).
Изображающая точка при этом движется
по фазовой траектории по часовой стрелке
и за время одного периода колебаний
частицы совершает полный оборот по
эллипсу. Следует отметить, что все
фазовые траектории, соответствующие
периодическому движению, являются
замкнутыми. Каждому значению энергии
соответствует свой эллипс. Поскольку
полуоси эллипса пропорциональны
называют фазовой траекторией. При
колебаниях частицы ее координата
и проекция импульса
изменяются с течением времени
(изменяются состояния частицы).
Изображающая точка при этом движется
по фазовой траектории по часовой стрелке
и за время одного периода колебаний
частицы совершает полный оборот по
эллипсу. Следует отметить, что все
фазовые траектории, соответствующие
периодическому движению, являются
замкнутыми. Каждому значению энергии
соответствует свой эллипс. Поскольку
полуоси эллипса пропорциональны
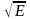 ,
то большей энергии соответствует больший
эллипс(рис. 5.8). Таким образом, гармонический
осциллятор описывается на фазовой
плоскости семейством подобных эллипсов
с общим центром в начале координат (рис.
5.8). Начало координат (x
= 0, px
= 0) представляет собой особую,
или сингулярную точку; ей, очевидно,
соответствует состояние устойчивого
равновесия колеблющейся частицы. В
окрестности этой точки все фазовые
траектории замкнуты. Изображающая
точка, находящаяся в исходный момент в
начале координат, там и остается, если
какие-либо случайные отклонения и толчки
не выведут из этой точки.
,
то большей энергии соответствует больший
эллипс(рис. 5.8). Таким образом, гармонический
осциллятор описывается на фазовой
плоскости семейством подобных эллипсов
с общим центром в начале координат (рис.
5.8). Начало координат (x
= 0, px
= 0) представляет собой особую,
или сингулярную точку; ей, очевидно,
соответствует состояние устойчивого
равновесия колеблющейся частицы. В
окрестности этой точки все фазовые
траектории замкнуты. Изображающая
точка, находящаяся в исходный момент в
начале координат, там и остается, если
какие-либо случайные отклонения и толчки
не выведут из этой точки.