8.2. Маятники

Маятниками называют механические системы и устройства, могущие совершать колебания вблизи положения устойчивого равновесия. Такими системами являются, например, пружинный маятник, математический маятник, физический маятник, крутильный маятник. Эти маятники показаны на рис. 5.2. При малых смещениях от положения равновесия маятники могут совершать колебания, которые можно рассматривать как гармонические, а сами маятники как гармонические осцилляторы. Рассмотрим колебания таких осцилляторов.

1. Пружинный маятник

Пружинный маятник представляет собой груз, подвешенный на пружине. На груз массой m (рис. 5.3) действуют две силы:

Рис. 8.2

направленная вниз сила тяжести mg и направленная вверх упругая сила пружины где - жесткость пружины. При некотором растяжении пружины эти силы уравновешивают друг друга: Направим ось X вертикально вниз и выберем начало отсчета в положении равновесия грузика. При смещении x груза из положения равновесия полное удлинение пружины станет равным а упругая сила Результирующая сила, действующая на груз c учетом того, что , будет равна

Уравнение движения груза будет иметь вид или

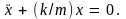
Сравнивая это с уравнением (5.1), находим частоту колебаний пружинного маятника и его период

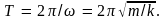
Как видим, эти параметры колебания определяются только величинами, характеризующие сам маятник.

2. Математический маятник

Математический маятник представляет собой небольшое (точечное) тело, подвешенное в поле тяжести Земли на невесомой

нерастяжимой нити (или невесомом стержне), длина которой l много больше размеров тела. Такое тело можно рассматривать как материальную точку. Отклоним маятник от положения равновесия на некоторый угол φ (рис. 5.4) и определим действующую при этом на маятник силу. Общая сила, действующая на маятник, равна силе тяжести mg, где m – масса маятника. Разложим эту силу на составляющую вдоль нити и на составляющую, перпендикулярную ей. Первая составляющая уравновешивается силой натяжения нити Т, а вторая вызывает движение маятника к положению равновесия

Рис. 8.4

(при φ = 0), т.е. является возвращающей силой. Эта составляющая, как видно из рисунка, равна (знак минус учитывает тот факт, что эта сила стремится уменьшить величину угла φ). В случае малых колебаний угол φ все время остается малым, и поэтому дугу окружности, по которой движется тело, можно считать прямой. Обозначим отклонение тела от положения равновесия через x; тогда при малых углах φ можно приближенно считать где l – длина маятника. Для возвращающей силы при малых φ будем иметь Уравнение движения маятника или Откуда получаем частоту колебания математического маятника и его период

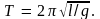
Как видим, период колебаний математического маятника определяется только длиной маятника и ускорением силы тяжести в месте его расположения.

3. Физический маятник

Этот маятник показан на рис. 5.5. Он представляет собой твердое тело, могущее вращаться вокруг горизонтальной оси под влиянием силы тяжести. При отклонении маятника на угол φ от вертикального положения на него относительно оси вращения будет действовать момент сил тяжести где m – масса тела, а – расстояние от центра масс С тела до оси враще-

Рис. 8.5

ния (она проходит через точку О) перпендикулярно плоскости рисунка), – расстояние от линии действия силы тяжести mg до оси вращения (плечо силы mg); знак минус выражает тот факт, что момент М стремится уменьшить угол φ. При малых колебаниях угол φ мал, так что Запишем основное уравнение динамики вращательного движения тела или где I – момент инерции тела относительно оси вращения. Это уравнение описывает гармонические колебания угла

отклонения маятника от вертикального положения, поэтому частота колебаний маятника , а его период

Сравнив эти выражения с формулами для частоты и периода колебаний математического маятника, мы видим, что свойства движения физического маятника совпадают со свойствами движения математического маятника с длиной 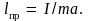Ее называют приведенной длиной физического маятника. Математический маятник является частным случаем физического маятника. Если считать, что вся масса физического маятника сосредоточена в центре масс, то его момент инерции Тогда а период

Тем самым мы пришли к формуле периода колебаний математического маятника.