8.4.4. Понятие о гармоническом анализе

Амплитудно-модулированное колебание (5.9) может быть представлено в виде совокупности трех строго гармонических колебаний с частотами Действительно, раскрыв скобки и воспользовавшись тригонометрической формулой произведения косинусов, будем иметь

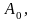
Мы получили три гармонических колебания с основной или несущей частотой и двумя боковыми частотами – нижней и верхней и амплитудами и соответственно.

Этот пример и пример с биениями показывают, что гармонические колебания не только можно складывать и получать при этом сложное негармоническое (но периодическое) колебание, но и что сложное периодическое колебание можно представить в виде совокупности гармонических колебаний различных частот.

Метод разложения сложных периодических колебаний на гармонические составляющие называют гармоническим или спектральным анализом, а саму совокупность гармонических составляющих сложного колебания – спектром этого колебания. Совокупность частот гармонических составляющих сложного негармонического колебания называется частотным спектром этого колебания. Частотный спектр представляют графически, откладывая по оси абсцисс частоты гармонических составляющих, а по оси ординат – их амплитуды. Частотный спектр рассмотренного негармонического колебания (5.9) показан на рис. 5.7, а, а частотный спектр биений – на рис. 5.7, б. Заметим, что в примере с амплитудной модуляцией основной вклад в результирующее колебание вносит гармоническая составляющая с частотой. (она имеет наибольшую амплитуду).

В общем случае задача о сложных негармонических колебаниях решается с помощью математической теоремы Фурье, согласно которой любая периодическая функция с периодом T может быть представлена в виде конечного или бесконечного числа гармонических функций, частоты которых являются целыми кратными частоте исходной функции. Применительно к данной физической задаче это означает, что любое периодическое негармоническое колебание с периодом T и частотой может быть представлено совокупностью конечного или бесконечного числа гармонических колебаний, частоты которых являются целыми кратными частоте где m – целое число. Математически в комплексной форме это можно выразить формулой

где f(t) – функция, описывающая сложное периодическое колебание с периодом T. Коэффициенты ряда при этом определяются формулой

Отдельные гармонические составляющие (члены ряда) с частотами ω, 2ω, 3ω и т.д. называют первой (или основной), второй, третей и т.д. гармониками. Коэффициенты A_m представляют собой комплексные амплитуды гармонических составляющих.

Гармонический анализ широко применяется при исследовании различных реальных колебаний.

8.4.5. Сложение взаимно перпендикулярных колебаний

Как видно из рис. 5.11, при равномерном движении точки М по окружности радиуса А с угловой скоростью ω ее проекции на взаимно перпендикулярные оси X и Y совершают гармонические колебания с одинаковой частотой и амплитудой А:

(5.10)

где предполагается, что Эти колебания отличаются по фазе на Следовательно, периодическое движение точки по окружности можно разложить на два взаимно перпендикулярных колебания с одинаковыми амплитудами и частотами, но отличающихся по фазе на Справедливо и обратное утверждение: если материальная точка одновременно совершает два

Рис. 8.11

взаимно перпендикулярных колебания одинаковой частоты и амплитуды и с раз- ностью фаз то результирую- щее движение точки будет происходить по окружности радиусом, равным амплитуде колебаний А и угловой скоростью, равной частоте колебаний . В самом деле, воз- водя выше записанные равенства в квадрат и складывая получим уравнение окруж- ности радиуса А:

В рассмотренном случае движение точки по окружности происходит против часовой стрелки (легко видеть, что в момент времени t = 0 v_x = 0, а – скорость направлена в положительном направлении оси Y против часовой стрелки). Если колебания по оси Y будут опережать по фазе колебания по оси X на т.е. если колебание точки по оси будут происходить по закону

(8.11)

то результирующее движение точки будет происходить по окружности радиуса А по часовой стрелке (при t = 0, v_x = 0, а – скорость направлена вдоль отрицательного направления оси Y).

Колебания, описываемые формулами (5.10) и (5.11), называются колебаниями, поляризованными по кругу или циркулярно-поляризованными колебаниями.

В случае, когда складываемые взаимно перпендикулярные колебания имеют разные амплитуды А и В, а сдвиг фаз т.е. если эти колебания происходят по закону

(8.12)

то выразив и , возведя полученные равенства в квадрат и сложив их, получим уравнение эллипса

В этом случае результирующее движение точки будет происходить по эллипсу, приведенному к осям координат, и с полуосями, равными амплитудам A и B против часовой стрелки при или по часовой стрелке при

Рис. 5.12

Наконец, если сдвиг фаз складываемых колебаний будет равен 0 или π, т.е. если колебания происходят по закону x = Acosωt, y = = Bcosωt или по закону x = Acosωt, y = Bcos(ωt ± π) = то результирующее движение точки будет гармоническим колебанием s(t), происходящем по прямой при или по прямой при Колебания такого типа называются линейно-поляризованными. Амплитуда такого колебания будет равна а частота – частоте складываемых колебаний ω. Это следует из равенства

Все рассмотренные случаи показаны на рис. 5.10. Они являются следствием общего уравнения

(5.13)

которое получается из закона колебаний точки вдоль взаимно перпендикулярных направлений X и Y:

(5.14)

если из этих равенств исключить время t. Уравнение (5.13) есть уравнение эллипса, размеры и ориентация которого относительно осей X и Y определяется параметрами А и В и разностью фаз δ складываемых колебаний. При этом, поскольку 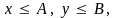то и он, как и все фигуры, изображенные на рис. 5.10, оказывается вписанным в прямоугольник со сторонами 2А и 2В. В рассмотренных выше соотношениях между указанными параметрами А и В и значением разности фаз δ этот эллипс вырождается в окружность, прямую и приводится к осям координат.

Колебания, описываемые формулами (5.12) или в общем случае формулами (5.14) называются эллиптически поляризованными.

Материальная точка, которая может совершать колебания в двух взаимно перпендикулярных направлениях, называется двумерным осциллятором. Соотношения (5.14) выражают собой закон движения двумерного гармонического осциллятора.

Если частоты складываемых взаимно перпендикулярных колебаний не одинаковы, но кратны друг другу, то получаются кривые, называемые фигурами Лиссажу. Рассмотренные выше случаи являются частными случаями фигур Лиссажу, когда частоты 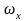и равны друг другу.