Глава 8

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

8.1. Гармонические колебания

Рассмотрим движение частицы выведенной из положения устойчивого равновесия вдоль оси X. На частицу будет действовать возвращающая сила где x – смещение частицы из положения равновесия. Совместим положение равновесия с началом О координатной оси X. Тогда x будет являться x–координатой частицы. Уравнение движение частицы будет иметь вид

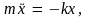
или

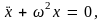(8.1)

где 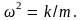С учетом этого обозначения возвращающую квазиупругую силу можно записать в виде

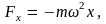
К уравнению (8.1) можно прийти и исходя из уравнения Лагранжа (5.16). Лагранжиан колеблющейся частицы

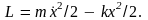
Подставляя его в уравнение (5.16), придем к уравнению движения, а затем и к уравнению (8.1).

В соответствии с (5.1) вторая производная координаты x пропорциональна самой координате x со знаком минус: 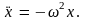Такому условию, как легко убедиться, удовлетворяют тригонометрические функци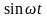и и 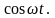Поэтому общее решение уравнения (5.1) следует искать в виде

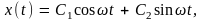(5.2)

где C₁ и C₂ – постоянные. Введя новые произвольные постоянные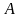 и 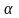, такие что

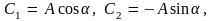
решение (5.2) запишем в так называемом стандартном виде

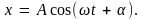(8.3)

Постоянные А и определяются по начальным значениям смещения и скорости, т.е. из начальных условий

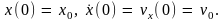
Движения, происходящие по закону косинуса (5.3) (или по закону синуса 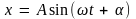), называют гармоническими колебаниями. Поскольку функция (8.3) бесконечна во времени то и гармонические колебания, формально описываемые функцией (5.3), являются бесконечными во времени. Частица, совершающая гармонические колебания, называется гармоническим осциллятором. Уравнение движения (5.1) называют уравнением движения гармонического осциллятора.

Таким образом, частица, выведенная из положения устойчивого равновесия и предоставленная самой себе, будет совершать гармонические колебания. При гармонических колебаниях частица через равные промежутки времени Т проходит через одни и те же положения (точки) и в одном и том же направлении. Указанный промежуток времени, т.е. величину Т, называют периодом гармонических колебаний. При квазиупругой силе, а значит, при параболической потенциальной энергии период колебаний определяется общей формулой (5.13),

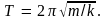
Так как период косинуса (и синуса) равен 2π, то значение x не изменится, если к времени t в (5.3) прибавить величину 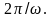Следовательно, период гармонических колебаний Т = Откуда находим: 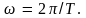Как видим, величина ω есть число колебаний, совершаемых за промежуток времени 2π. Эту величину называют круговой или циклической частотой колебаний. Вводят также линейную частоту или просто частоту колебаний ν, определяемую как число колебаний за единицу времени 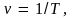величина ν измеряется в герцах (Гц, 1Гц = 1с^–1). С круговой частотой она связана соотношением

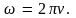
Поскольку максимальное значение косинуса равно единице, то параметр А в формуле гармонических колебаний (5.3) определяет

максимальное смещение частицы из положения равновесия и называется амплитудой колебаний. Величина x изменяется в пределах от – А до А, как показано на рис. 5.1.

Рис. 8.1

Аргумент косинуса, т.е. функция 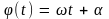называется фазой колебаний, – начальной фазой колебаний (в момент времени t = 0: 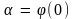). Часто величину называют просто фазой колебаний. Соответствующим выбором начала отсчета времени эту величину можно сделать, равной нулю.

Продифференцировав формулу колебаний (5.3) по времени, получим формулу колебаний скорости

(5.4)

а, продифференцировав скорость, получим формулу колебаний ускорения

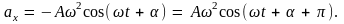
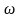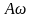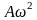Следовательно, при гармонических колебаниях скорость и ускорение также совершают гармонические колебания с той же частотой и амплитудами и соответственно. При этом колебания скорости опережают колебания смещения на 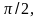а колебания ускорения – на 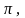а так как

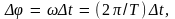
то

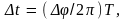
а значит, опережение по времени 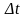составляет соответственно половину и четверть периода Т.