21.2 Інтерполяція та екстраполяція.

Інтерполяція функції y (x) однієї змінної х, заданої (n-1) вузлами y_i (x_i), де i=0, 1, 2, ..., n, заключається у находженні значень y по значенням х, що знаходяться в проміжках між вузлами x_i. При інтерполяції функція y (x) замінюється інтерполяційним поліномом P (x), значення якого P (x_i) у вузлах точно співпадають з y (x_i). Значення n задає степінь полінома P(x).

Формули Лагранжа для інтерполяції при рівномірному розташуванні вузлів забезпечують найменший час інтерполяції, не потребують відновлення вводу y_i та x₀ для обчислення кожного y(x) та дозволяють обчислювати y_i у вузлах x_i (наприклад, для контролю правильності обчислень). У цих формулах індексом 0 позначається центральний вузол. Для n+1=2÷6 формули Лагранжа мають вигляд

y(x)₂=(1-p)y₀+py₁+0,125h²y¹¹(ξ);

y(x)₃= y_-1+(1-p²)y₀+ y₁+0,065h³y¹¹¹(ξ);

y(x)₄= -

де

де

де

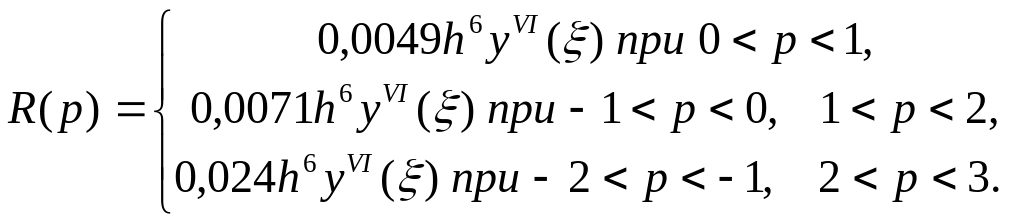
В цих формулах

x=x₀+px, p=(x-x₀)/h,

де h – крок розташування вузлів, індекс у y(x) відповідає числу вузлів (h+1), yⁿ⁺¹(ξ) – максимальне значення похідної y(x)для точки x= ξ, що лежить в межах інтерполяції. Останній член формули (він в програмах не обчислюється) характеризує погрішність інтерполяції.

Програма 2

10 PRINT ’ІНТЕРПОЛЯЦІЯ ПРИ H=CONST ЗА ФОРМУЛАМИ ЛАГРАНЖА’

20 INPUT ’ЗАДАЙТЕ СТЕПІНЬ ПОЛІНОМУ M=1-5 M=’M:LETN=M+1

30 INPUT ’ВВЕДІТЬ X0, H ’Z,H: IF N=3 THEN 100

40 IF N=4 THEN 140

50 IF N=5 THEN 190

60 IF N=6 THEN 250

70 INPUT ’ВВЕДІТЬ Y0, Y1 ’A, B

80 INPUT ’ВВЕДІТЬ X=’X:LETP=(X-Z)/H

90 LETY=(1-P)*A+P*B:PRINT’Y=’Y:GOTO 80

100 INPUT ’ВВЕДІТЬ Y-1, Y0, Y1 ’A, B, C

110 INPUT ’ВВЕДІТЬ X=’X:LETP=(X-Z)/H

120 LETY=P*(P-1)*A/2+(1-P*P)*B+P*(P+1)*C/2

130 PRINT ’Y=’Y:GOTO 110

140 INPUT ’ВВЕДІТЬ Y-1, Y0, Y1, Y2 ’A, B, C, D

150 INPUT ’ВВЕДІТЬ X=’X:LETP=(X-Z)/H:LETE=(P-2)/2

160 LETY= -P*(P-1)*E*A/3+(P*P-1)*E*B

170 LETY=Y-P*(P+1)*E*C+P*(P*P-1)*D/6

180 PRINT ’Y=’Y:GOTO 150

190 INPUT ’ВВЕДІТЬ Y-2, Y-1, Y0, Y1, Y2 ’A, B, C, D, E

200 INPUT ’ВВЕДІТЬ X=’X:LETP=(X-Z)/H

210 LETF=(P*P-1)/2:LETK=(P*P-4)/2

220 LETY=F*P*(P-2)*A/12-(P-1)*P*K*B/3+F*K*C

230 LETY=Y-(P+1)*P*K*D/3+F*P*(P+2)*E/12

240 PRINT ’Y=’Y:GOTO 200

250 INPUT ’ВВЕДІТЬ Y-2, Y-1, Y0, Y1, Y2, Y3 ’A, B, C, D, E, F

260 INPUT ’ВВЕДІТЬ X=’X:LETP=(X-Z)/H:LETM=P*P-1

270 LETI=M/24:LETJ= -P*I*(P-3):LETK=M-3:LETL=K*(P-3)/12

280 LETY=J*(P-2)*A/5+L*P*(P-1)*B/2-M*L*C

290 LETY=Y+P*(P+1)*L*D+J*(P+2)*E+P*I*K*F/5

300 PRINT ’Y=’Y:GOTO 260:END

Існують різні методи інтерполяції: лінійна, квадратна, кубічна.

Існує ряд спеціальних видів полінома P(x) (Ньютона, Еверетта та ін). Однак слід пам’ятати, що поліном P(x), що має P(x_i)=y(x_i), являється завжди єдиним.

Інтерполяція за методом Ейткена заключається в обчисленні y(x) при довільно розміщених вузлах без явного побудування інтерполяційного поліному. Останнє досягається шляхом послідовного застосування формул лінійної інтерполяції:

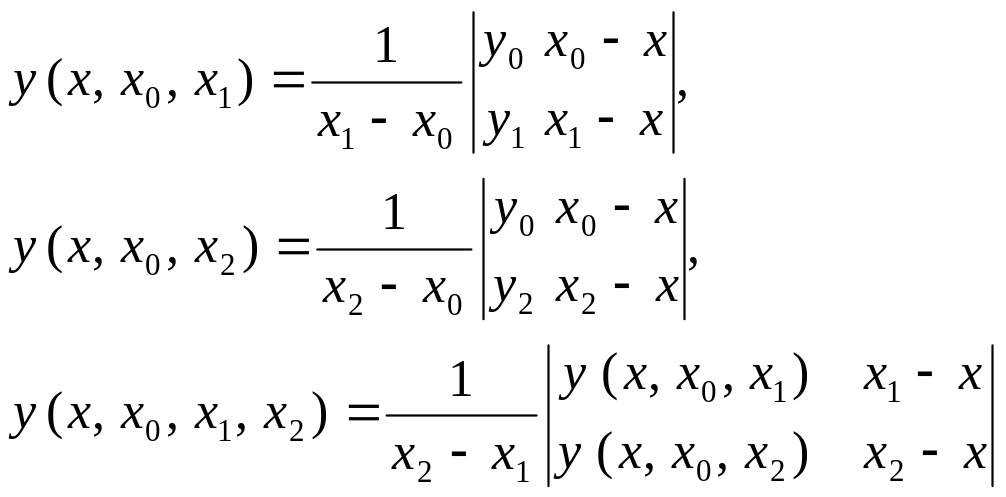
і т.д.

Програма 3

05 PRINT ’ІНТЕРПОЛЯЦІЯ ТАБЛИЦЬ З ЧИСЛОМ ВУЗЛІВ ДО ШЕСТИ’

10 INPUT ’ЧИСЛО ВУЗЛІВ ДО ШЕСТИ M=’M

20 LETB2=0:LETB3=0:LETB4=0:LETB5=0:LETB6=0:LETX3=0:LETX4=0:LETX5=0

30 INPUT ’ВВЕДІТЬ X0, Y0’ X0, Y0

40 INPUT ’ВВЕДІТЬ X1, Y1’ X1, Y1

50 LETB0=Y0:LETQ1=(Y1-Y0)/(X1-X0):LETB1=Q1

60 IF M=2 THEN 210

70 INPUT ’ВВЕДІТЬ X2, Y2’ X2, Y2

80 LETQ2=(Y1-Y0)/(X2-X0):LETR2=(Q2-Q1)/(X2-X1)

90 LETB2=R2: IF M=3 THEN 210

100 INPUT ’ВВЕДІТЬ X3, Y3’ X3, Y3

110 LETQ3=(Y3-Y0)/(X3-X0): LETR3=(Q3-Q1)/(X3-X1)

120 LETS3=(R3-R2)/(X3-X2):LETB3=S3: IF M=4 THEN 210

130 INPUT ’ВВЕДІТЬ X4, Y4’ X4, Y4

140 LETQ4=(Y4-Y0)/(X4-X0):LETR4=(Q4-Q1)/(X4-X1)

150 LETS4=(R4-R2)/(X4-X2):LETL4=(S4-S3)/(X4-X3)

160 LETB4=L4: IF M=5 THEN 210

170 INPUT ’ВВЕДІТЬ X5, Y5’ X5, Y5

180 LETQ5=(Y5-Y0)/(X5-X0):LETR5=(Q5-Q1)/(X5-X1)

190 LETS5=(R5-R2)/(X5-X2):LETL5=(S5-S3)/(X5-X3)

200 LETB5=(L5-L4)/(X5-X4)

210 INPUT ’ВВЕДІТЬ X=’X

220 PRINT ’Y=’((((B5*(X-X4)+B4)*(X-X3)+B3)*(X-X2)+B2)*(X-X1)+B1)*(X-X0)+B0

230 GOTO 210: END

Інтерполяція поліномом Лагранжа при довільному розміщенні вузлів в загальному випадку зводиться до обчислення y(x)=L_n(x) за допомогою інтерполяційного поліному, що має вигляд (рис.2)

Програма 4

10 PRINT ’ІНТЕРПОЛЯЦІЯ ПО ЛАГРАНЖУ ДЛЯ N+1 ВУЗЛІВ’

20 INPUT ’ВВЕДІТЬ N=’N:DIM A(N):DIM B(N)

30 FOR I=0 TO N:PRINT !3.0!’ВВЕДІТЬ X’ I

40 INPUT A(I):PRINT ’ВВЕДІТЬ Y’ I

50 INPUT B(I):NEXT I

60 INPUT ’ВВЕДІТЬ X=’X:LETS=0

70 IF X=A(0) THEN PRINT !F1.9!’Y(X)=’B(0):GOTO 60

80 FOR J=1 TO N:LETC=1:FOR I=1 TO N

90 LETD=A(J)-A(I):IF I=J THEN LETD=X-A(J)

100 IF D=0 THEN PRINT!1.9!’Y(X)=’B(I):GOTO 60

110 LETC=C*(X-A(I))/D:NEXT I

120 LETS=S+C*B(J):NEXT J

130 PRINT !1.9!’Y(’X’)=’S:GOTO 60:END

Програма 5

10 PRINT ’ПОБУДОВА ІНТЕРПОЛЯЦІЙНОГО ПОЛІНОМУ НЬЮТОНА’

20 PRINT ’ТА ІНТЕРПОЛЯЦІЯ ПРИ ДОВІЛЬНО РОЗТАШОВАНИХ ВУЗЛАХ’

30 INPUT ’ЗАДАЙТЕ ЧИСЛО ВУЗЛІВ N=’N:DIM A(N), F(N), X(N), Y(N)

40 FOR I=1 TO N:PRINT!2.0!’ X’ I’ , Y’ I

50 INPUT X(I),Y(I):NEXT I:LETA(1):LETF(N)=Y(1)

60 FOR I=1 TO N-1:LETF(I)=0:NEXT I

70 FOR K=1 TO N-1:FOR I=1 TO N-1

80 LETY(I)=(Y(I+1)-Y(I))/(X(I+K)-X(I)):NEXT I

90 LETR=1:IF K/2-INT(K/2)< >0 THEN LETR= -1

100 LETP=1:FOR J=1 TO K:LETP=P*X(J):NEXT J

110 LETA(K+1)=R*P:IF K=1 THEN 170

120 FOR L=1 TO K:LETW=0:FOR M=1 TO L

130 LETR=1:IF K/2-INT(K/2)< >0 THEN LETR= -1

140 LETS=0:FOR P=1 TO K:LETS=S+R*(1/X(P))^M:NEXT P

150 LETW=W+(-R)*A(K+1+M-L)*S:NEXT M

160 LETA(K-L+1)=W/L:NEXT L

170 FOR J=N TO N-K STEP -1

180 LETF(J)=F(J)+A(J-N+K+1)*Y(11):NEXT J:NEXT K

190 PRINT ’КОЕФІЦІЄНТИ СТЕПІННОГО МНОГОЧЛЕНУ’

200 FOR I=1 TO N:PRINT !2.0!’A’N-I !F1.9! ’=’ F(I):NEXT I

210 INPUT ’ ВВЕДІТЬ ЗНАЧЕННЯ X=X’X:LETS=F(1):FOR I=1 TO N-1

220 LETS=S*X+F(I+1):NEXT I

230 PRINT !F1.9! ’Y(X)=’S:GOTO 210:END

Екстраполяція – отримання значень y(x) при x, що не належить відрізку [x₀, x_n] або [x₁, x_n+1], також здійснюється за описаними вище програмами, але з суттєво більшою погрішністю. Для гладеньких y(x) екстраполяція доцільна при x, що виходять за вказані межі не більше ніж на h/2.

Зворотня інтерполяція – процес знаходження значень x за заданими значеннями y. Вона може виконуватися за будь-якою програмою інтерполяції з довільно розташованими вузлами. При цьому замість значень x_i вводяться значення y_i, а замість y_i – значення x_i.

Багатоінтервальна інтерполяція заключається в інтерполяції y_i(x_i) в ряді часткових інтервалів (обмежених двома вузлами або групою вузлів) окремими поліномами невисокого ступеня. Така інтерполяція може застосовуватися при широкому загальному відрізку [a, b], коли звичайна інтерполяція поліномом високого ступеня дає більшу погрішність і веде до більшого часу обчислень. Зауважимо також, що по виду полінома і значенням його коефіцієнтів важко судити про вид залежності y(x).

Багатоінтервальна кусочно-лінійна інтерполяція при рівномірному розташуванні вузлів зводиться до завдання початкового значення x₀=a, кроку h (відстань між вузлами), номеру n останнього вузла та (n+1) ординат y₀, y₁, ..., y_n, після чого обчислення y(x) при заданому x виконується за формулами

i=int((x-a)/h),

y(x)=y_i+(y_i+1-y_i)(x-ih-a)/h.

Завдання асимптотичної поведінки y(x) при x<x₀=ax>b=a+nh заключається в лінійній екстраполяції, тобто обчисленні y(x) за межами відрізку [a, b] за формулами

y(x)=y₀+(x-a)(y₁-y₀)/h при x<a,

y(x)=y_n+(x-b)(y_n-y_n-1)/h при x>b.

Таке завдання не завжди строго, але дозволяє уникнути грубих спотворень асимптотичної поведінки екстраполюючої функції y(x) за межами відрізку [a, b], які нерідко спостерігаються при звичайній поліноміальній екстраполяції.

Багатоінтервальна квадратична інтерполяція заключається в задаванні парного числа парних інтервалів (n – парне число) з обчисленням y(x)при заданому x за формулами (x₀=a) i=int((x-a)/2h)+1, p=(x-a-ih)

та

Вираження для y(x) є інтерполяційна формула Лагранжа для трьох ординат, що застосовується для кожного часткового інтервалу.

Асимптотична поведінка y(x) задається за допомогою лінійної екстраполяції з обчисленням першої похідної в кінцях загального відрізку [a, b] за формулами чисельного диференціювання для трьох точок:

y(x)=y₀+(x-a)(4y₁-y₂-3y₀)/2h при x≤a,

y(x)=y_n+(x-b)(3y_n+y_n-2-4y_n-1)/2h при x≥b.

Сплайн-інтерполяція є спеціальний вид багатоінтервальної інтерполяції, при якому поліном, що інтерполює, забезпечує не тільки рівність y(x) значенням y_i у вузлах, але й неперервність заданого числа перших похідних на кордонах часткових інтервалів. В загальному випадку сплайн задається глобальним способом, тобто з використанням усіх вузлів при будь-якому їхньому розташуванні.

Кубічний сплайн, заданий локально, - це інтерполююча функція у вигляді полінома третьої ступені, що обчислюється за формулами:

i=int ((x-a)/h),

де m_i та m_i+1 – перші похідні y(x). Похідні локального сплайну можуть задаватися двома способами.

Програма 6

10 PRINT ’АПРОКСИМАЦІЯ, ІНТЕРПОЛЯЦІЯ ТА ЕКСТРАПОЛЯЦІЯ’

20 PRINT ’СПЛАЙНАМИ ПРИ ЛОКАЛЬНОМУ ЇХНЬОМУ ЗАВДАННІ’

30 INPUT ’ВВЕДІТЬ ПОЧАТКОВЕ ЗНАЧЕННЯ X0=’A

40 INPUT ’ВВЕДІТЬ КРОК H=’H

50 INPUT ’ВВЕДІТЬ НОМЕР ОСТАННЬОГО ВУЗЛА N=’N:DIM Y(N)

60 FOR I=0 TO N:PRINT!3.0!’ВВЕДІТЬ Y’I

70 INPUT Y(I):NEXT I

80 INPUT ’ВВЕДІТЬ ПОРЯДОК 1, 2 АБО 3 ПОЛІНОМУ’P

90 IF P=2 THEN 130

100 IF P=3 THEN 150

110 INPUT ’ВВЕДІТЬ X=’X:GOSUB 1000

120 PRINT !F1.9!’Y(X)=’W:GOTO 110

130 INPUT ’ВВЕДІТЬ X=’X:GOSUB 2000

140 PRINT!F1.9!’Y(X)=’W:GOTO 130

150 PRINT ’ЗАДАЙТЕ КОД 0-DY/DX НЕ ЗАДАЄТЬСЯ:DIM M(N)

160 INPUT ’ЗАДАЙТЕ КОД 1-DY/DX ЗАДАЄТЬСЯ’K

170 IF K=0 THEN 200

180 FOR I=0 TO N:PRINT!3.0!’ВВЕДІТЬ DY/DX’I

190 INPUT M(I):NEXT I:GOTO 230

200 LETM(0)=(4*Y(1)-Y(2)-3*Y(0))/2/H

210 LETM(N)=(3*Y(N)+Y(N-2)-4*Y(N-1))/2/H

220 FOR I=1 TO N-1:LETM(I)=(Y(I+1)-Y(I-1))/2/H:NEXT I

230 INPUT ’ВВЕДІТЬ X=’X:GOSUB 3000