Тема 5.3. Оцінка результатів вимірювання. Розрахунок математичного сподівання і дисперсії.

Оцінка результатів вимірювання.

Щоб краще з'ясувати природу похибок і вивчити методи їх обліку і вилучення, розглянемо обидві групи похибок ізольовано, тобто, говорячи про випадкові похибки, будемо вважати, що систематичні похибки вилучено або враховано, і навпаки.

Якщо в процесі вимірювання встановлено, що випадкова складова похибки відсутня або зневажливо мала, результати вимірювання оцінюють в такій послідовності:

вивірянням знаходять основну похибку засобу вимірювання і варіацію показників, порівнюють їх з класом точності вивіряльного засобу вимірювання (або допустимою похибкою і допустимою варіацією);

в процесі вимірювання визначають додаткові похибки; порівнюють результувальну похибку (основна і додаткові) з допустимою результувальною похибкою і роблять висновок про придатність засобу вимірювання.

Якщо в процесі вимірювання встановлено помітні розход­ження в результатах окремих вимірювань, що носять індетермінований характер, потрібно вилучити систематичну по­хибку і після цього оцінювати результати вимірювання, залучаючи методи теорії ймовірності і математичної статистики. Математич­ний апарат теорії ймовірності і математичної статистики є дос­татнім для вивчення задачі випадкових похибок вимірювання і до­бре узгоджується з дослідними даними вимірювань.

В тих випадках, коли неможливо вилучити систематичні похибки або підрозділити похибку на систематичну і випадкову, результат вимірювання розглядають як випадкову величину.

Для оцінки результатів вимірювання, що містять випадкові похибки, користуються поняттями і методами теорії ймовірності і математичної статистики.

Розрахунок математичного сподівання і дисперсії.

Математичне сподівання М (х) випадкової величини (по­хибки) - це таке її значення, навколо якого групуються результати окремих вимірювань (похибок). Математичне сподівання випадкової величини визначається як сума добутків всіх можливих значень випадкової величини х_і, на ймовірність Р_і цих значень:

(24)

Для неперервних випадкових величин

(25)

Якщо спостерігається нормальний розподіл випадкових похибок, то математичне сподівання випадкової похибки дорівнює нулю (рис. 14, б). Чим крутішою є крива розподілу випадкових похибок, тим менше число похибок відрізняється від нуля. Що більш похилою є крива, то більшим є розсіяння (розкид) результатів спостережень відносно математичного сподівання, тобто тим меншою є ймовірність появі похибок, близьких до 0.

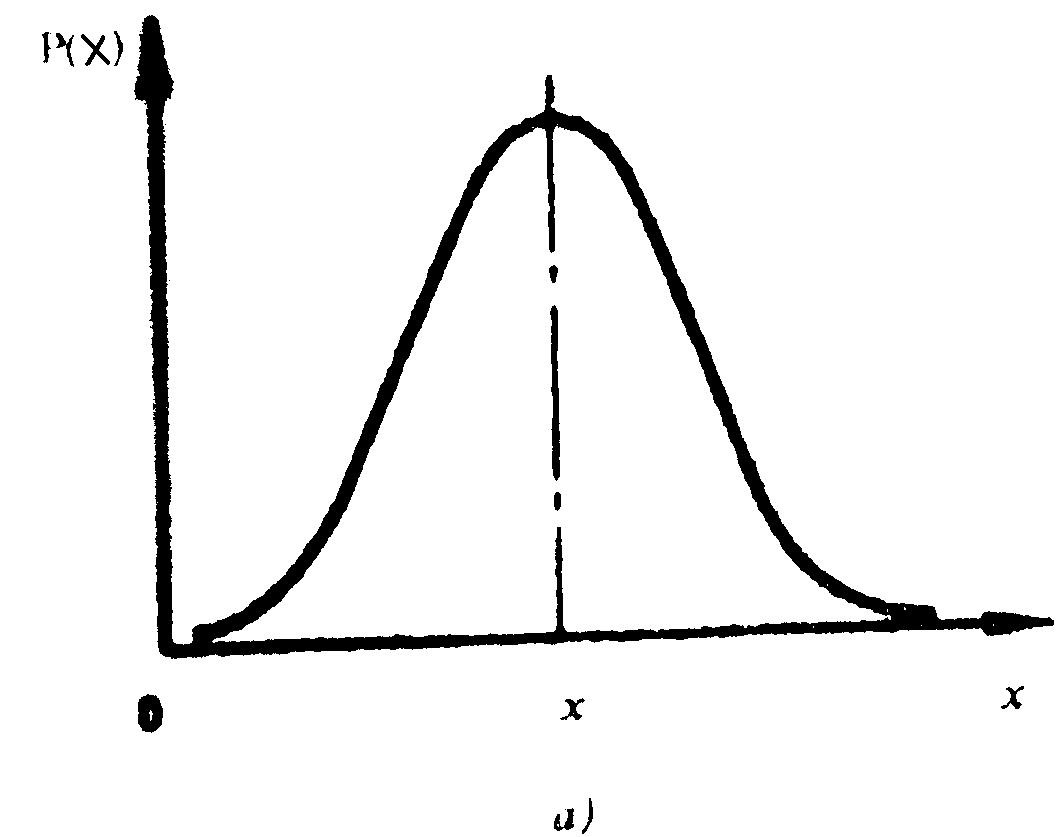
Щільність нормального розподілу

Мірою розсіву значень випадкової величини служить дисперсія D(x), що дорівнює . Дисперсія відхилення від математичного сподівання дискретних розподілів

Неперервних розподіл

Тема 5.4. Визначення грубих похибок

Груба похибка вимірювання – похибка вимірювання, яка значно перевищує очікувану за даних умов похибку. Результати вимірювань, що містять грубі похибки до уваги не беруться. Основні причини цих похибок – помилки дослідника, різка і неочікувана зміна умов вимірювання, несправність приладу та інші. Грубі похибки не завжди легко виявити, для їх виявлення використовують математичні методи.

На практиці зручніше розсіяння характеризувати величиною , яка називається середнім квадратичним відхиленням результата вимірювання від дійсного значення, а до випадкових похибок застосовувати середню квадратичну похибку.

Середня квадратична похибка відповідає характерний точцї кривої нормального розподілу. Абсцисам + і - (рис. 14, 6} відповідають точки перегину кривої. Ймовірність того, що випадкові похибки вимірювання не вийдуть за межі ± . становить 0,6826 наближено 2/3 (див. заштриховану площу).

Математичне сподівання і середнє квадратична похибка  повністю визначають закон розподілу похибок. Як випливає з виразу (25), значення М(х), а отже, (х) можна точно визначити при вскінченно великому числі спостережень n. Тому при обмеженою значенні n результати спостережень характеризують не значення М(х), а середнім арифметичним значенням х:

(28)

Різницю називають відхиленням і-то результату спостереження від середнього арифметичного. Різницю називають випадковою похибкою середнього арифметичного результату спостережень (на відміну від - випадковою похибки будь-якого з результатів спостережень).

Середнє квадратичне відхилення при скінченному чилі вимірювань n характеризується не величиною , а його оцінкою

(29)

а середнє квадратичне відхилення для середнього значення похибки за формулою

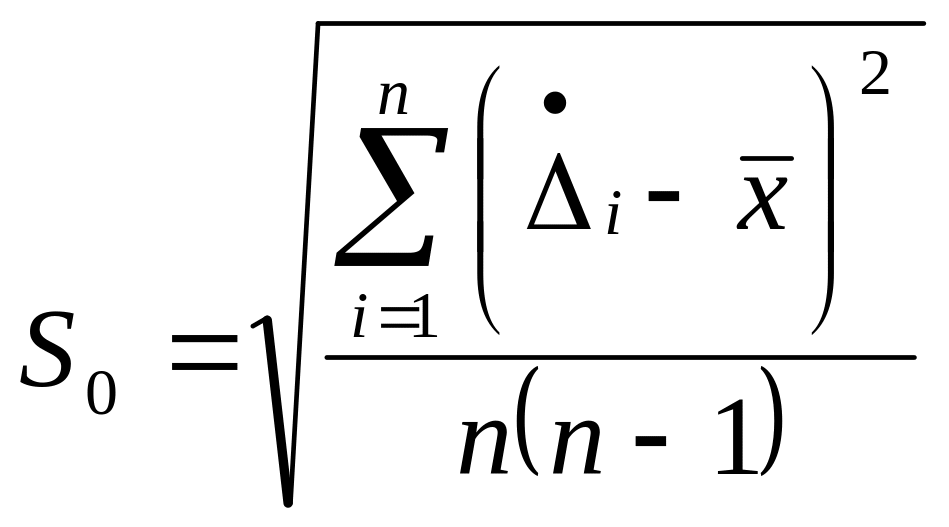(30)

При оцінюванні точності вимірювання не завжди достатньо визначити числове значення похибки (особливо при обмеженому числі n). В таких випадках завдання зводиться до оцінки меж (надійного інтервалу) ,в яких з заданою (надійною) вірогідністю Р лежать значення похибки .

При аналізі результатів спостережень не завжди просто визначити, чи є якесь значення ряду спостережень грубою похибкою Статистичний критерій виявлення грубих похибок використовують для перевірки виду похибки. Якщо умови критерію виконуються то результат спостережень відкидається як анормальний. При невідомому (х) таким критерієм служить співвідношення

Значення для даного n і прийнятої ймовірності P беруть в табл. 5. Якщо то результат Vi відкидається як анормальний.

Приклад 5. Статистичний ряд спостережень при вимірюванні опору тензорезистивного датчика зусилля 9,992; 9,995; 9,997 9,9999; 10,000; 10,001; 10, 003; 10,005; 10,007; 10,121 Ом.

Підозрілим є R₁₀= 10,121 Ом.

Розв'язок:

а) середнє значення

б) середнє квадратичне відхилення

в) г)при п-10 і всіх значеннях Р (табл. 5) тому відкидаємо як грубу похибку.

Таблиця 5. Значення числа для різного числа вимірювань і ймовірності

n	P				n	P
	0.100	0.078	0.050	0.025		0.100	0.075	0.050	0.025
3 4 5 6 7 8 9 10 11	1.15 1.42 1.60 1.74 1.88 1.91 1.98 2.03 2.09	1.15 1.44 1.64 1.79 1.88 1.96 2.04 2.10 2.14	1.15 1.46 1.67 1.85 1.94 2.03 2.11 2.18 2.23	1.15 1.48 1.72 1.93 2.02 2.13 2.21 2.29 2.36	12 13 14 15 16 17 18 19	2.13 2.17 2.21 2.25 2.28 2.31 2.34 2.36	2.20 2.24 2.28 2.32 2.35 2.38 2.41 2.46	2.29 2.33 2.37 2.41 2.44 2.48 2.50 2.56	2.41 2.47 2.50 2.55 2.58 2.62 2.66 2.71