
- •Загальні вимоги до машин та їх елементів
- •Розрахунки при проектуванні і конструюванні
- •Особливості конструкторських розробок
- •Навантаження елементів машин Загальні відомості про навантаження
- •Зовнішні силові фактори
- •Машинобудівні матеріали Сталі, їх застосування і методи зміцнення
- •Чавуни та їхні властивості
- •Сплави кольорових металів
- •Неметалеві матеріали
- •Основні механічні характеристики матеріалів
- •З’єднання деталей машин. Різьбові з’єднання Загальні відомості
- •Кріпильні різьби та їх основні параметри
- •Кріпильні різьбові деталі, їх конструкції та матеріали
- •Стопоріння різьбових з’єднань
- •Елементи теорії гвинтової пари
- •Розрахунок витків різьби на міцність
- •Розрахунок на міцність стержня болта (гвинта)для різних випадків навантаження
- •Шпонкові з’єднання Основні види шпонкових з’єднань та область застосування
- •Розрахунок ненапружених шпонкових з’єднань
- •Зубчасті (шліцеві) та профільні з’єднання Основні типи зубчастих з’єднань і області використання
- •Розрахунок зубчастих з’єднань
- •Профільні з’єднання
- •Зварні з’єднання Особливості з’єднання деталей зварюванням і характеристика з’єднань
- •Типи зварних швів
- •Розрахунок зварних з’єднань на міцність
- •Розрахунок стикового шва
- •Розрахунок кутового шва
- •Р исунок 7. Розрахункова схема для визначення розмірів кутового шва
- •Допустимі напруження для зварних з’єднань
- •Заклепкові з’єднання Конструкції заклепкових з’єднань та області використання
- •Розрахунок заклепкових з’єднань
- •Допустимі напруження у розрахунках заклепкових з’єднань
- •Механічні передачі Призначення механічних передач та їх класифікація
- •Основні співвідношення для кінематичних параметрів і параметрів навантаження механічних передач
- •Фрикційні передачі Загальні відомості та класифікація фрикційних передач
- •Явища ковзання у контакті котків фрикційної передачі
- •Матеріали та конструкції деталей фрикційних передач
- •Натискні пристрої фрикційних передач
- •Види руйнування котків і критерії розрахунку. Допустимі контактні напруження та тиск
- •Геометрія та кінематика передачі
- •Зусилля у циліндричній фрикційній передачі
- •Розрахунок котків на міцність
- •Пасові передачі Загальні відомості та класифікація пасових передач
- •Елементи пасових передач
- •Шківи пасових передач
- •Пружне ковзання паса та кінематика пасової передачі
- •Сили та напруження у вітках пасової передачі. Зусилля та напруження у пасі від його попереднього натягу
- •Зусилля та напруження у вітках при передаванні робочого навантаження
- •Сумарні напруження у перерізах паса
- •Вибір та розрахунок параметрів пасової передачі
- •Розрахунок пасових передач на тягову здатність
- •Розрахунок пасових передач на довговічність
- •Особливості розрахунку плоскопасових передач
- •Особливості розрахунку клинопасових передач
- •Ланцюгові передачі Загальні відомості та класифікація ланцюгових передач
- •Деталі ланцюгових передач. Приводні ланцюги.
- •Зусилля у вітках ланцюгової передачі
- •Критерії працездатності та розрахунок ланцюгових передач
- •Загальні відомості про зубчасті передачі Застосування зубчастих передач та їх класифікація
- •Основні параметри евольвентного зачеплення
- •Конструкції зубчастих коліс та їх виготовлення
- •Точність зубчастих передач
- •Матеріали і термообробка зубчастих коліс
- •Види руйнування зубців та критерії розрахунку на міцність зубчастих передач
- •Циліндричні зубчасті передачі Параметри прямо- та косозубих зубчастих передач
- •Навантаження на зубці циліндричних зубчастих передач
- •Розрахунок зубців на втому і міцність при згині
- •Конічні зубчасті передачі Особливості конічних зубчастих передач
- •Основні параметри конічної прямозубої передачі
- •Навантаження на зубці конічної зубчастої передачі
- •Розрахунок зубців конічних зубчастих передач на контактні втому і міцність, на втому і міцність при згині
- •Черв’ячні передачі Загальні відомості та класифікація черв’ячних передач
- •Параметри черв’ячної передачі. Циліндричні черв’яки
- •Черв’ячні колеса
- •Матеріали і конструкції деталей черв’ячної передачі. Критерії працездатності та розрахунків
- •Проектний розрахунок черв’ячної передачі
- •Розрахунок черв’яка на жорсткість
- •Ккд черв’ячної передачі та її тепловий розрахунок
- •Передача гвинт-гайка
- •Класифікація
- •Загальні відомості
- •Профіль різьби
- •Класифікація гвинтових передач
- •Кут підйому гвинтової лінії та умова самогальмування
- •Коефіцієнт корисної дії передачі гвинт-гайка
- •Методика розрахунку гвинтової пари
- •Вибір матеріалу та розрахунок допустимих напружень гвинта та гайки
- •Проектний розрахунок передачі гвинт-гайка
- •Р исунок 2.2. Профіль та основні розміри трапецеїдальної різьби (гост 9484-81)
- •Перевірка виконання умови самогальмування
- •Осі та вали Загальні відомості. Конструкції та матеріали осей і валів
- •Розрахункові схеми валів та осей. Критерії розрахунку
- •Розрахунок осей на міцність і стійкість проти втомного руйнування
- •Розрахунок валів на статичну міцність
- •Розрахунок валів на втомливу міцність
- •Підшипники кочення Загальні відомості
- •Класифікація, матеріали деталей і точність підшипників кочення
- •Підбір підшипників кочення за статичною та динамічною вантажністю
- •Розрахункове еквівалентне навантаження на підшипники кочення
- •Рекомендації щодо вибору підшипників кочення
- •Підшипники ковзання Загальні відомості
- •Конструкції та матеріали підшипників ковзання
- •Змащування підшипників ковзання
- •Працездатність і режим рідинного тертя у підшипниках ковзання. Критерії працездатності та розрахунку підшипників ковзання
- •Розрахунки підшипників ковзання
- •Муфти приводів Загальні відомості та класифікація муфт
- •Некеровані муфти
- •Керовані муфти
- •Механізми для перетворення руху
- •Р исунок 2. Черв’ячно-рейкова передача
Класифікація гвинтових передач
Передачі гвинт-гайка діляться на передачі ковзання і кочення.
В залежності від компоновки механізму передача гвинт-гайка виконується за наступними кінематичними схемами.
Гвинт одночасно обертається та поступально рухається, гайка нерухома (наприклад знімач – рис. 1.6, а).
Гайка обертається, гвинт рухається поступально (наприклад гвинт регулювання – рис. 1.6, б).
Гвинт обертається, гайка поступально рухається (наприклад ходовий гвинт токарного верстата – рис. 1.6, в).
Гвинт нерухомий, гайка обертається та пересувається поступально (наприклад стіл свердлувального верстата).
Використовують інші конструкції, наприклад телескопічну з двома гвинтовими парами (рис. 1.7).
На рисунку 1.8 зображена гвинтова відводка, яка управляє муфтою. Гвинт 3, що обертається на опорах пересуває гайку 2, яка через важіль 1 виконує керуючі рухи.
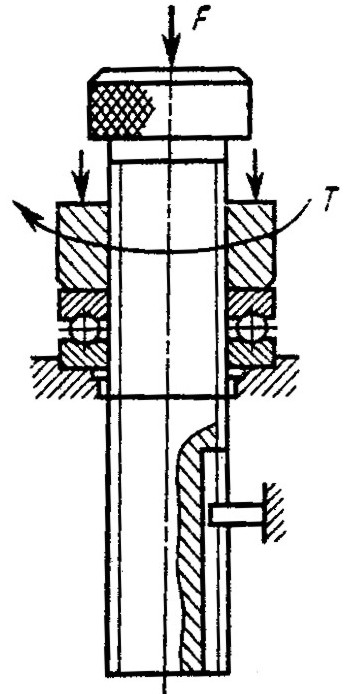
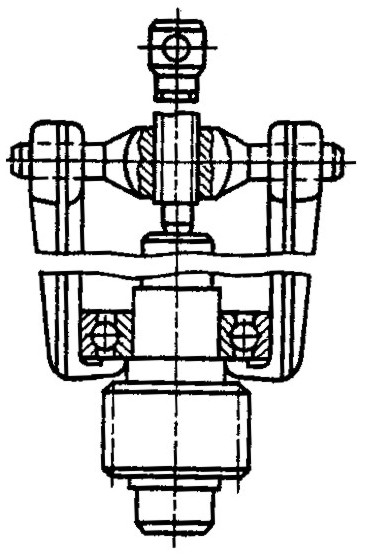
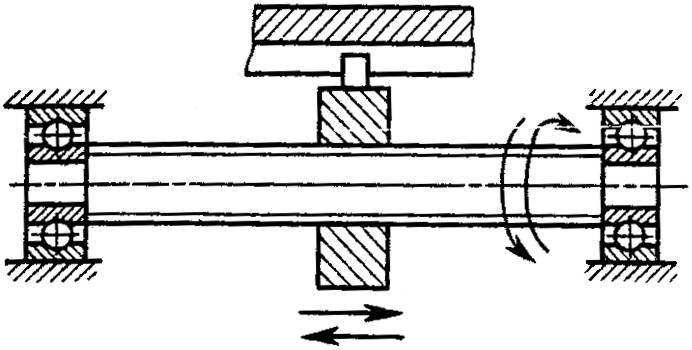
Рисунок 1.6. Приклади виконання передачі гвинт-гайка
Гвинтові механізми мають ручний або механічний приводи: із черв’ячною передачею (рис. 1.9); із зубчастою передачею (рис. 1.10).
М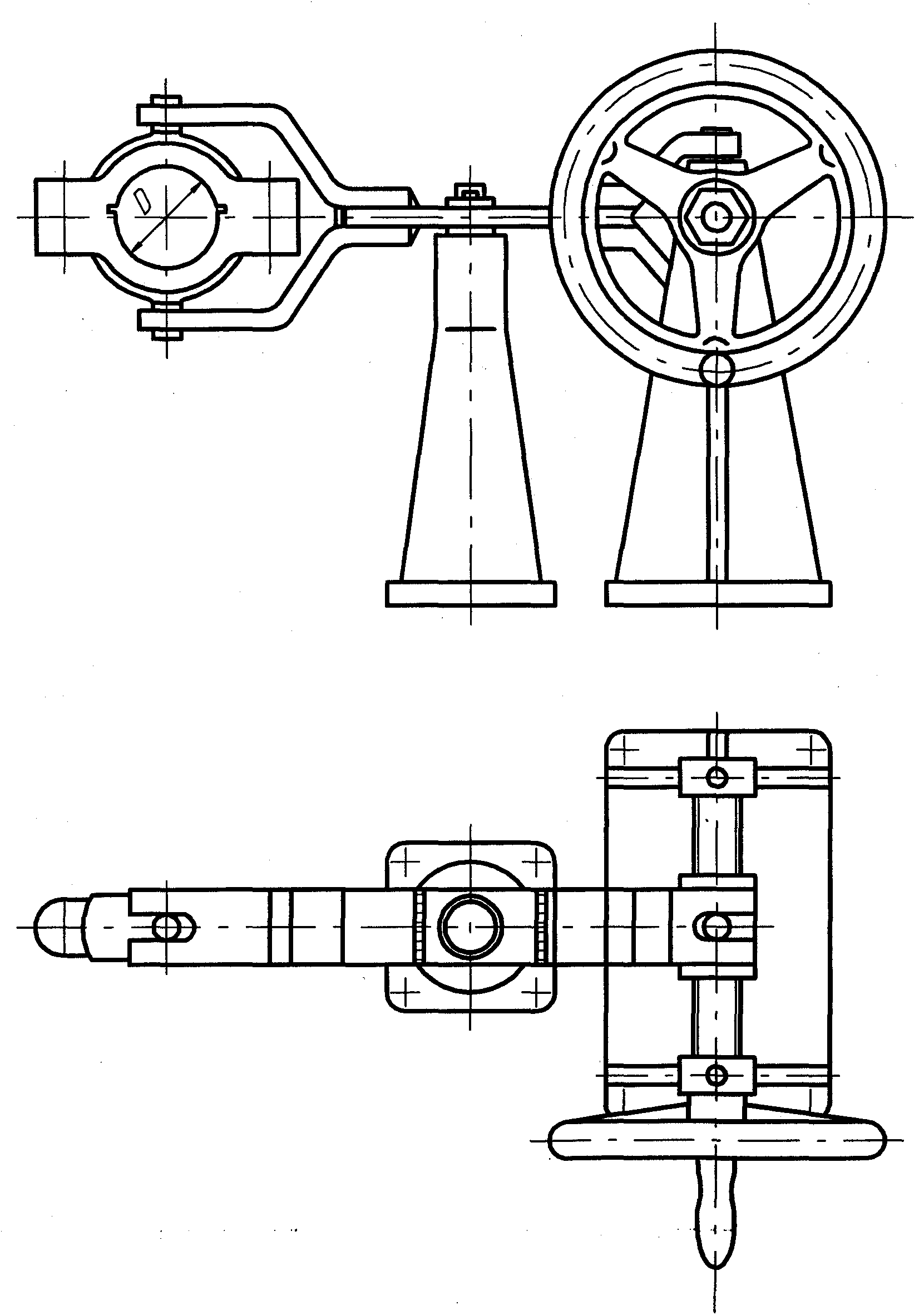 еханізований
домкрат (рис. 1.10) складається з таких
основних деталей: 1
– вантажний гвинт; 2
– гайка вантажного гвинта; 3
– ведучий вал; 4
– ведуче зубчасте колесо; 5
– ведене зубчасте колесо; 6
– чашка; 7
– корпус; 8
– дистанційне керування; 9
– запобіжна стопорна шайба.
еханізований
домкрат (рис. 1.10) складається з таких
основних деталей: 1
– вантажний гвинт; 2
– гайка вантажного гвинта; 3
– ведучий вал; 4
– ведуче зубчасте колесо; 5
– ведене зубчасте колесо; 6
– чашка; 7
– корпус; 8
– дистанційне керування; 9
– запобіжна стопорна шайба.
Р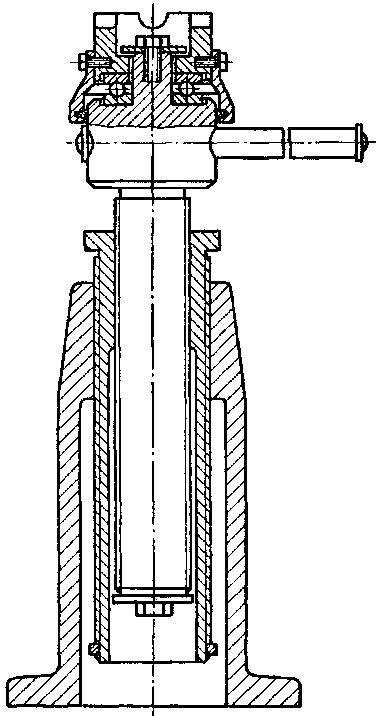 исунок
1.7. Телескопічний домкрат Р
исунок
1.7. Телескопічний домкрат Р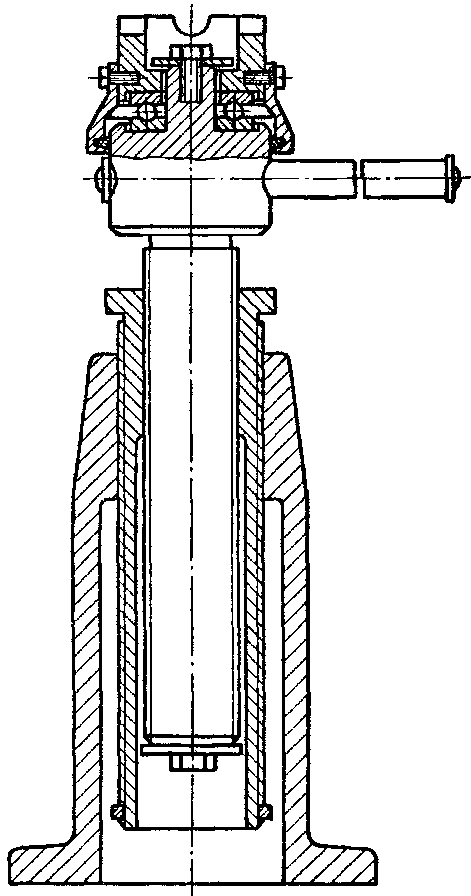 исунок
1.8. Гвинтова відводка
исунок
1.8. Гвинтова відводка
Для забезпечення тривалого, без спрацювання, режиму роботи гвинтових механізмів необхідно забезпечувати наявність стійкого шару мастила у спряженні витків, товщина якого повинна перевищувати складений розмір шорсткості поверхонь.
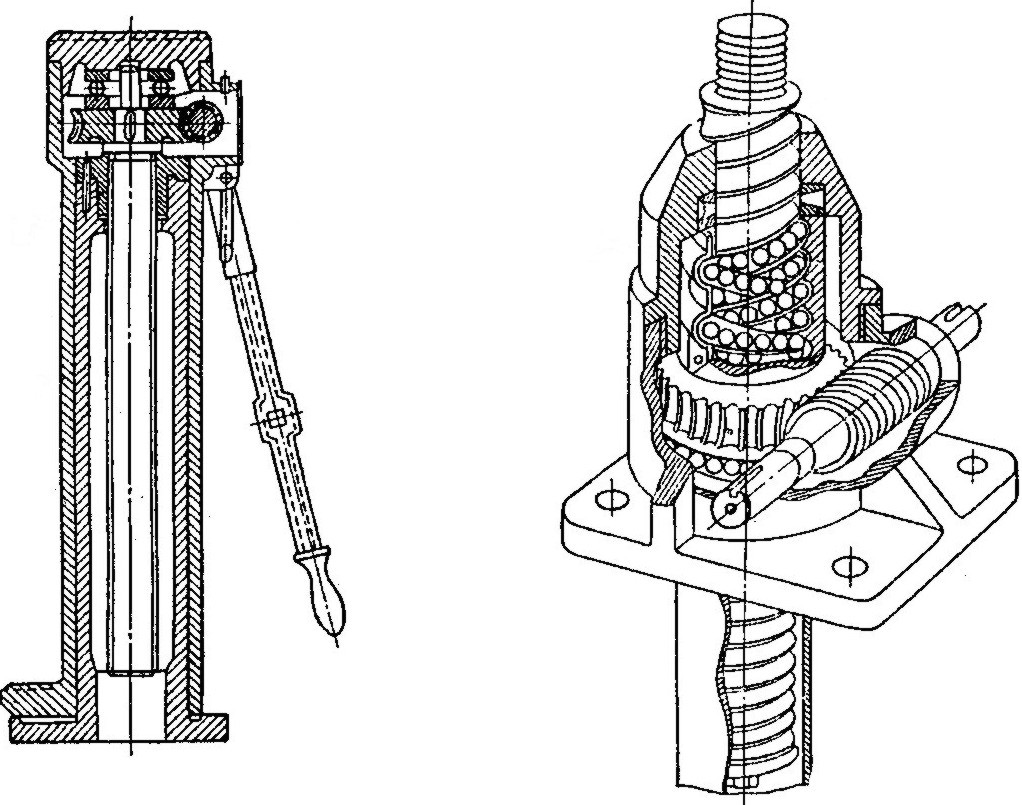
Рисунок 1.9. Ручний привод механізму із черв’ячною передачею
Широкого розповсюдження набувають кулькові гвинтові пари, в яких тертя ковзання заміщене тертям кочення (рис. 1.1, г, 1.9).
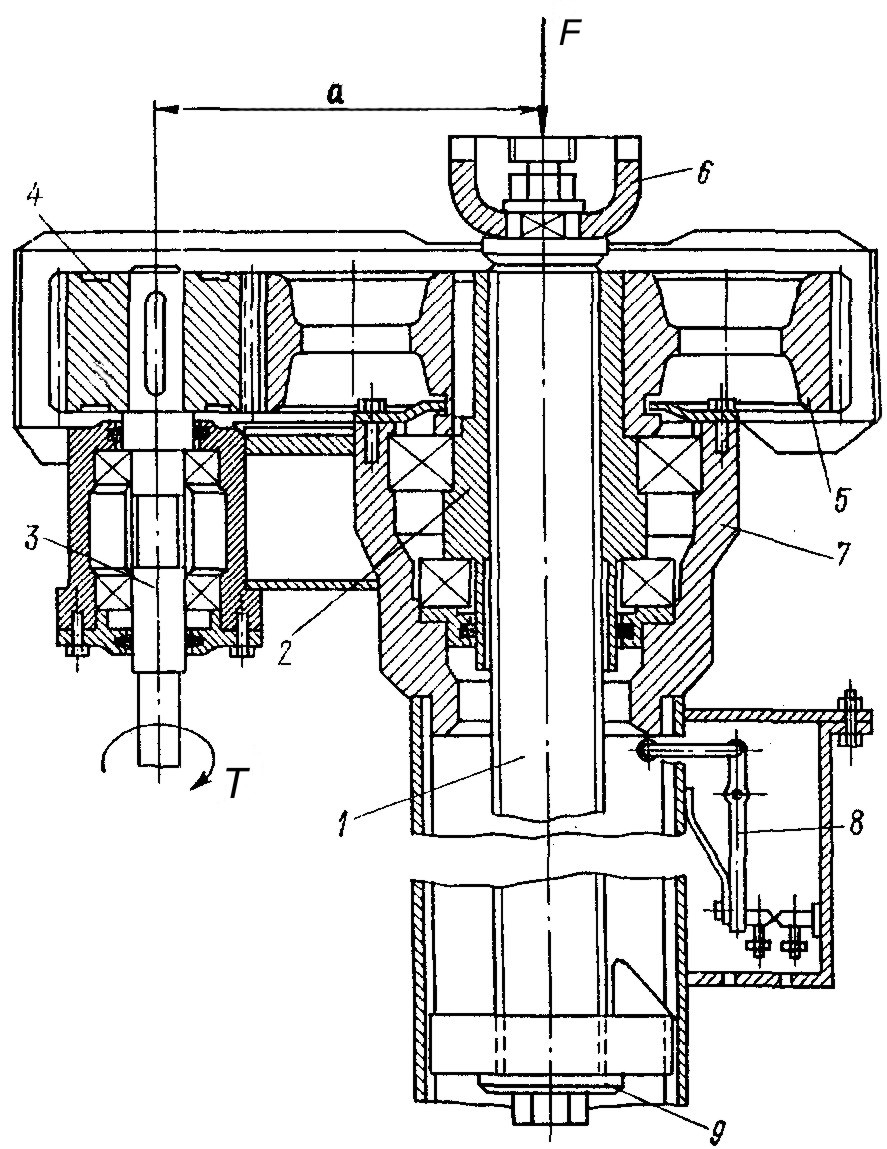
Рисунок 1.10. Механічний привод механізму із зубчастою передачею
Такий механізм має високий
ККД (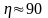 %),
а коефіцієнт тертя кочення
%),
а коефіцієнт тертя кочення
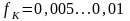 ,
що значно менше за коефіцієнт тертя при
ковзанні витків (
,
що значно менше за коефіцієнт тертя при
ковзанні витків (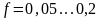 ).
).
Існує можливість усунення осьових та радіальних зазорів у передачі, підвищення точності верстатів з програмним керуванням, вимірювальних пристроїв, роботів, механізмів керування шасі та стабілізаторів літаків, дистанційного керування атомної техніки та ін.
Кут підйому гвинтової лінії та умова самогальмування
Вибір кроку різьби залежить
від умови самогальмування
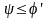 .
Необхідно пам’ятати,
що із зменшенням кроку різьби зменшується
не тільки кут підйому гвинтової лінії,
а і коефіцієнт корисної дії гвинтової
пари. Тому слід приймати середнє значення
кроку різьби для обраного діаметра.
.
Необхідно пам’ятати,
що із зменшенням кроку різьби зменшується
не тільки кут підйому гвинтової лінії,
а і коефіцієнт корисної дії гвинтової
пари. Тому слід приймати середнє значення
кроку різьби для обраного діаметра.
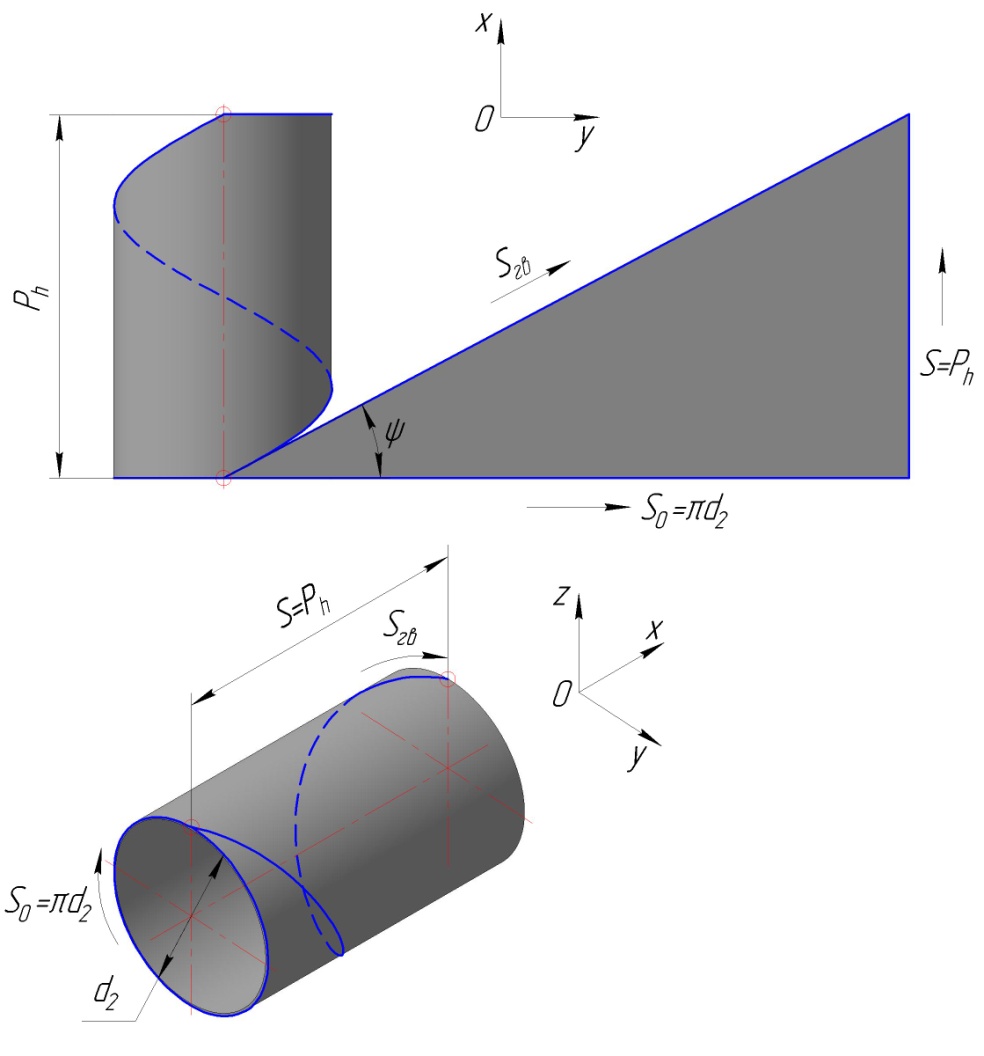
Рисунок 1.11. Розгортка гвинтової лінії
Кут підйому гвинтової лінії показаний на розрахунковій схемі (рис. 1.11). Тут
виконана
проекція гвинтової лінії діаметра
на площину
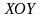 ,
яка має синусоїдальний вигляд. Рух по
гвинтовій траєкторії є комбінацією
обертального та поступального пересування,
тобто за один повний оберт з довжиною
,
яка має синусоїдальний вигляд. Рух по
гвинтовій траєкторії є комбінацією
обертального та поступального пересування,
тобто за один повний оберт з довжиною
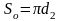 ,
мм
(перший катет трикутника), (1.1)
,
мм
(перший катет трикутника), (1.1)
точка профілю різьби пересувається поступально в осьовому напрямку на відстань
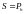 ,
мм
(другий катет),
,
мм
(другий катет),
долаючи повний шлях по гвинтовій траєкторії
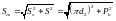 ,
мм
(гіпотенуза трикутника), (1.2)
,
мм
(гіпотенуза трикутника), (1.2)
де
– середній діаметр різьби, мм;
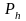 – хід гвинта або крок
,
мм; якщо
різьба з одним
– хід гвинта або крок
,
мм; якщо
різьба з одним
заходом.
Кут підйому гвинтової лінії – це кут між розгортками гвинтової лінії та кола з середнім діаметром (гіпотенузою та першим катетом), який ми бачимо на площині без викривлень.
Найпростіше його обчислити через функцію тангенсу, тобто через катети
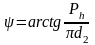 . (1.3)
. (1.3)
У подальшому, оскільки розглядається самогальмівна різьба з одним заходом, замість ходу у формулі (1.3) вказуємо крок
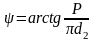 . (1.4)
. (1.4)
Зведений кут тертя
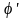 є важливим геометричним параметром
теорії гвинтової пари (рис. 1.12).
є важливим геометричним параметром
теорії гвинтової пари (рис. 1.12).
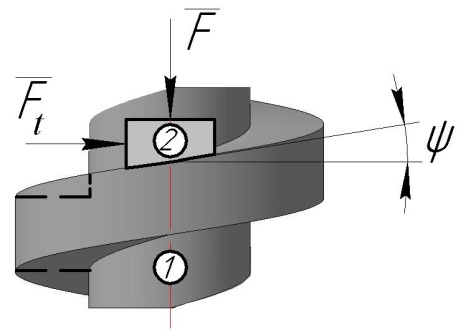
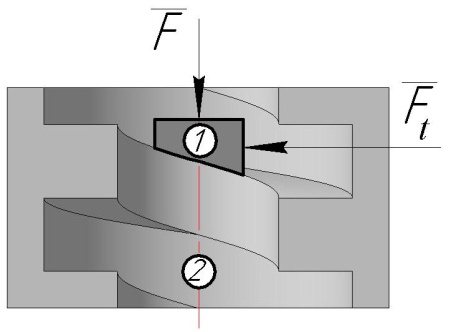
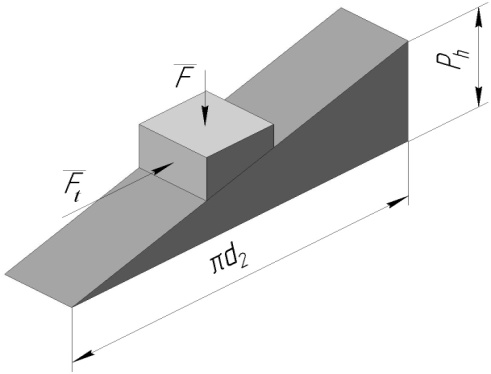
а б
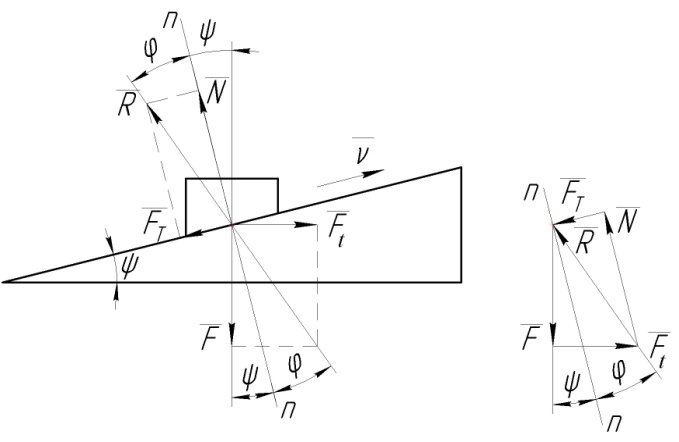
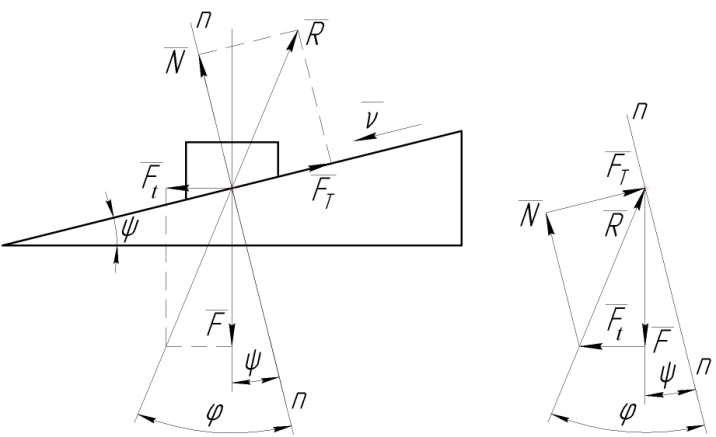
в г
Рисунок 1.12. Кінематика гвинтової пари (прямокутна різьба)
Схема 1.12, а складена для елементу гайки 2, яка рухається по різьбі гвинта 1 (механізми подачі), схема 1.12, б – для елементу гвинта 1, який пересувається по різьбі гайки 2 (домкрат). Різьба приймається прямокутна. Її елементи розглядаються, як повзуни,
що пересуваються по нахиленій площині з кутом нахилу .
Активні зусилля, що діють на елемент: – осьове зусилля (вага вантажу для домкрата, зусилля демонтажу підшипника – для знімача), Н; – колова рушійна сила, Н.
Реактивні зусилля:
 – нормальна реакція, Н;
– нормальна реакція, Н;
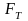 – сила тертя, Н;
– повна реакція, Н.
– сила тертя, Н;
– повна реакція, Н.
З плану сил маємо 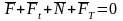 ;
(1.5)
;
(1.5)
звідки колова сила для прямокутної різьби
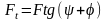 ,
Н; (1.6)
,
Н; (1.6)
якщо елемент рухається у напрямку, протилежному силі (рис. 1.12, в);
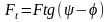 ,
Н; (1.7)
,
Н; (1.7)
якщо елемент рухається у напрямку сили (рис. 1.12, г);
тут
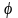 – кут тертя для прямокутної різьби
– кут тертя для прямокутної різьби
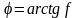 ; (1.8)
; (1.8)
де – коефіцієнт тертя, який залежить від обраного матеріалу гвинта та гайки (табл. 3)
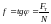 ; (1.9)
; (1.9)
За умови 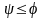 ;
(1.10)
;
(1.10)
передача з прямокутною різьбою буде самогальмівною.
Зведений кут тертя визначається для трикутних та трапецеїдальних різьб за формулою (1.11), виведення якої буде показаний нижче
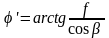 ; (1.11)
; (1.11)
тут – кут нахилу робочої поверхні витка.
Ця формула є загальною для
всіх профілів, а прямокутна різьба з
кутом
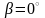 представляє окремий випадок
представляє окремий випадок
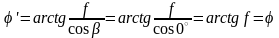 . (1.12)
. (1.12)
Тобто кут тертя дорівнює
зведеному куту
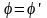 .
.
У випадках інших різьб маємо:
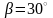 – для метричної різьби;
– для метричної різьби;
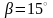 – для трапецеїдальної різьби;
– для трапецеїдальної різьби;
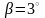 – для упорної різьби;
– для упорної різьби;
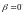 – для прямокутної різьби.
– для прямокутної різьби.
Формула (1.11) отримується за розрахунковою схемою (рис. 1.13).
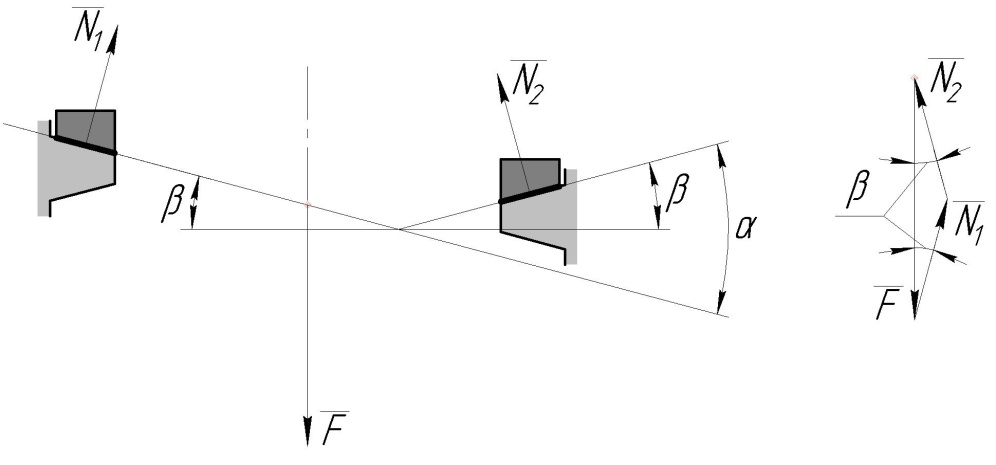
Рисунок 1.13. Кінематика гвинтової пари (трапецеїдальна різьба)
За цією моделлю елемент різьби
розглядається, як клиновий повзун, що
рухається по нахиленому під кутом
жолобі з кутом між стінками
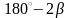 .
Активній силі
протидіють дві рівних реакції
.
Активній силі
протидіють дві рівних реакції
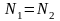 .
.
За планом сил маємо
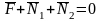 . (1.13)
. (1.13)
Загальна сила тертя
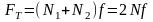 ,
Н. (1.14)
,
Н. (1.14)
З трикутника сил отримуємо
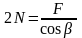 ,
Н. (1.15)
,
Н. (1.15)
Тоді зусилля тертя
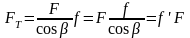 ,
Н; (1.16)
,
Н; (1.16)
де
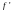 – зведений коефіцієнт тертя
– зведений коефіцієнт тертя
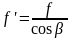 . (1.17)
. (1.17)
Остаточно для всіх різьб маємо
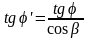 . (1.18)
. (1.18)
тобто ми довели формулу (1.11) .
Колове зусилля надалі
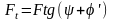 ,
Н;
(1.19)
,
Н;
(1.19)
якщо елемент рухається у напрямку, протилежному силі ;
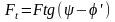 ,
Н; (1.20)
,
Н; (1.20)
якщо елемент рухається у напрямку сили .
Умова самогальмування для всіх різьб набуває вигляду
. (1.21)
Аналізуючи формули (1.4) та (1.11), робимо висновок, що із збільшенням кута нахилу робочої поверхні витка зростає зведений кут тертя, тобто збільшується імовірність виконання умови (1.21). До речі, всі кріпильні різьби самогальмівні. Факт зростання із збільшенням дає можливість збільшувати крок , а з ним і ККД передачі.
Якщо умова самогальмування
не виконується, тобто
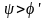 ,
необхідно прийняти різьбу з меншим
кроком та середнім діаметром
,
мм;
не меншим за розрахунковий.
,
необхідно прийняти різьбу з меншим
кроком та середнім діаметром
,
мм;
не меншим за розрахунковий.
Самогальмівні передачі застосовуються для перетворення обертального руху у поступальний, при цьому гарантована відсутність пересувань під дією осьового статичного навантаження, тобто у самогальмівних передачах вантаж, який піднято не буде самостійно опускатися, що робить зайвим використання гальмівних пристроїв.
Якщо у гвинтової передачі
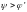 ,
вона є несамогальмівною.
,
вона є несамогальмівною.
За умови
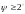 і
і
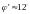 гвинтовий механізм можна використовувати
для перетворення поступального руху в
обертальний.
гвинтовий механізм можна використовувати
для перетворення поступального руху в
обертальний.
Довжина гвинтового пересування за один повний оберт визначається точно за формулами (1.2), (1.22) та рис. 1.11
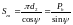 ,
мм; (1.22)
,
мм; (1.22)
або
наближено, враховуючи те що при
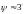 ;
;
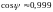
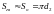 ,
мм. (1.23)
,
мм. (1.23)
