Контрольні питання

1. Які групи впливів та умови роботи необхідно враховувати при розрахунку надійності електрообладнання в реальних умовах експлуатації?

2. Основні чинники, що впливають на значення інтенсивності відмов елементів.

3. Розрахунок коефіцієнта навантаження для різних типів електрообладнання.

4. Як визначається фактична інтенсивності відмов елемента з урахуванням основних чинників впливу?

5. У чому сутність методу середньогрупових інтенсивностей відмов?

Література: [2, с. 172-182; 3, с. 129-167; 5, с 35-40, 47-50].

Практичне заняття №5

Тема. Розрахунок надійності резервованих систем.

Мета: оволодіти навичками розрахунку надійності систем з різними типами резервування.

Короткі теоретичні відомості

Резервуванням називається введення надлишкової кількості елементів для підвищення надійності функціонування системи, пристрою тощо. На рис. 5.1 подана класифікація існуючих типів резервованих систем.

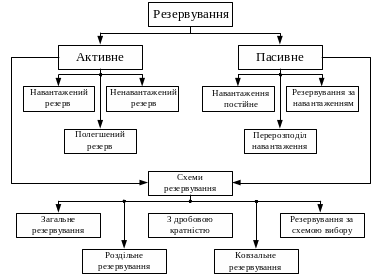
Рисунок 5.1 – Класифікація резервованих систем

Розглянемо розрахунок найбільш характерних логічних схем резервованих систем.

Пасивне резервування з постійним навантаженням.

– імовірність безвідмовної роботи;

– середній час напрацювання до відмови;

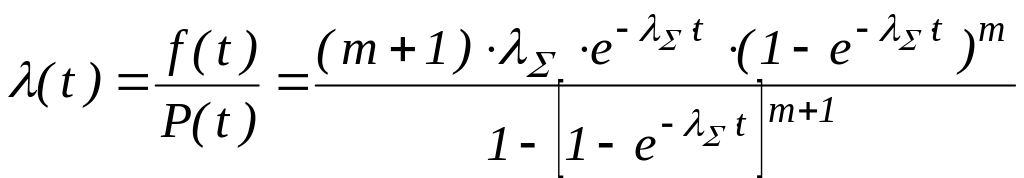– інтенсивність відмов системи;

де – кратність резервування.

Активне резервування з ненавантаженим резервом.

– імовірність безвідмовної роботи системи,

де – інтенсивність відмов основної системи; – інтенсивність відмов резервної системи.

У випадку, коли резервна і основна системи рівно надійні отримаємо:

– імовірність безвідмовної роботи при кількості т резервних елементів.

Активне резервування з полегшеним резервом.

– імовірність безвідмовної роботи системи,

де – інтенсивність відмов резервної системи в “розігрітому” стані; – інтенсивність відмов резервної системи після її підключення за допомогою перемикача.

Активне резервування з навантаженим резервом.

– імовірність безвідмовної роботи системи.

Враховуючи, що , , маємо: . Отже, активне резервування з навантаженим резервом при абсолютно надійних перемикачах можна розглядати як пасивне резервування з постійним навантаженням.

Ковзальне резервування.

– імовірність безвідмовної роботи системи ( – інтенсивність відмов перемикача).

Якщо резервний і елементи основної частини рівно надійні, то вираз набуде вигляду: .

При кількості резервних елементів т: .

Приклади розв’язання завдань

Приклад 5.1. Система складається з N=100 елементів, які з’єднані логічно послідовно. Інтенсивність відмов такої системи 1/год. За допомогою пасивного резервування забезпечити надійність системи протягом t=1000 год, рівною .

Розв’язок:

Визначимо ймовірність безвідмовної роботи нерезервованої системи:

.

Розглянемо загальне пасивне резервування з постійним навантаженням: . Виконавши логарифмування даного виразу, визначимо кратність резервування:

.

Таким чином, для забезпечення необхідного рівня надійності потрібно не менш як шестикратне резервування аналогічними системами.

Розглянемо розділене пасивне резервування з постійним навантаженням. Знайдемо середнє значення інтенсивності відмов одного елемента:

1/год.

Середнє значення ймовірності безвідмовної роботи одного елемента:

.

Імовірність безвідмовної роботи резервованої системи:

.

Тоді кратність резервування визначимо:

.

Таким чином, при розділеному резервуванні потрібний рівень надійності забезпечиться при однократному резервуванні.

Приклад 5.2. Блок живлення електропривода складається з двох однотипних тиристорних перетворювачів і ґенератора постійного струму. Тиристорні перетворювачі з’єднані за схемою дублювання з постійним навантаженням. Для роботи блока живлення необхідно, щоб працездатними були ґенератор і хоча б один тиристорний перетворювач. Інтенсивність відмов тиристорного перетворювача 1/год, ґенератора 1/год. Розрахувати ймовірність безвідмовної роботи протягом 5 годин та інтенсивність відмов блока живлення.

Розв’язок:

Логічна схема з’єднань блока живлення має вигляд ( рис. 5.2):

Рисунок 5.2 – Логічна схема блока живлення

Імовірність безвідмовної роботи такої логічної схеми дорівнює:

.

З урахуванням t=5 год отримаємо:

.

Для визначення інтенсивності відмов вираз густини напрацювання до відмови запишемо таким чином:

.

Тоді вираз інтенсивності відмов буде:

.

Для t=5 год отримаємо 1/год.

Приклад 5.3. Для підвищення надійності блока живлення електропривода, який складається з ґенератора і тиристорного перетворювача, застосовано дублювання з постійним навантаженням. Необхідно порівняти ймовірності відмов дубльованого блока живлення і блока живлення, в якому дубльований тільки тиристорний перетворювач. Для розрахунку використати дані задачі 2.

Логічна схема дубльованого блока живлення має вигляд рис. 5.3:

Рисунок 5.3 – Логічна схема дубльованого блока живлення

Імовірність відмов дубльованого блока живлення дорівнює:

.

Імовірність відмов блока з дубльованими тиристорними перетворювачами: .

Таким чином, відношення ймовірностей відмов становить:

.

Отже, при дублюванні всього блока живлення надійність збільшується в 15 разів.

Приклад 5.4. Система електропривода, яка розрахована на роботу протягом 20 годин, має інтенсивність відмов 1/год. Визначити ймовірність безвідмовної роботи у випадку активного резервування з абсолютно надійним перемикачем.

Розв’язок:

Для розв’язку такої задачі використовуємо залежність імовірності безвідмовної роботи для випадку активного резервування з ненавантаженим резервом, якщо основна і резервна системи рівно надійні:

.

Приклад 5.5. Розрахувати ймовірність безвідмовної роботи резервованої системи, якщо інтенсивність відмов перемикача 1/год, а інтенсивність відмов основної та резервної системи становлять 1/год. Резервна система знаходиться у ненавантаженому резерві, а t_i=100 год.

Розв’язок:

Для розрахунку використовуємо вираз для ймовірності відмов при активному резервуванні з ненавантаженим резервом, якщо основна і резервна системи рівно надійні:

.

Приклад 5.6. Турбіна має інтенсивність відмов 1/год. Вона зарезервована іншою турбіною, яка, перебуваючи в “розігрітому” стані, має інтенсивність відмов 1/год. Після підключення резервованої турбіни за допомогою абсолютно надійного перемикача, інтенсивність відмови резервної турбіни становить 1/год. Розрахувати ймовірність безвідмовної роботи резервованої системи протягом часу год.

Розв’язок:

Дана система має полегшений резерв, тому використовуємо для розрахунку формулу:

.

Приклад 5.7. Система складається з блока живлення, системи керування та силового обладнання. Блок живлення складається з двох працюючих джерел живлення і одного джерела в ненавантаженому резерві. Перемикач вважається абсолютно надійним. Система керування має пасивний резерв з постійним навантаженням. Силове обладнання містить три блоки і резерву не має. Відомі інтенсивності відмов: джерела живлення , системи керування , силових блоків , , . Записати вирази для розрахунку ймовірності безвідмовної роботи системи.

Розв’язок:

Логічна схема для розрахунку надійності наведена на рис. 5.4.

Цю схему зручно розбити на три ділянки: І – блок живлення, в якому реалізовано ковзальне резервування; ІІ – система керування з пасивним резервом при постійному навантаженні; ІІІ – нерезервовані силові блоки. Імовірність безвідмовної роботи системи: ,

де ; ; .

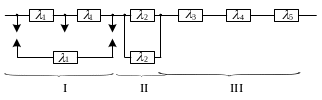
Рисунок 5.4 – Логічна схема системи