2. Точковий імпульс.

Границя фізичного імпульсу при називається точковим імпульсом.

вибираємо так, щоб . Якщо

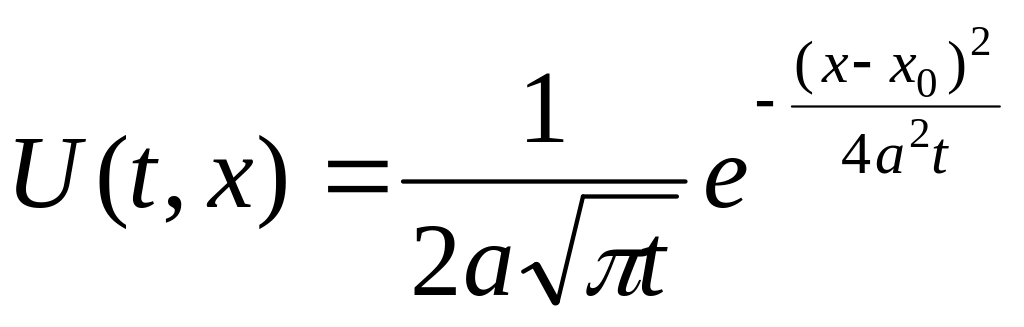- функція Гріна для рівняння теплопровідності.

Точковий імпульс вказує розподіл температури в нескінченному стержні, якщо в початковий момент в точці поставити теплове джерело з потужністю 1.

В границі функція, графік якої зображена на рис.1, переходить в так звану - функцію Дірака.

- функція задовольняє певні властивості.

1.

2. .

Висновок.

При розв’язанні задачі Коші для одномірного рівняння теплопровідності виникає необхідність введення нових функцій (узагальнених).

9.Теплопровідність у скінченому стержні.

Якщо стержень скінчений (деякий відрізок осі ), то для постановки задачі про поширення тепла в ньому, крім рівняння

, (1)

початкової умови , (2)

потрібно задати тепловий режим на кінцях стержня, тобто при і , який визначається межовими умовами

, (3)

тому задача носить назву крайової задачі.

9.1 Крайова задача

Припускаємо, що бічна поверхня стержня тепло ізольована і

Умова говорить, що температура на лівому кінці підтримується і дорівнює 0.Умова (3) говорить про теплообмін на правому кінці.

Знак «-» вказує на те, що градієнт температури спрямований по внутрішній нормалі до поверхні. Швидкість зміни температури вздовж стержня пропорційна різниці температур стержня і середовища.

l- довжина стержня.

0 l x

Це одна з найпростіших крайових задач для розповсюдження тепла у скінченому стержні. Розв’язується задача методом Фур’є.

Метод Фур’є.

Шукається функція , яка залежить від двох змінних

;

після виконання необхідних процедур дістанемо:

Використаємо межові умови:

1)

2)

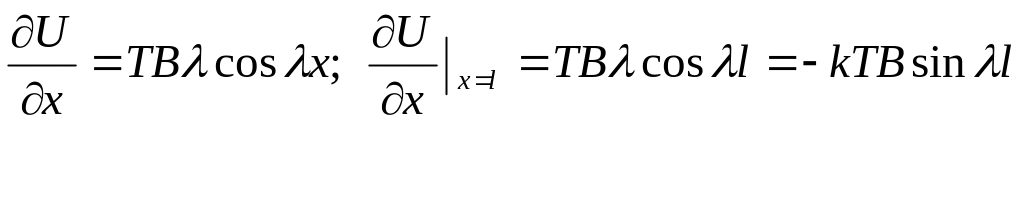
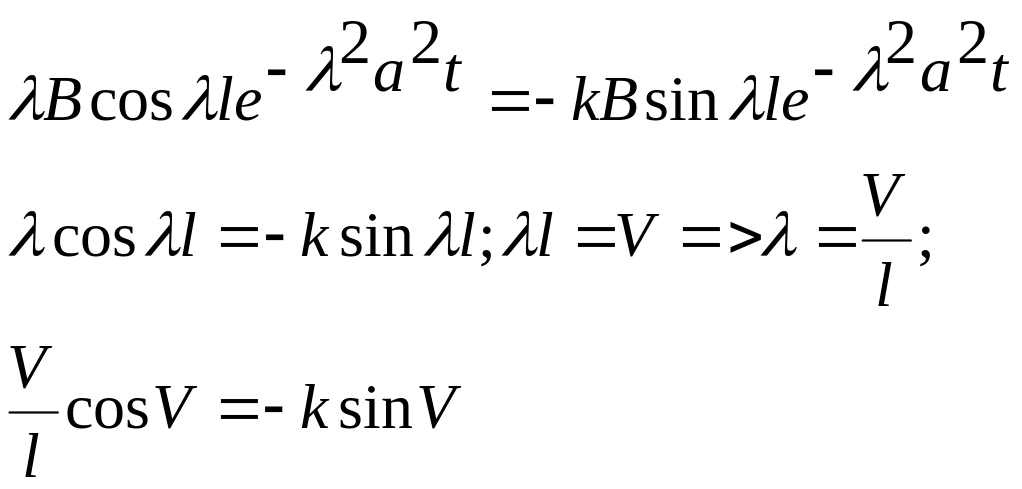
Власні числа подаються через корені трансцендентного рівняння:

Отримали трансцендентне рівняння, яке має безліч коренів, які вказують на власні числа

y

V

- корені рівняння

- відповідні значення

.

Дістанемо зчисленну множину розв’язків :

.

Розв’язком рівняння буде також функція

Використовуємо початкову умову(2):

- коефіцієнти Фур’є для функції за системою , на відрізку від 0 до .

Можна довести, що система функцій ортогональна на відрізку

Множимо зліва і справа останню рівність на і інтегруємо:

.

. (**)

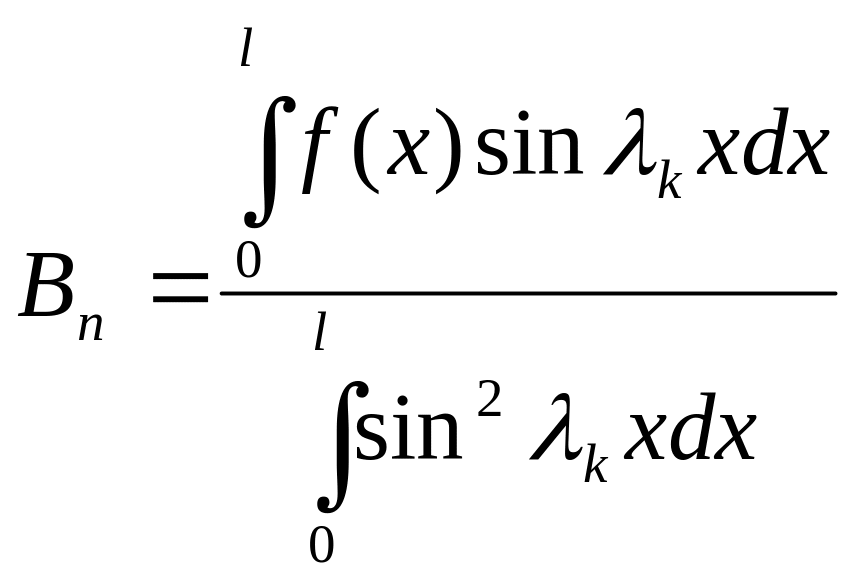Висновок:

Розв’язок крайової задачі для скінченого стержня подається у формі ряду (*), де подаються формулою (**).