Автори Босовський М.В., Демченко О.Г.

Предмет математичної фізики.

Математична фізика вивчає функціональні рівняння що описують найважливіші фізичні процеси і явища. Це диференціальні рівняння з частинними похідними, інтегральні рівняння та інтегродиференціальні рівняння.

1.Основні поняття і символіка:

, … або x,y,z,t... - незалежні змінні;

U,V,W, - функції незалежних змінних;

…, …, - частинні похідні.

О.1 Рівняння, що містить хоча б одну частинну похідну від шуканої функції, називається диференціальним рівнянням з частинними похідними.

Це рівняння можна записати так:

F ( … ; , … …)=f ( … ), (1)

якщо то рівняння називається однорідним.

О.2 Порядок старшої похідної, що входить в рівняння, називається порядком рівняння.

О.3 Якщо порядок рівняння дорівнює , і функція неперервна, то розв’язком рівняння(1) називається - раз неперервно-диференційовна функція, яка рівняння перетворює в тотожність.

Лінійні диференціальні рівняння II порядку.

О.4 Рівняння називається лінійним, якщо шукана функція і всі її похідні входять до рівняння в першому степені, а коефіцієнти рівняння є функціями незалежних змінних.

Лінійне диференціальне рівняння II-го порядку з двома змінними записується так:

+ + + + + = (2)

A, B, C, D, E, K, - функції від x, y.

+ + -головна частина рівняння, вона є лінійним диференціальним оператором II-го порядку. Позначається:

LU=AU +2BU +CU ;

+ + =

Матриця оператора:

- симетрична, тому = (транспонована матриця)

О.5 Диференціальне рівняння називається квазілінійним, якщо воно лінійне відносно найстарших похідних.

Приклади:

1. - нелінійне диференційне рівняння.

2. - квазілінійне диференціальне рівняння III-го порядку.

3. - лінійне однорідне диференціальне рівняння IV- го порядку від незалежних змінних.

4. - нелінійне однорідне диференціальне рівняння IV- го порядку від двох незалежних змінних.

2.Заміна змінних.

Постановка задачі: У рівності переходимо

від змінних x, y до за формулами

(3)

Вважаємо, що двічі неперервно-диференційовані. Встановити, як при цьому змінюється оператор LU.

Позначимо через і матрицю Якобі і транспоновану матрицю:

; .

Вважаємо, що перетворення координат (3) не вироджене, тобто .

Теорема.

При перетворенні координат за формулами (3) оператор LU перетвориться за правилом:

, (4)

де 1) має матрицю і структуру, аналогічну L,

з частинними похідними по та

,

,

, (5)

;

2) та результат застосування оператора до функцій та :

(6)

Доведення.

Доводимо теорему прямим способом: знаходимо за правилом диференціювання складної функції, підставляємо в рівняння, перегруповуємо доданки і показуємо, що ліва частина дорівнює правій.

1) ;

2)

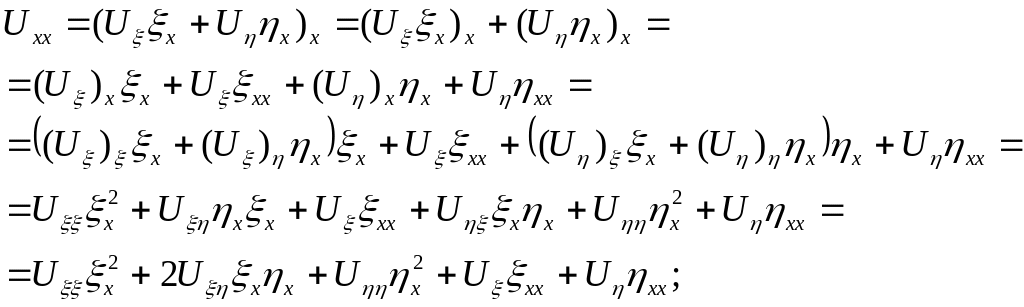
3) Аналогічно дістаємо:

4)

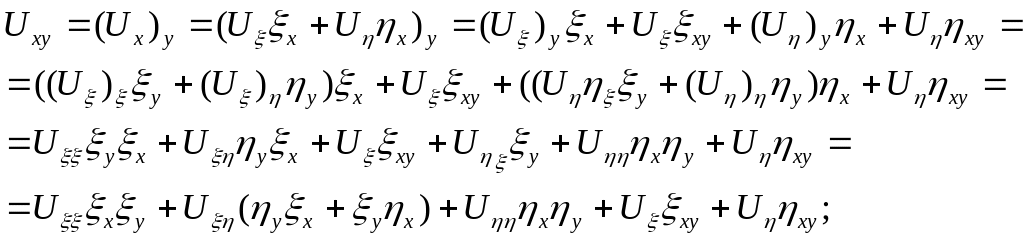
5)

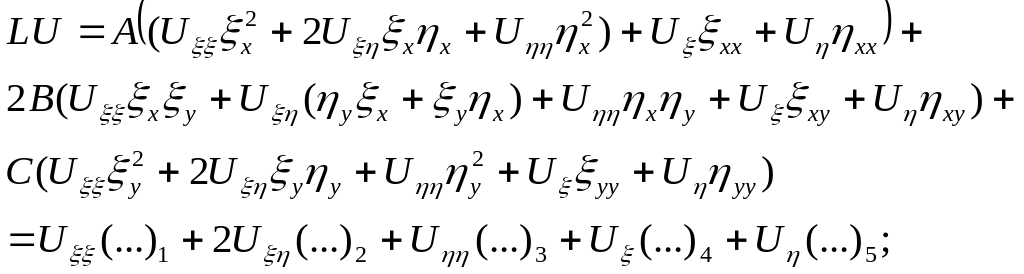
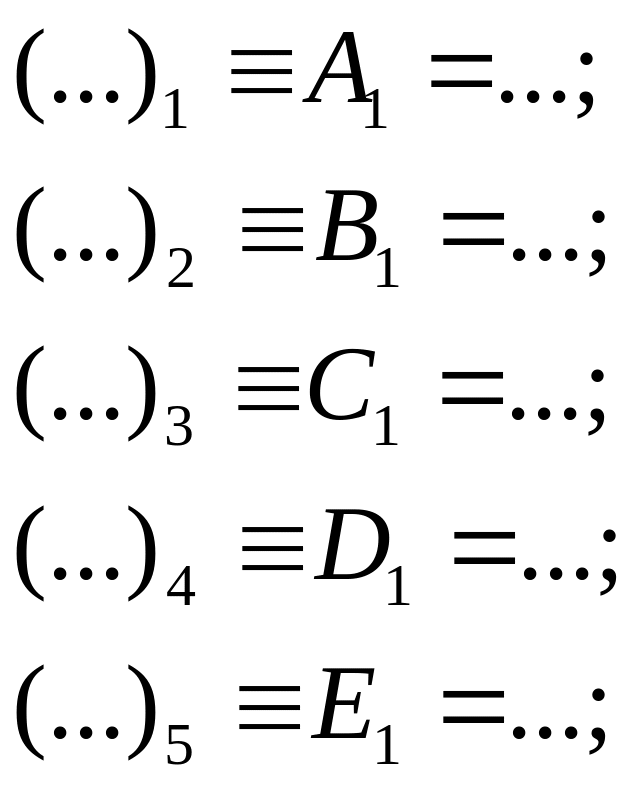
6)

тому

- симетрична:

а)

б)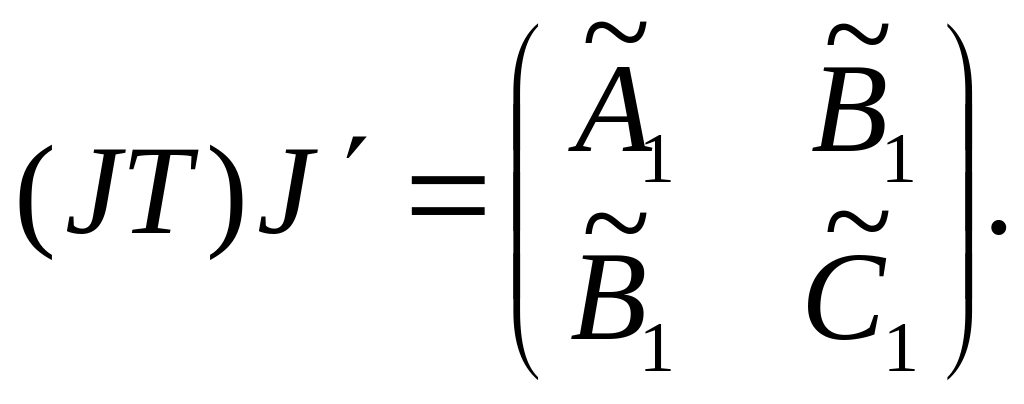

7) Порівнюємо і (відповідно)

Висновок:

,

,

.

3.Класифікація диференціальних рівнянь в частинних похідних II-го порядку від двох незалежних змінних.

О. Якщо В -АС <0 то рівняння (2) називається еліптичним,

якщо В -АС _>0 то рівняння (2) називається гіперболічним,

якщо В -АС =0 то рівняння (2) називається параболічним.

Зауваження.

Класифікація рівняння подається для заданої точки. Якщо А, В, С постійні на всій площині, то рівняння не змінює тип на всій площині.

Приклад 5. Визначити тип рівняння.

1. - рівняння Лапласа.

А=1, В=0, С=1 , В -АС =0-1=-1<0 – еліптичне рівняння

Теорема.

При не виродженому перетворенні координат тип рівняння не змінюється.

Доведення (самостійно).

Якщо функція U залежить від n змінних то класифікація рівнянь II-го порядку проводиться за кількістю додатних, від’ємних і нульових власних чисел матриці.

- корені рівняння є власними числами оператора.

Оскільки матриця Т симетрична то власні числа дійсні.

Якщо серед власних чисел є - додатніх, - від’ємних і - нульових, то тип рівняння називається .

При такій класифікації тип рівняння не змінюється при не виродженій заміні змінних.

Доведення проводиться за схемою :

1. Існує лінійне перетворення таке що , D- діагональна матриця, матриця транспонована до .

2.Власні числа діагональної матриці є діагональними елементами.

3.При перетворенні координат .

4. .

Матриця Т зводиться до того ж самого діагонального виду за допомогою матриці , тому власні числа матриць Т і Т однакові, тип рівняння не зміниться.

4. Зведення до канонічного вигляду диференціальних рівнянь в частинних похідних ІІ-го порядку від двох незалежних змінних.

О. а)Еліптичне рівняння називається канонічним, якщо воно подається так

або

Ознака цього рівняння: змішаної похідної немає і А=С=1;

б)Гіперболічне рівняння називається канонічним, якщо воно подається в одній із двох форм: ,

в) Параболічне рівняння називається канонічним, якщо воно має такий вигляд:

( )

В означеннях а) – в) вираз Ф не містить похідних другого порядку.

Теорема.

Існує невироджене перетворення координат, яке кожне рівняння II-го порядку зводить до канонічного виду.

Доведення.

1) Для доведення твердження вводимо поняття характеристики рівняння.

. (4)

Вираз в дужках не містить похідних другого порядку.

О. Лінія називається характеристикою рівняння (1), якщо функція задовольняє таке диференціальне рівняння I-го порядку

або (5)

Рівняння (5) зводиться до звичайного диференціального рівняння I-го порядку. Дійсно, якщо , , то:

; ; ; ;

На підставі зазначеного і (5) маємо

(6)

Рівняння (6) називається рівнянням характеристик для (4)

Розв’язки цього рівняння:

(7)

2) Якщо рівняння гіперболічне, то рівняння (7) розпадається на два дійсні. Припустимо, що загальні інтеграли цих рівнянь, тоді ці функції приймаємо за нові змінні. В цих змінних рівняння (4) зводиться до канонічного виду бо при такій заміні змінних у рівнянні

коефіцієнти . Дійсно ; оскільки та задовольняють (5), то

Перетворене рівняння ділимо на 2 , і дістаємо канонічне гіперболічне рівняння

3) Якщо рівняння параболічне, то рівняння (7) вироджується в одне

.

Нехай - загальний інтеграл цього рівняння. Покладемо Другу змінну вибираємо довільно, але так щоб якобіан не дорівнював нулю. У нових змінних та параболічне рівняння буде канонічним.

4) Якщо рівняння еліптичне, то рівняння (7) розпадається на два з комплексно-спряженими правими частинами. В цьому випадку інтегруємо одне з них загальний інтеграл диференціального рівняння. За нові змінні приймаємо . Після такої заміни дістаємо канонічне еліптичне рівняння

Дійсно, оскільки початкове рівняння (5) з дійсними коефіцієнтами, то разом з розв’язками будуть: , , беремо перше рівняння. Тоді . Знайдемо коефіцієнти

Якщо підставити у рівняння характеристик, то дістанемо . , бо рівняння буде І-го порядку. Рівняння набуває вигляду

, або .

Зауваження.

Якщо початкове рівняння містить тільки сталі коефіцієнти, то можна звести його до такого вигляду, щоб не було і перших похідних шуканої функції. Для цього вводимо підстановку невідомі числа, підбираємо їх так, щоб перетворене рівняння не містило похідних І-го порядку: Коефіцієнти біля частинних похідних І-го порядку будуть залежати від ; прирівнюємо їх до нуля і знаходимо відповідні значення і .

Згідно означення канонічний вигляд рівняння буде таким:

або

Приклад 6. Звести до канонічного вигляду:

Рівняння лінійне однорідне диференціальне рівняння в частинних похідних другого порядку з двома змінними.

- гіперболічне.

Характеристичне рівняння

Знаходимо дві сім’ї характеристик

Характеристиками є праві і ліві вітки сім’ї парабол

Вершини парабол, які належать осі , не належать характеристикам ;

Заміна

.

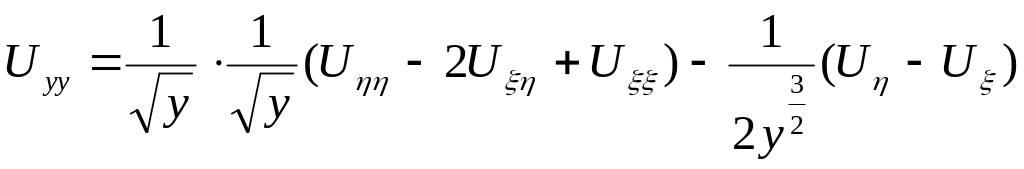
Приклад 7. Звести до канонічного вигляду:

- параболічне.

Заміна

Приклад 8. Звести до канонічного вигляду (приклад 1) якщо . Еліптичне рівняння.

.

Приклад 9. Звести до канонічного вигляду:

– параболічне;

, ;

;

.

~