Тема 1.2. Рівняння гіперболічного типу

1. Рівняння коливання струни.

О. Струною називається нитка яка не чинить опору при згинанні і діє тільки на розтяг.

Будемо розглядати поперечні коливання струни, при таких коливаннях точки струни рухаються в одній площині перпендикулярно до стану рівноваги.

Розглянемо тільки малі коливання – це такі, коливання при яких відхилення точок струни від стану рівноваги значно менше від довжини струни, а сама струна під час коливань досить полога.

Якщо на струну не діють ніякі зовнішні впливи, то коливання називаються вільні. Таким чином, розглядаємо вільні, поперечні, і малі.

Рівняння вільних коливань струни можна подати у вигляді:

(1) де - координати точки струни,

час,

швидкість точки, стала.

Розглянемо нескінчену струну

.

2. Задача Коші для нескінченної струни.

Так називається задача: Знайти розв’язок рівняння.

,

який задовольняє початкові умови :

початкова форма струни; початкова швидкість.

Задачу Коші можна сформулювати так:

Розв’язати(1),якщо відомі початкова форма і початкова швидкість струни.

Розв’язання задачі Коші:

1. Зводимо рівняння до канонічного виду

- (гіперболічне)

2. Рівняння характеристик:

,

(**)

3. 

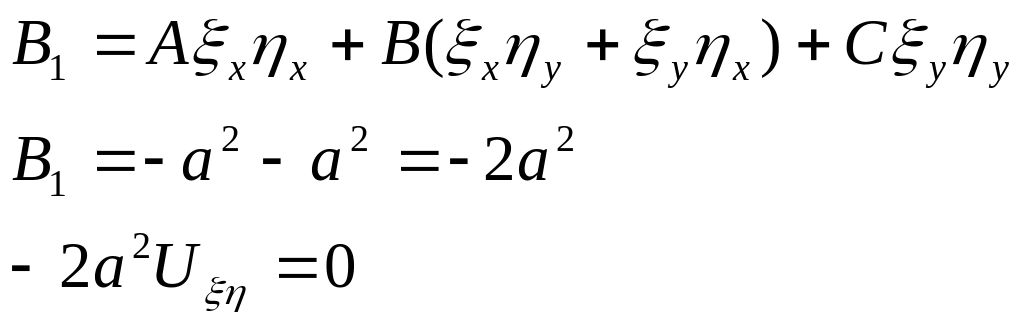
- від не залежить, тоді залежить тільки від .

- загальний розв’язок (**).

Рівняння містить дві довільні функції та . Добираємо ці функції так, щоб виконувались початкові умови.

Інтегруємо друге рівняння і розв’язуємо систему рівнянь відносно та .

– Розв’язок задачі Коші для вільної нескінченної струни.

(формула Даламбера)

Зауваження. Результуюча коливання струни є результатом накладання коливань, викликаних початковою формою і початковими швидкостями окремо.

3. Вільні коливання напівнескінченної струни.

О.Струна з одним закріпленим кінцем називається напівнескінченною. Домовимось вважати що струна має лівий кінець, який поміщений в початок координат. Кінець може бути вільним, а може бути закріпленим, розглядаємо закріплений кінець.

Задача.

Знайти розв’язок рівняння,

(1)

який задовольняє умови:

(2)

(3)

(4)

Умови (2) і (3) називаються початковими, а умова (4) називається межовою. Початкові і межові умови разом називаються крайовими , через це задача називається крайовою.

Теорема.

Розв’язок вказаної крайової задачі подається формулою:

Доведення.

1. Зводимо диференціальне рівняння до канонічного виду

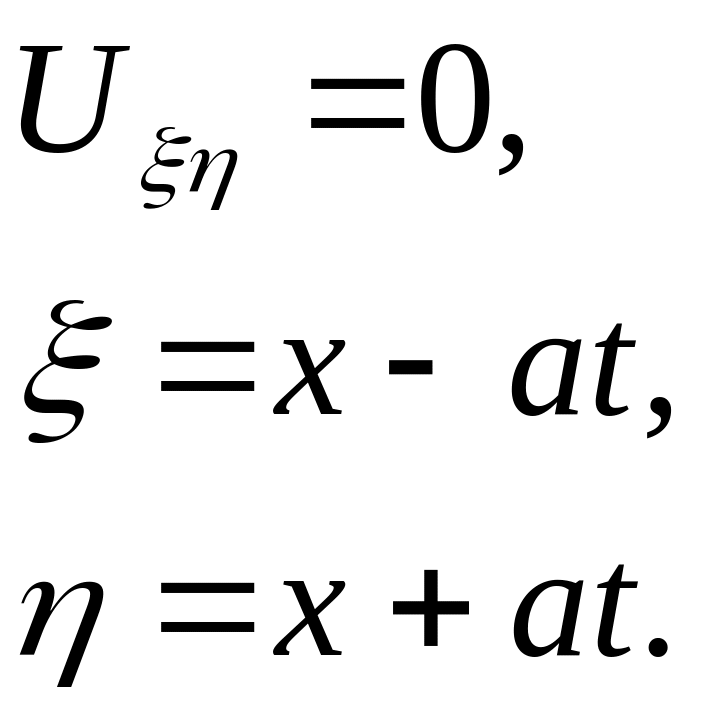
2. Знаходимо загальний розв’язок рівняння 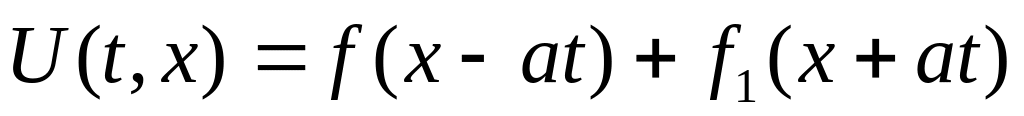, де і - довільні функції.

3. Знаходимо залежність між і на основі крайових умов , .

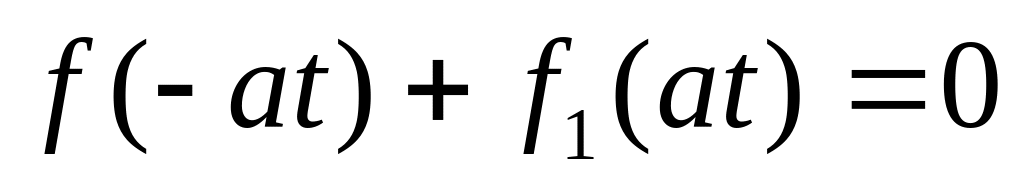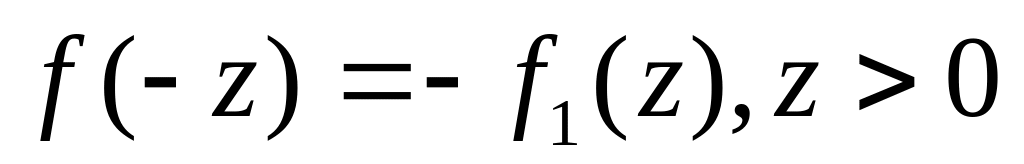4. Знаходимо та з початкових умов.

Після використання процедури описаної в попередній задачі дістанемо:

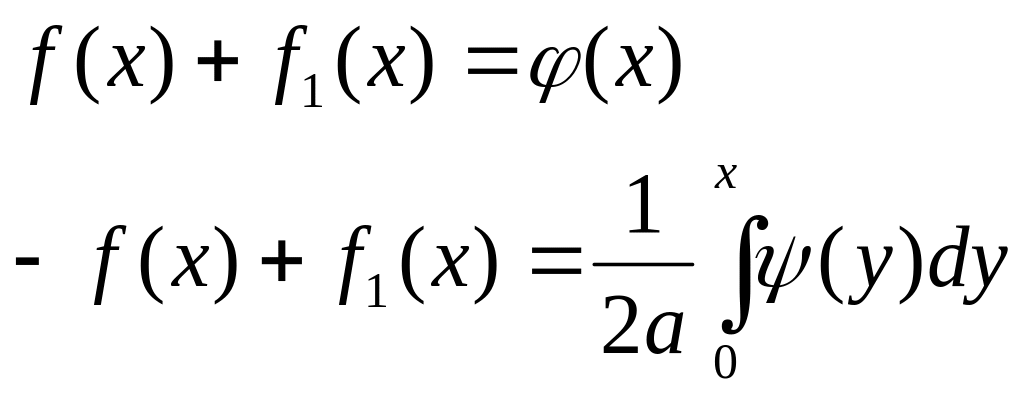(5)

Після додавання в (5) дістанемо:

. Замінивши на , маємо: (6)

Після віднімання у (5) дістанемо:

. Розглянемо два випадки:

а)

(формула Даламбера).

б) , заміняємо

Зауваження 1.

Ми довели що при умові існування розв’язку він подається відповідними формулами і тому єдиний. Потрібно переконатись, що одержані функції є розв’язками рівняння, які задовольняють задані крайові умови. При цьому потрібно використати правило диференціювання інтеграла залежного від параметру.

, .

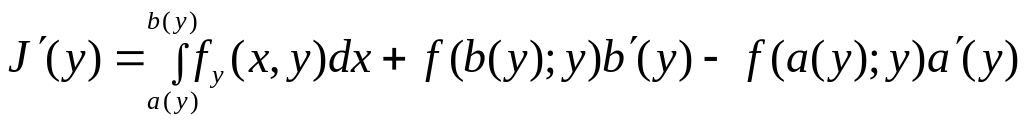Зауваження 2.

Рівність, записану в теоремі, можна подати строчкою у формі, аналогічній формулі Даламбера. Для цього потрібно функції і продовжити непарним способом на всю вісь.

аналогічно