8.Одномірне рівняння теплопровідності. Задача Коші.

Нехай тонкий теплопровідний стержень розміщений вздовж осі , так що температуру в кожному її перерізі можна вважати функцією тільки абсциси і часу Бічна поверхня стержня теплоізольована.

Задача Коші для однорідного рівняння теплопровідності:

Знайти розв’язок рівняння , (1)

яке задовольняє умову (2)

якщо

З адача Коші описує температурний режим у нескінченному стержні із заданим початковим температурним режимом

U(t,x)- температура стержня в момент часу t в точці х.

0 х

Задача без межових умов називається задачею Коші. Будемо вважати, що поверхня стержня теплоізольована. Це рівняння лінійне однорідне:

Розв’язуємо задачу методом Фур’є.

1. Подаємо шукану функцію у вигляді добутку відокремлених змінних.

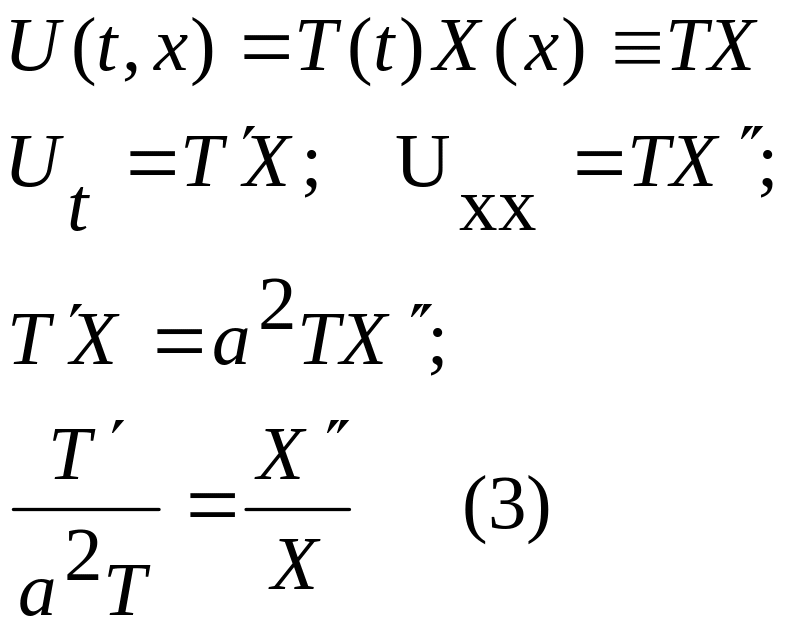
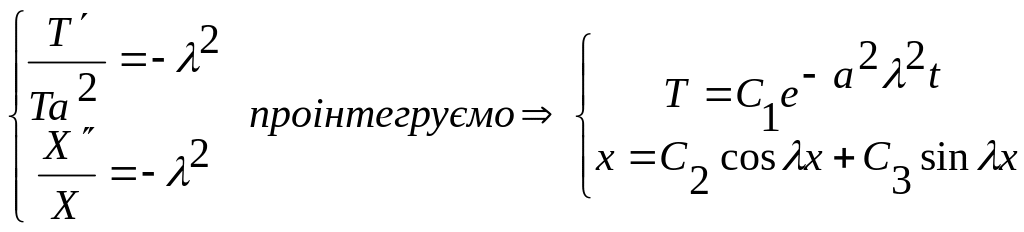
2. Підставимо

Внаслідок відсутності межових умов (стержень нескінчений) може набувати значення від до . Тому замість підсумування (яке використовується в методі Фур’є, при накладанні стоячих хвиль, що мають дискретні власні значення) ми повинні накладати розв’язки неперервно, тобто утворювати розв’язок рівняння (1) інтегруванням по в межах від до .

(*)

3. Використовуючи початкові умови знаходимо коефіцієнти

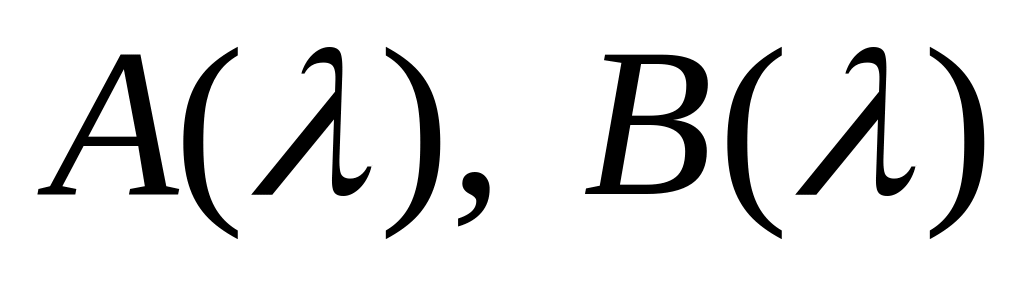
- інтеграл Фур’є для функції . Відомо, що коефіцієнти подаються формулами:

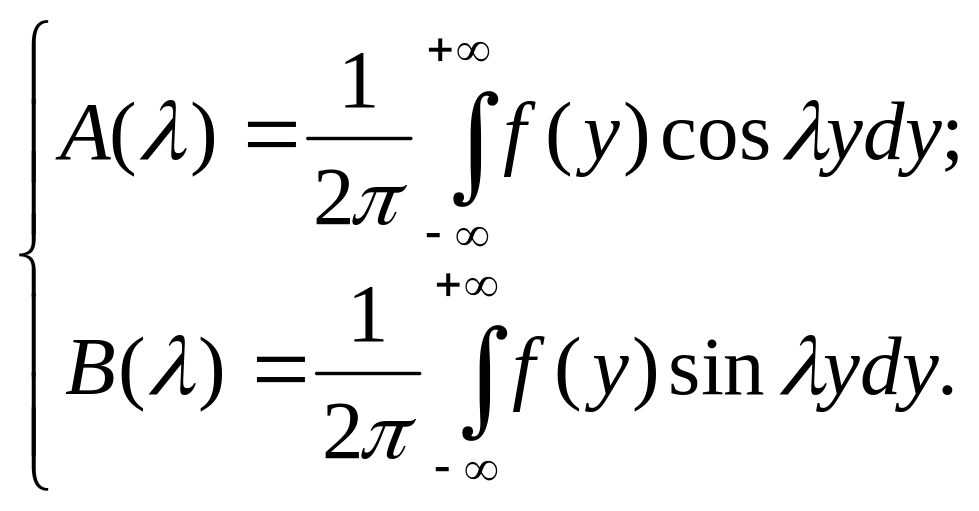
Висновок.

Розв’язок задачі Коші подається інтегралом (*), коефіцієнти подаються формулами (**).

Перетворення інтеграла (*).

Якщо у рівність(*) підставити значення і , то дістанемо

Для фізичного тлумачення цього розв’язку змінюємо порядок інтегрування. Дістанемо

Обчислюємо внутрішній інтеграл:

1) ;

Дістаємо

Розглянемо інтеграл:

У показнику степеня виділяємо повний квадрат:

Дістаємо

В иконуємо заміну змінних

-А ⁰ А

В останньому інтегралі можна вважати дійсним. Пояснюється так: утворимо прямокутник, інтеграл по замкненому контуру (на малюнку) дорівнює нулю, отже інтеграл по верхньому відрізку дорівнює інтегралу по нижньому.

Якщо спрямувати А до то дістанемо те, що вимагалось. Враховуючи, що останній інтеграл дорівнює . Дістанемо

,

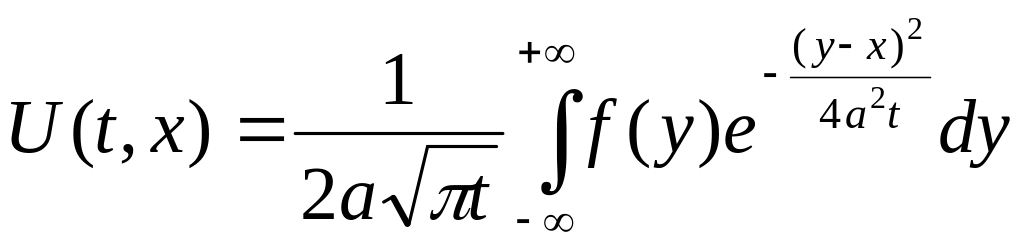Остання формула подає температурний режим у нескінченому стержні при заданому початковому розподілі температур.

Зауваження. Щоб переконатись, що функція є розв’язком вказаної задачі Коші, потрібно довести, що вона задовольняє рівняння (1) і початкову умову(2).

(А) 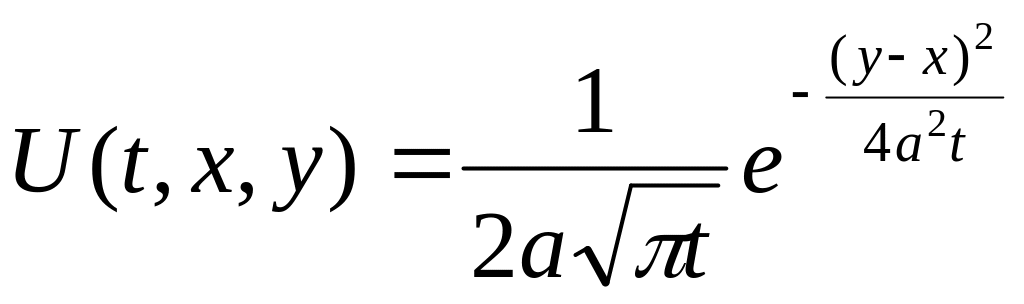- задовольняє рівняння(1), тому називається фундаментальним розв’язком задачі Коші .

Можна довести, що функція (а) задовольняє одномірне рівняння теплопровідності, через це називається фундаментальним розв’язком рівняння теплопровідності.

З’ясувати поведінку цієї функції у випадках:

а) t – фіксована;

б) x – фіксована.

1. Фізичний імпульс. Так називається розподіл температури в нескінченному стержні, якщо початкова температура 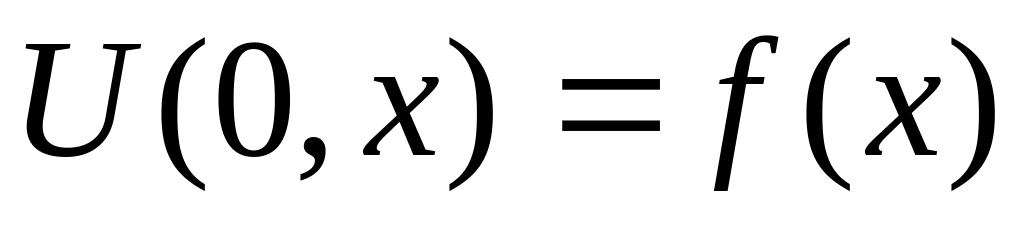подана на рисунку.

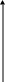
0

. Площа прямокутника -

Знаходимо температурний режим при функції ,

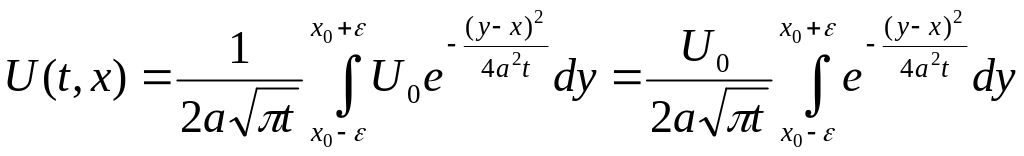. Застосовуємо теорему про середнє .
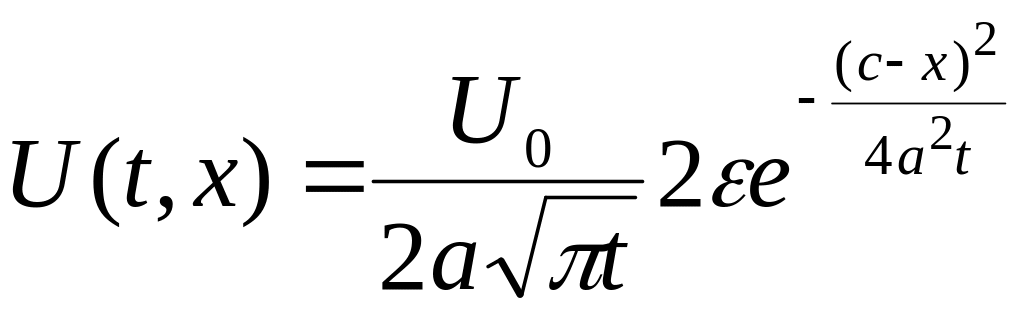