6.Рівняння Бесселя. Функції Бесселя.

О. Рівнянням Бесселя називається лінійне диференційне, однорідне рівняння II – го порядку для р- дійсне число.

Розв’язок шукаємо у вигляді узагальненого степеневого ряду.

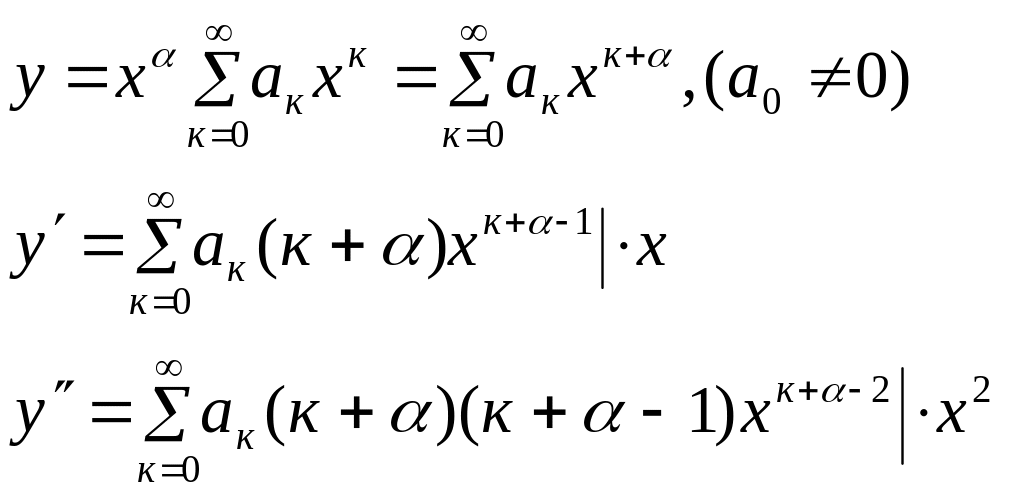
Звідси слідує що коефіцієнт при кожному степені , повинен дорівнювати нулю.

При

При

При

При

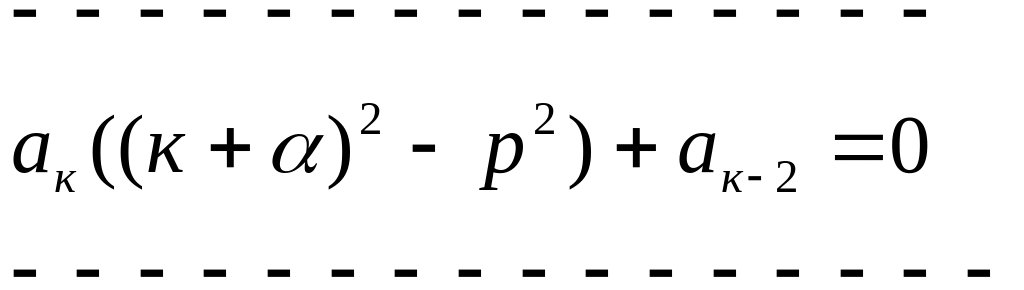
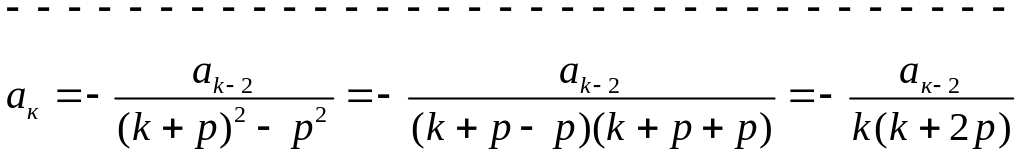
Коефіцієнти з непарними індексами дорівнюють 0.

довільне

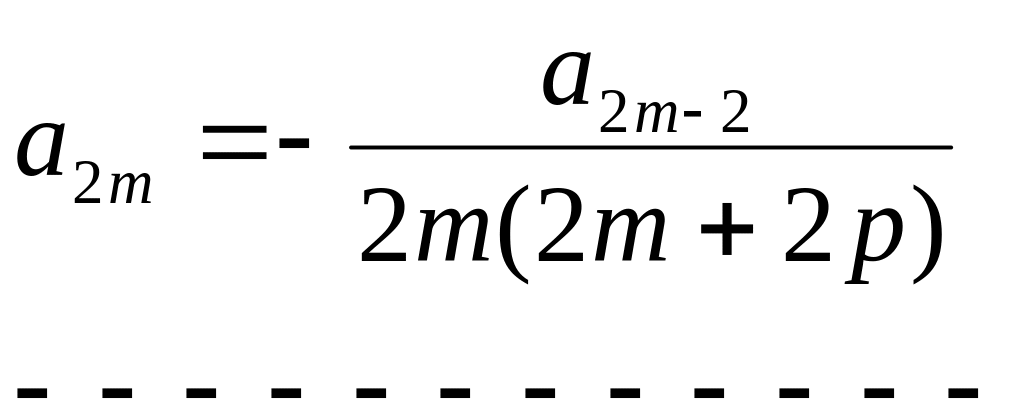
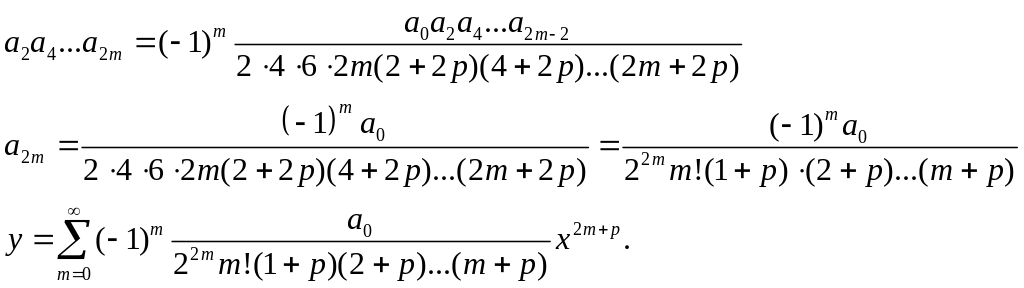
Розв’язок рівняння подається у вигляді -

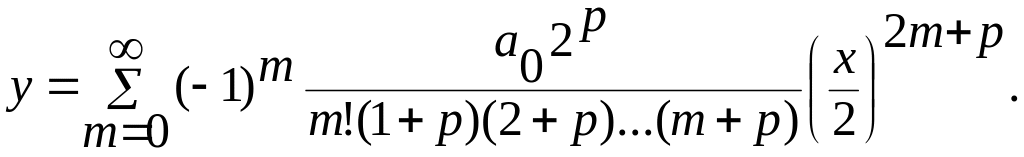
2.Подача коефіцієнтів через г-функцію.

1). _{Г-функцією називається такий інтеграл}

2). Має місце така рівність

.

Зокрема, ,

.

Якщо ( простий полюс )

Г-функцію можна продовжити на всю комплексну площину. Числа 0, -1,-2,...є прості полюси.

3) Розв’язок рівняння Бесселя можна подати у такому вигляді

Оскільки - довільне число, то беремо його таким, щоб було

У цьому випадку

Називається функцією Бесселя першого роду порядку .

Якщо не є цілим, то рівняння Бесселя має два лінійно незалежні розв’язки:

Якщо – натуральне число, то можна довести, що

Другий лінійно незалежний розв’язок необмежений в точці х=0. Це так звана функція Неймана.

Вивчення бесселевої функції першого роду , виходячи з наведеного розкладу в степеневий ряд, являє деякі математичні утруднення. Але ці функції, в силу їх важливості, для застосувань, добре вивчені і протабульовані (тобто існують детальні таблиці їх значень) для великих

мало відрізняється від або точніше

де якщо

Функція

1) є розв’язком рівняння (у рівнянні Бесселя );

2)

3) ;

4) Функція має безліч нулів .

Відстань між сусідніми нулями з великими індексами приблизно дорівнює .

y

1

2.4 5.5 8.7 x

5) (властивість ортогональності)

Амплітуда цієї хвилі прямує до 0 зі швидкістю . Друга лінійно незалежна функція, що є розв’язком рівняння Бесселя, буде необмеженою в точці x=0. Вона називається функцією Неймана N .

Загальний розв’язок рівняння Бесселя є лінійна комбінація . де - обмежена, а - необмежена.

Приклад. Довести, що

,де

використовуємо той факт, що , маємо

, що й треба було довести.

Приклад. Перевірити чи виконується рівність:

Розв’язання:

Підставляємо отримані результати в умову:

Таким чином рівність правильна.

7. Коливання круглої мембрани.

Постановка задачі:

Розв’язати двомірне хвильове рівняння ,

(1)

яке задовольняє такі умови:

r

r- полярний радіус;

- полярний кут;

- координати.

Найбільший інтерес являє випадок, коли кругла мембрана коливається, зберігаючи форму поверхні обертання навколо осі, що проходить через центр мембрани і перпендикулярна їй, тобто коли не залежить від . Такі коливання називаються осесиметричними. Для осесиметричних коливань початкові умови (2) і (3).

1. Подаємо рівняння (1) в полярних координатах

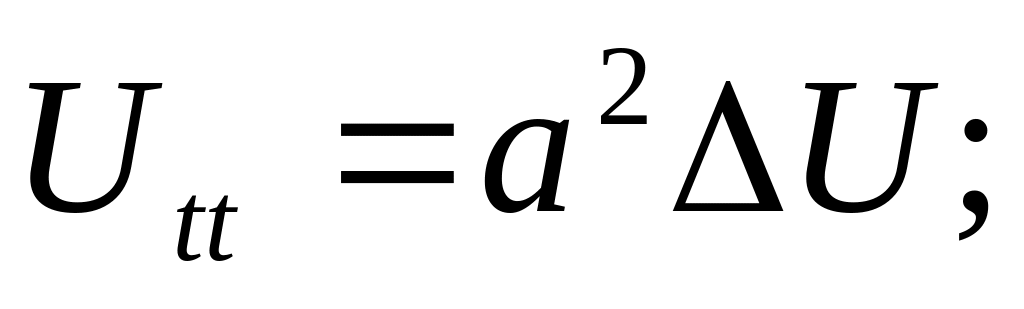
не залежить від

2. Застосовуємо метод відокремлення змінних (метод Фур’є).

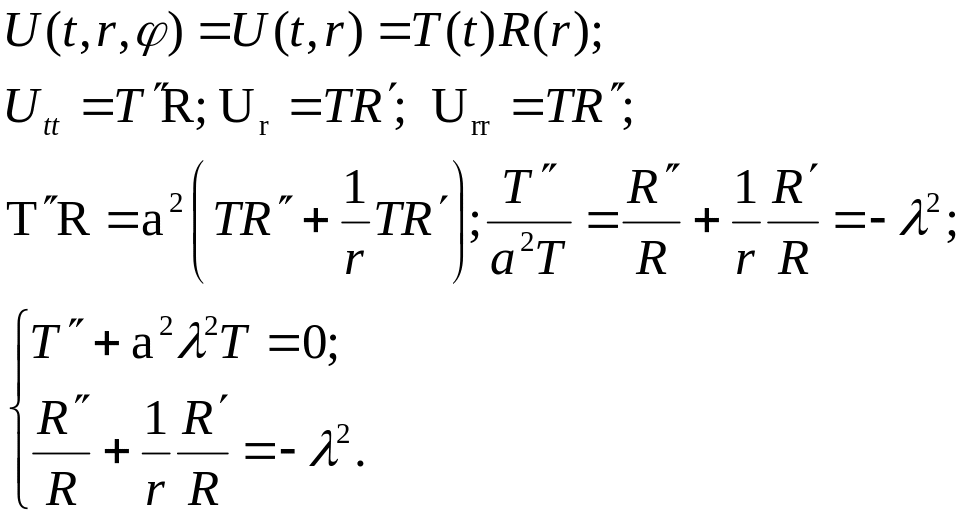
3. Розв’язуємо кожне з одержаних диференціальних рівнянь.

а)

б)

; .

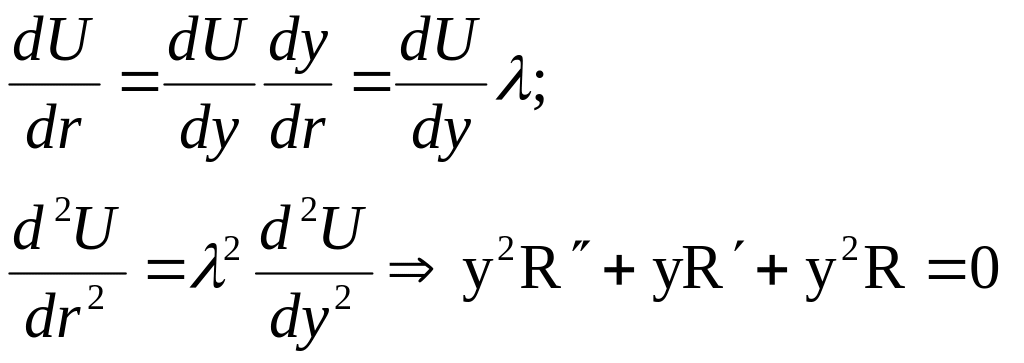
• рівняння Бесселя для р=0

Розв’язком цього рівняння, як відомо, є ( - функція Бесселя першого роду нульового порядку.

.

4)

5. Використаємо межові умови і знаходимо параметр - власні числа.

- числа є нулями для функції Бесселя з нульовим індексом.

. Існує безліч власних значень, (спектр власних значень).

Висновок.

6. Подаємо розв’язок задачі у вигляді ряду: .

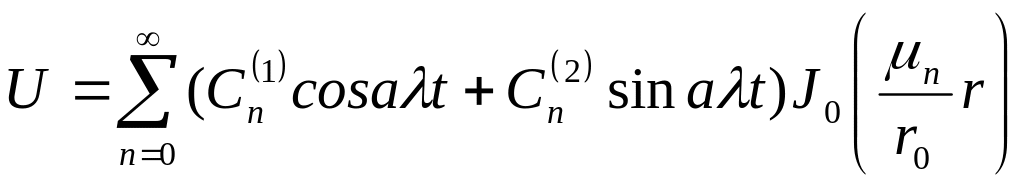6. Використовуємо початкові умови і знаходимо С і С . 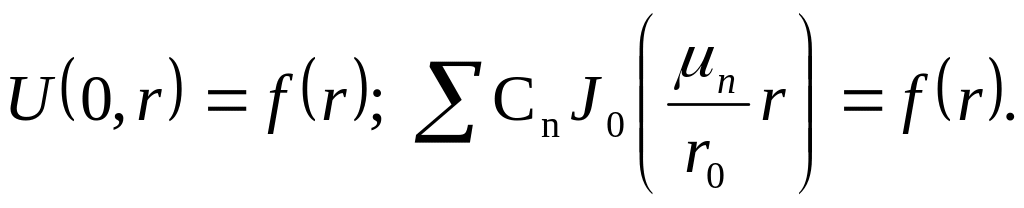Функції Бесселя мають властивість ортогональності з вагою х:

, ,

- функція Бесселя першого роду -го порядку.

Коефіцієнти і знаходяться по формулі

, ,

, .

На основі цієї властивості визначаються коефіцієнти, для цього ліву і праву частину помножимо на , інтегруємо на проміжку [0,1] по .

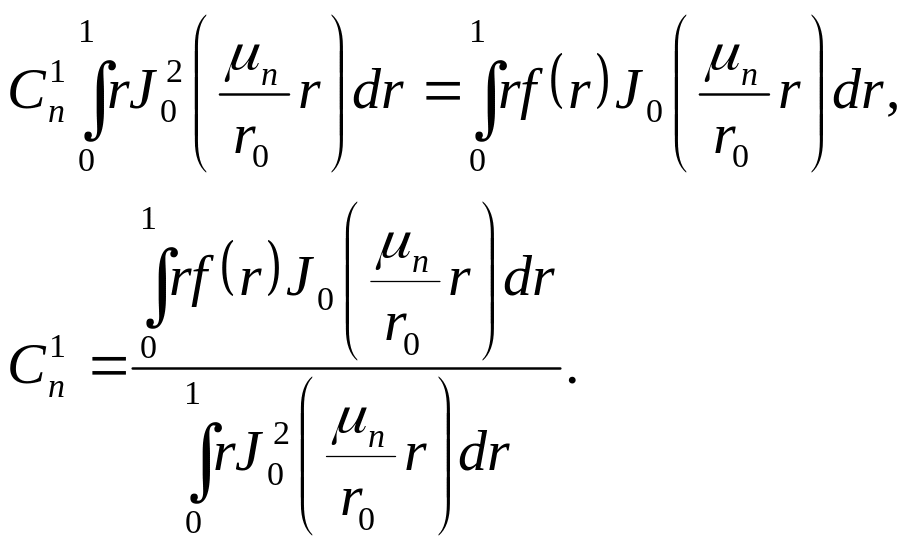
- є коефіцієнтами Фур’є для функції за функціями Бесселя нульового порядку. Аналогічно знаходимо коефіцієнти .

С - є коефіцієнтами Фур’є для функції F за функціями Бесселя нульового порядку.

Підсумок.

Для розв’язування задачі про коливання круглої мембрани необхідне введення нових спеціальних функцій, а саме функцій Бесселя, і використання їх ортогональності з вагою x. Ці функції ще називаються циліндричними.