5.1 Крайова задача.

Знайти розв’язок рівняння

якщо:

Задані початкові умови

- початкова форма мембрани;

- початкова швидкість точок мембрани;

- межові умови. Край мембрани закінчений

Розв’язання (метод відокремлення змінних, метод Фур’є)

1)

2) ; поділимо на , отримаємо

(при , коливань немає), це рівняння розпадається на два:

і .

3) Використаємо крайові умові для знаходження .

а) ОА: у=0; ;

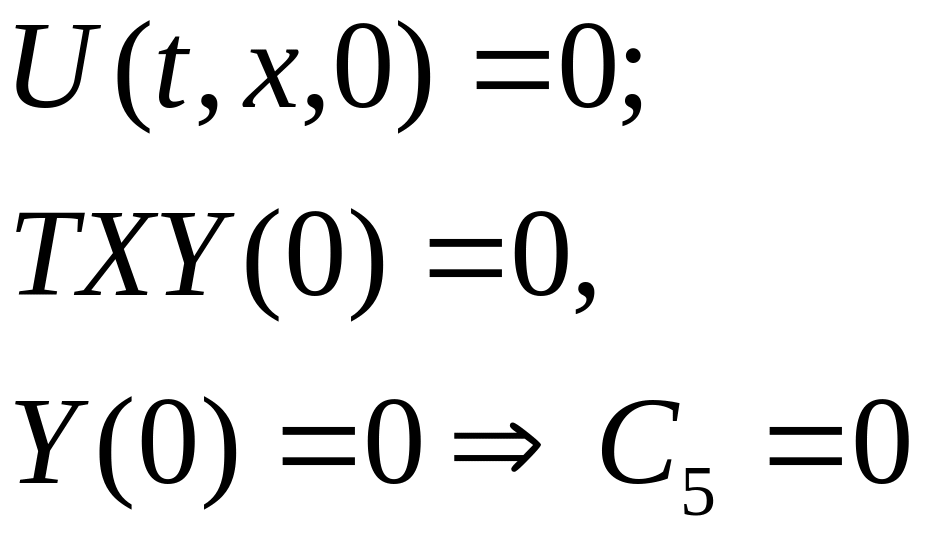
б) СВ: ;

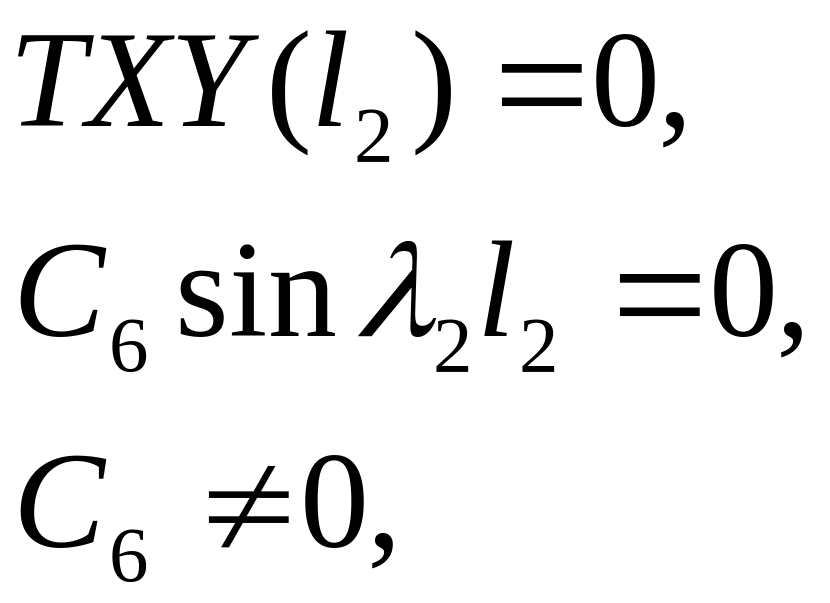
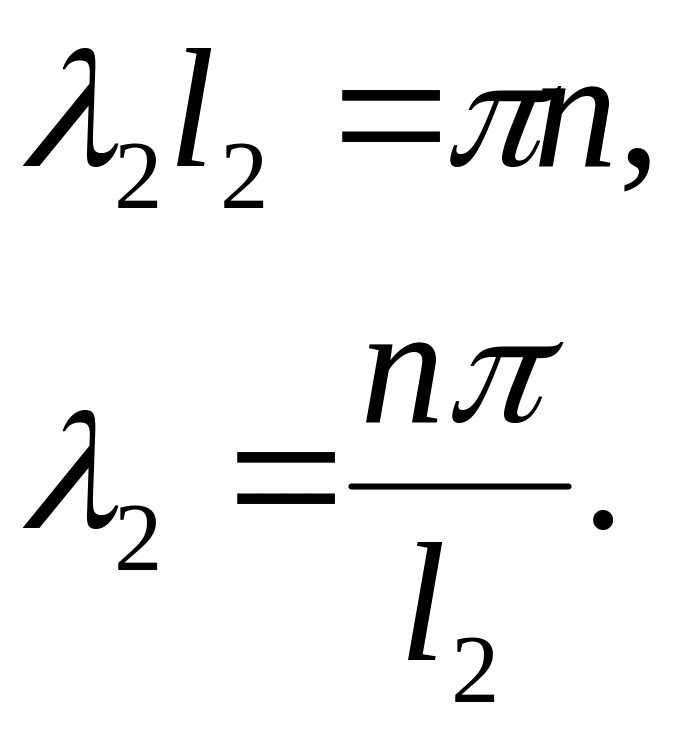
в)

г)

(*)

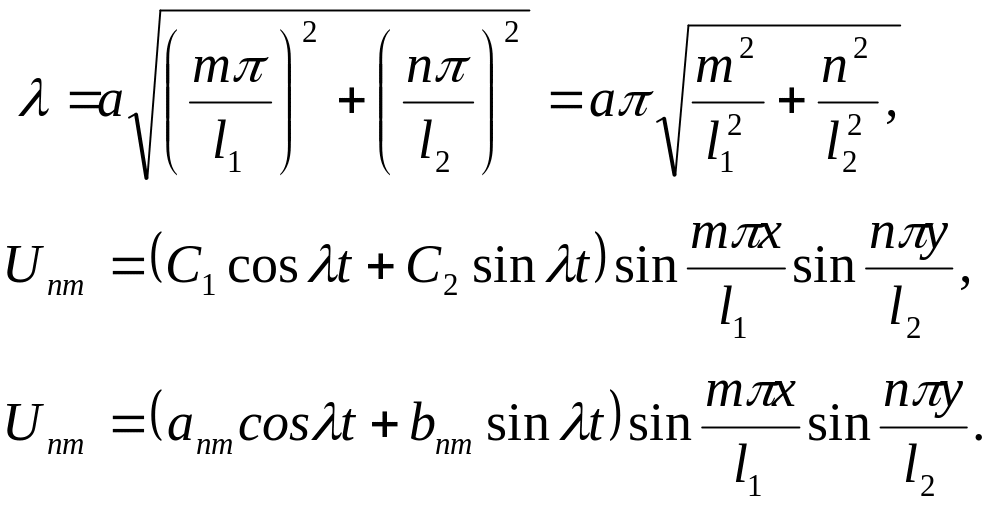
(1)

Оскільки рівняння лінійне, однорідне, то лінійна комбінація за двома індексами буде розв’язком рівнянь.

.

4) Використовуємо початкові умови і знаходимо коефіцієнти та

а)

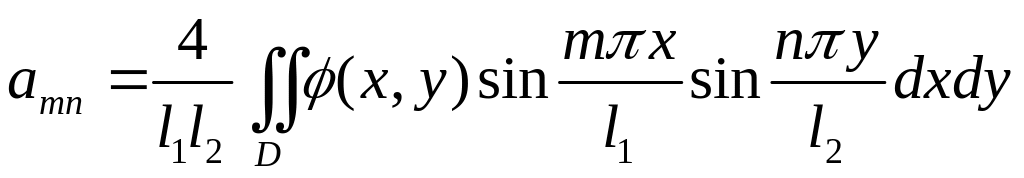. (3)

Аналогічно, про диференціювавши по t, знаходимо

. (4)

Висновок:

Розв’язок крайової задачі подається у вигляді подвійного ряду (2) за синусами, де коефіцієнти знаходяться за формулами (3), (4), а - за формулою ( ).

Фізична інтерпретація розв’язку.

(*)

Власні функції утворюють ортогональну систему власних функцій прямокутної мембрани.

Частоти , що визначаються формулою (*), називаються власними

частотами прямокутної мембрани, а коливання (1) - її власними

коливаннями.

Коливання, які відповідають власним частотам, називаються обертонами

Розглянемо випадок тоді

Лінії, точки в яких не коливаються, називаються вузловими лініями.

З’ясуємо, де які лінії вузлів,

Вузлові лінії будуть:

а) паралельні координатним осям

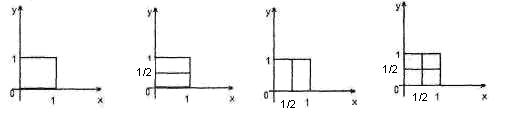
б) мати складну форму

Власні коливання являють собою стоячу хвилю для прямокутної мембрани. Кожна точка х,у здійснює гармонічне коливання з частотою

і амплітудою причому всі точки мембрани одночасово досягають свого максимального відхилення в ту чи іншу сторону. Наприклад, форма мембрани при коливаннях в

момент коли точки досягають свого максимального відхилення вгору

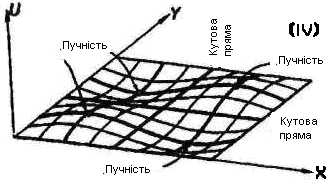
зображено на рис.1.

Точки, в яких мембрана відхиляється максимально вгору (вниз),

називаються пучностями.

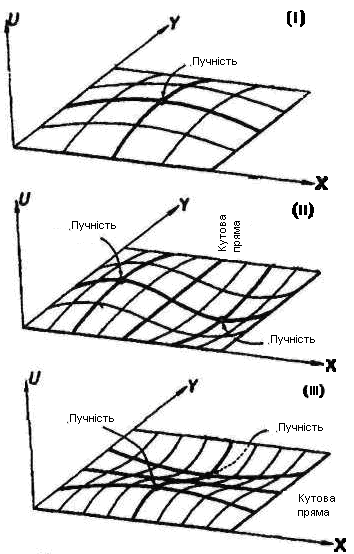
На малюнку зображено стоячі хвилі в той момент, коли всі її

точки досягають найбільшого відхилення.

Наступні стоячі хвилі мають більш складний вигляд.

У випадку кратних власних значень вузлові лінії часто називають

Фігурами Лісажу.

Приклад.

Розглянемо коливання квадратної мембрани (m=l), всім точкам якої (не рахуючи, звичайно, точок межі) надаються однакові початкові швидкості . Тоді будемо мати початкові умови: тобто

За формулою 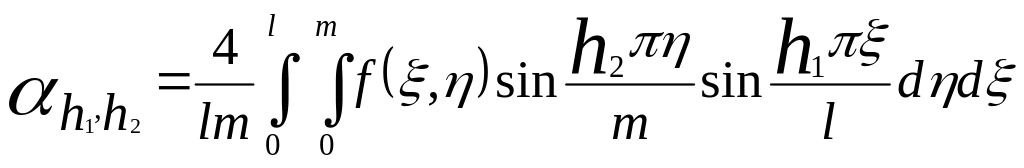буде , а по формулі :

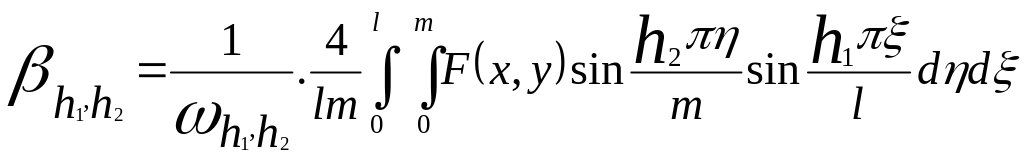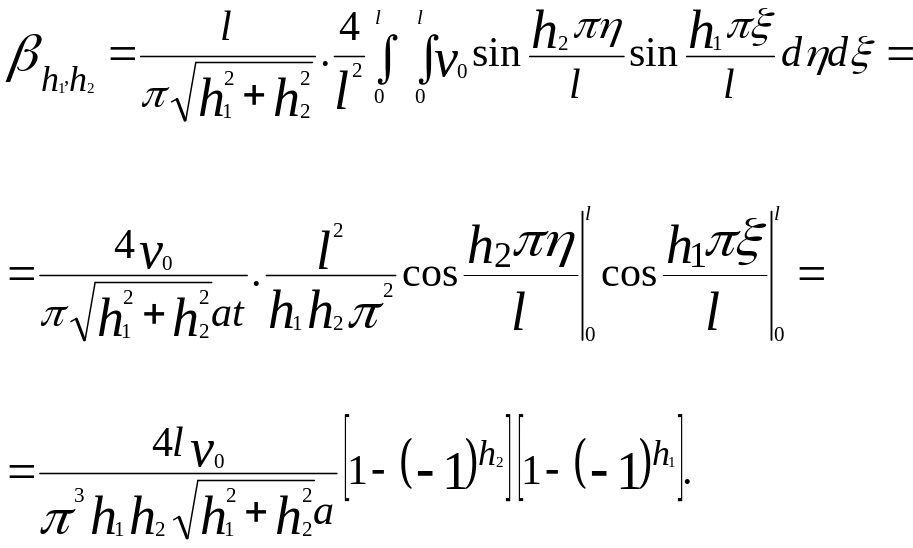
Якщо хоч один з індексів чи - парний, то цей вираз рівний нулю. Тому покладемо , , , і знайдемо, що відмінні від нуля коефіцієнти

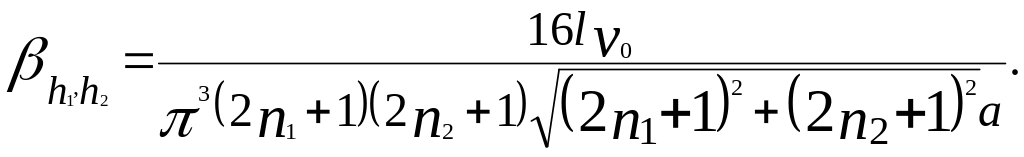
Таким чином,