4. Вільні коливання скінченої струни.

Вважаємо що струна має довжину і закріплена на кінцях. Лівий кінець в початку координат.

Задача.

Знайти розв’язок рівняння,

який задовольняє такі крайові умови:

Метод розв’язання.

Метод Фур’є (метод відокремлення змінних).

1) Розв’язок шукаємо у формі добутку функцій від x і t:

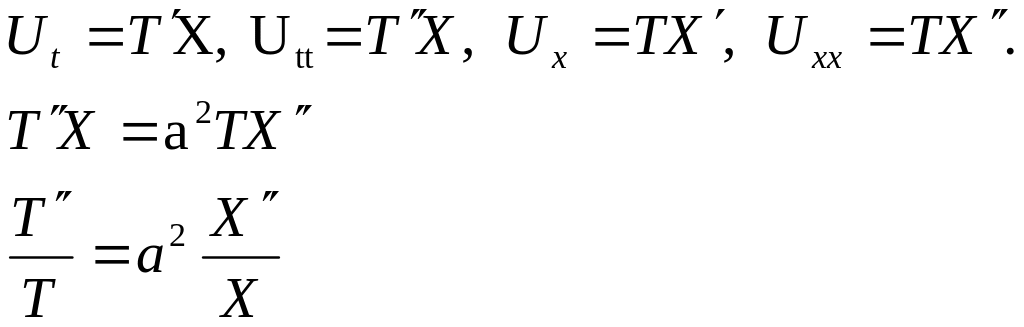
Ліва частина залежить тільки від , а права тільки від . Вони рівні між собою. Тому кожна частина є сталою:

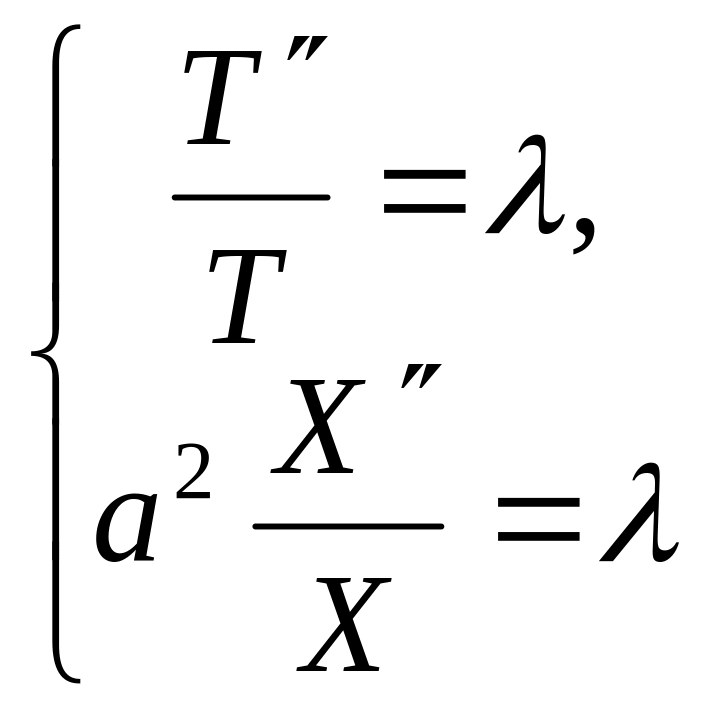
Можливі випадки:

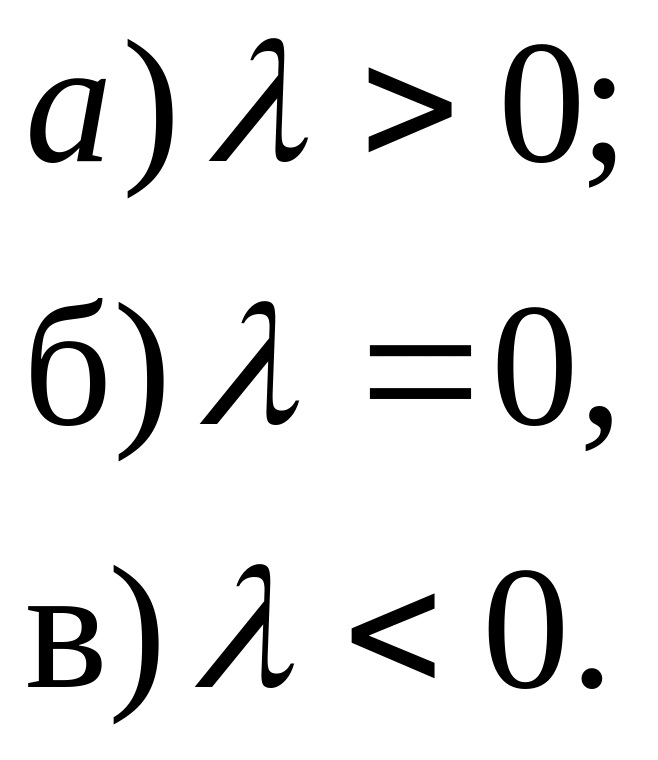
Неважко довести, що у випадках а), б) і коливань немає. Розглянемо в) покладемо , тоді

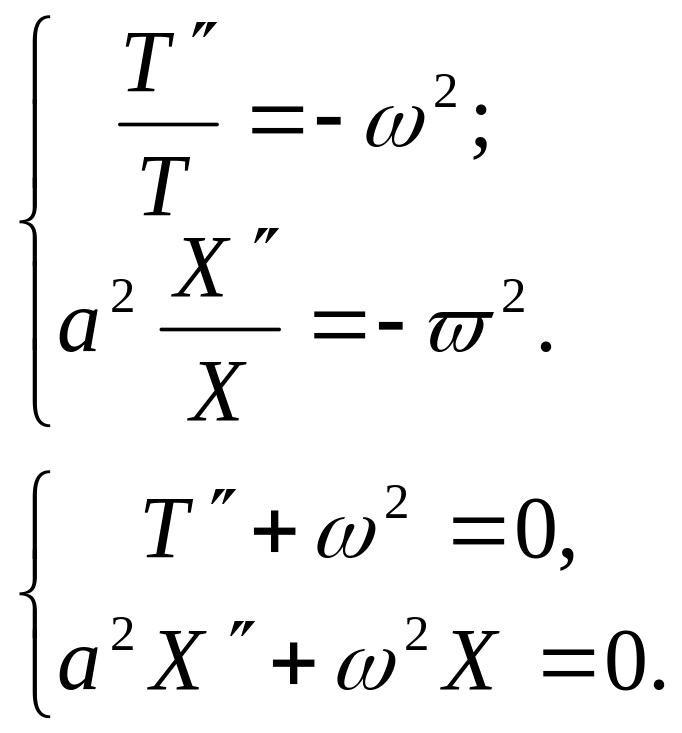
Дістали два лінійні диференціальні рівняння 2-го порядку з сталими коефіцієнтами.

а) - характеристичне рівняння для першого;

б) - характеристичне рівняння для другого;

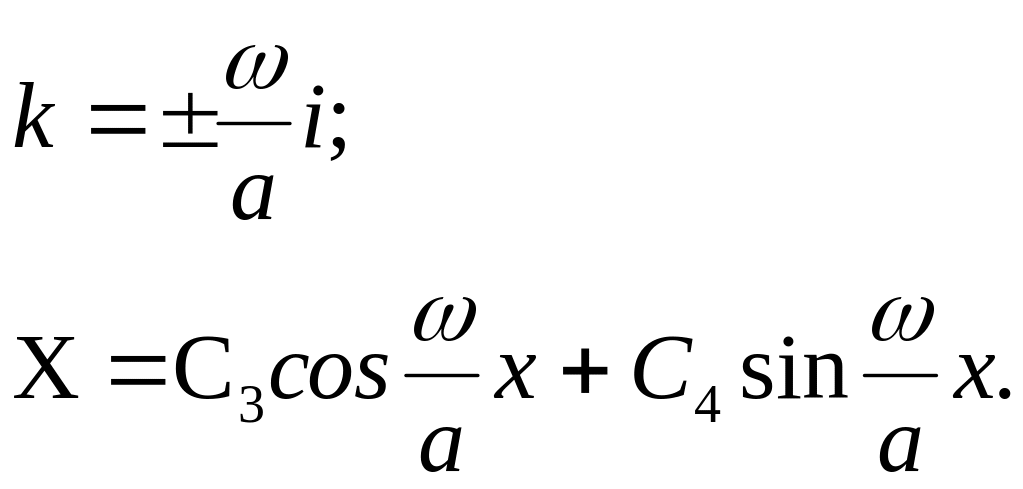
Довільні сталі знаходимо з початкових умов, а із крайових.

2) Спочатку використовуємо крайові умови.

а)

(коливань немає).

Якщо тоді

б) Розглянемо другу умову:

таким чином, для знаходження дістали рівняння:

(коливань немає)

або підставляємо в та

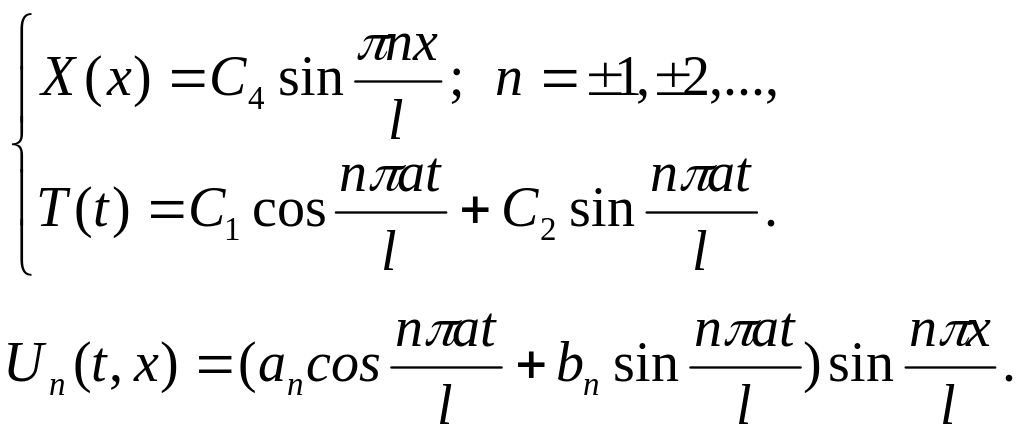
Внаслідок довільності коефіцієнтів в останній формулі вважаємо n=1,2,3...

Оскільки рівняння однорідне, то лінійна комбінація одержаних розв’язків є також розв’язком. У нашому випадку дістаємо ряд.

3) Початкові умови :

а)

Остання рівність означає, що є коефіцієнтами Фур’є функції , розкладеної в ряд за синусами, тому

б)

Ця рівність означає, що числа є коефіцієнтами Фур’є для функції , розкладеної на за синусами, тому

Звідси

Висновок.

Розв’язок даної крайової задачі подається у вигляді ряду:

Коефіцієнти якого знаходимо за формулами

5. Вільні коливання прямокутної мембрани.

Основні поняття

О.1. Мембраною називається матеріальна пластина яка не чинить опору згинанню і діє тільки на розтяг.

О.2. Функції і називаються ортогональними в області D, якщо .

О.3. Інтеграл від квадрата функції по області D, називається квадратом норми функції .

Функція називається нормованою, якщо її норма дорівнює 1.

О.4. Система функцій (*) називається ортогональною в області D , якщо кожні дві з них ортогональні в області D.

О.5. Система називається нормованою, якщо кожна функція нормована.

О.6. Система називається ортонормованою, якщо вона ортогональна і нормована.

О.7. Функція називається періодичною:

- по змінній x, якщо ;

– по змінній y, якщо .

О.8.Функція називається періодичною по обох змінних , якщо .

Традиційно: .

О.9. Нехай функція задана в прямокутнику із сторонами і в області : функція f продовжена в область непарним способом ; аналогічно продовжимо функцію f непарним способом в область .

Подвійним рядом Фур’є функції за системою називається ряд - , де .

y

l

-l l x

-l

Зауваження.

Якщо функція задана лише в області D і її продовжити на всю область D непарним способом, то .

y

C B

l

l x

0 A

Можна довести, що вільні коливання прямокутної мембрани подаються рівнянням: