5.2. Узагальнення балансової задачі.

Повні витрати праці та капіталовкладень

Розглянемо економічну систему, в якій крім виробничих витрат додаються ще витрати праці та капіталовкладень по кожній галузі. Ці витрати увійдуть до таблиці міжгалузевого балансу як додаткові n+1 – й та n+2 – й рядки. При моделюванні даної економічної системи можуть бути розглянуті також інші види витрат.

Позначимо витрати праці в j-й галузі через , витрати капіталовкладень – через (j= 1, 2,…, n). Тоді коефіцієнти прямих витрат праці і капіталовкладень будуть визначати витрати відповідного ресурсу на одиницю продукції, що випускається j-ю галуззю. При обчисленні цих коефіцієнтів використовуються ті ж самі співвідношення, за якими визначалися коефіцієнти прямих витрат , тобто маємо формули:

; . (2.1)

Залучивши коефіцієнти , в структурну матрицю (тобто дописавши їх до таблиці міжгалузевого балансу у вигляді додаткових рядків), отримаємо розширену матрицю коефіцієнтів прямих витрат:

Додаткові

рядки

Основна частина матриці

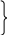
Слід зазначити, що при розв'язанні системи балансових рівнянь, як і раніше, використовується лише основна частина матриці, тобто структурна матриця A. Але при розрахунку на наступний запланований період витрат праці і капіталовкладень, необхідних для випуску даного кінцевого продукту, приймають участь також додаткові рядки.

Визначимо сумарні витрати праці, що пов'язані з виробництвом одиниці кінцевого продукту будь-якої галузі.

Так, нехай, виробляється одиниця кінцевого продукту 1-ої галузі, тобто

.

Для цього потрібен валовий випуск продукції:

.

Враховуючи, що за змістом коефіцієнти прямих витрат праці – це витрати на виробництво одиниці продукції k-ої галузі, а величини характеризують, скільки мають випустити продукції відповідно в кожній галузі при створенні одиниці кінцевого продукту 1-ої галузі. Тоді матимемо: витрати праці безпосередньо в 1-й галузі – , у 2-й галузі – тощо, нарешті, в n-й галузі – .

Сумарні витрати праці, які пов'язані з виробництвом одиниці кінцевого продукту 1–ої галузі, складають

,

тобто дорівнюють скалярному добутку (n+1) – го рядка розширеної матриці (позначимо його ), на перший стовпець матриці S, а саме, на . Аналогічно отримаємо сумарні витрати праці, які необхідні для виробництва одиниці кінцевого продукту k-ої галузі, складають

. (2.2)

Ці величини називають коефіцієнтами повних витрат праці.

Повторюючи всі ці міркування щодо витрат капіталовкладень, отримаємо аналогічні формули розрахунку коефіцієнтів повних витрат капіталовкладень:

. (2.3)

Тепер можна доповнити матрицю S двома рядками, що складаються з елементів і , та утворити розширену матрицю коефіцієнтів повних витрат S':

Матриця

коефіцієнтів

повних

внутрішніх

виробничих

витрат

Додаткові

рядки

(2.4)

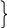
Користуючись цією матрицею, можна розрахувати при будь-якому заданому асортиментному векторі не тільки необхідний валовий випуск продукції (для чого використовується матриця S), але і необхідні сумарні витрати праці , капіталовкладень тощо, які забезпечують випуск даної кінцевої продукції .

Сумарні витрати праці і капіталовкладень, необхідних для забезпечення асортиментного вектора кінцевої продукції , дорівнюють скалярному добутку відповідного додаткового рядка матриці на вектор , тобто

; . (2.5)

Поєднуючи формулу (1.3), з формулами (2.5), отримаємо наступну компактну формулу

. (2.6)

Задача 2. Розглянемо економічну систему, у якій виділені чотири сектори: три виробляючі сектори (сільське господарство, промисловість, транспорт) і домашні господарства як сектор кінцевого попиту. В цій системі крім виробничих витрат будемо враховувати витрати праці і капіталовкладень по кожній галузі. Структура економіки наведена у таблиці міжгалузевого балансу на рис. 3.13. (обсяги визначені в тис. грн., затрати праці – в тис. люд.-годин, капіталовкладення – тис. грн.).

	Промисловість	Сільське господарство	Транспорт	Домашні господарства (сектор кінцевого попиту)	Загальний випуск
Промисловість	10	30	180	100	320
Сільське господарство	16	50	120	60	246
Транспорт	14	15	140	80	249
Витрати праці	8	45	90
Витрати капіталовкладень	100	240	360

Рис. 3.13. Міжгалузевий баланс економічної системи

Завдання до задачі 2.

1. Розрахувати при заданому асортиментному векторі такі показники плану, як валова продукція кожної галузі , сумарні витрати праці і капіталовкладень, що забезпечують випуск даної кінцевої продукції .

2. Визначити зміну вектор – плану , а також зміну сумарних витрат праці і капіталовкладень, яка буде потрібна для збільшення кінцевого випуску виробів 1-ої галузі на 10 одиниць, 2-ої галузі на 30 одиниць, 3-ої галузі на 20 одиниць, тобто кінцевий вектор випуску буде мати вид: .

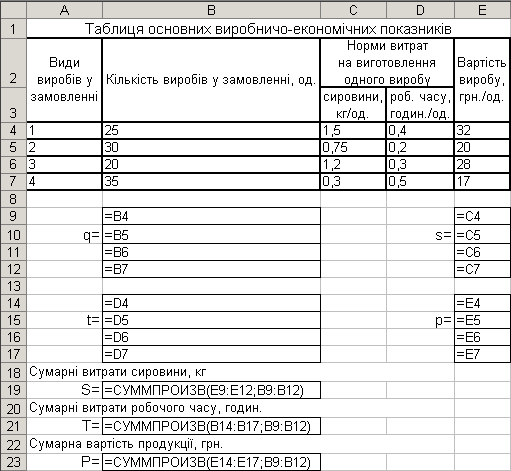
Рис.3. Вміст комірок робочого листа Excel задачі 1

Сучасні інформаційні-аналітичні системи.

Програми інвестиційного аналізу