Інформаційні системи оперативного (операційного) рівня

Інформаційна система оперативного рівня підтримує фахівців-виконавців, об­робляючи дані про угоди і події (рахунки, накладні, зарплата, кредити, потік си­ровини і матеріалів). Призначення ІС на цьому рівні — відповідати на запити про поточний стан і відслідковувати потік угод у фірмі, що відповідає оперативному керуванню. Щоб з цим справлятися, інформація повинна бути легкодоступною, безупинно діючою і бути точною. Задачі, мета і джерела інформації на опе­раційному рівні заздалегідь визначені й у високому ступені структуровані. Рішен­ня запрограмоване відповідно до заданого алгоритму.

Інформаційна система оперативного рівня є сполучною ланкою між фірмою і зовнішнім середовищем. Якщо система працює погано, то організація або не одержує інформації ззовні, або не видає інформацію. Крім того, система — це ос­новний постачальник інформації для інших типів інформаційних систем в ор­ганізації, тому що містить і оперативну, і архівну інформацію. Відключення цієї ІС привело б до необоротних негативних наслідків.

Приклад. Інформаційні системи оперативного рівня:

• бухгалтерська;

• банківських депозитів;

• обробки замовлень;

• реєстрації авіаквитків;

• виплати зарплати і т.д.

Резюме

Інформаційні системи відносяться до складних систем і орієнтовані головним чином на розв'язок різного типу задач, включаючи неструктуровані або частково (погано) структуровані задачі управління. Класифікація ІС може бути виконана за різними принципами, одним з яких є принцип структурованості задач.

Контрольні питання

1. Які ознаки класифікації інформаційних систем?

2. Чим відрізняються інформаційні системи, призначені для менеджменту, від інформаційних систем бухгалтерського обліку?

3. Що таке частково структуровані і неструктуровані задачі?

4. Назвіть типи інформаційних систем, що використовуються при рішенні частково структурованих задач

5. Які задачі є типовими в інформаційних системах фахівців, менеджерів середньої ланки ?

6. Що таке стратегічні інформаційні системи?

Сучасні комп’ютерні технології як засіб створення прикладних інформаційних систем

Економіко-математичне моделювання на основі матричної алгебри має надзвичайно важливе значення для економістів. Пояснюється це тим, що значну частину математичних моделей економічних об'єктів і процесів вдається представити в достатньо простому й компактному вигляді – в матричній формі. Завдяки цьому з’являється можливість використовувати при дослідженні таких моделей потужний апарат матричних методів. Крім того, матричний запис економічних моделей допомагає виявити подібність у структурі багатьох економічних задач, які можуть мати зовсім несхожі формулювання, а матричний аналіз економічним систем дозволяє досліджувати взаємозв'язки між об'єктами цих систем. Прикладами найпростіших матричних моделей в економіці є лінійна модель міжнародної торгівлі; модель експорту та імпорту; ціни в системі міжгалузевих зв'язків; відкрита і замкнута моделі міжгалузевого балансу тощо.

Дослідження матричних моделей в економіці за допомогою електронних таблиць Excel.

Найпростіші матричні операції в економічних розрахунках

Теоретична довідка. Матрицею називається прямокутна таблиця чисел. Загальний запис прямокутної матриці, що складається з рядків і стовпців, має вигляд

,

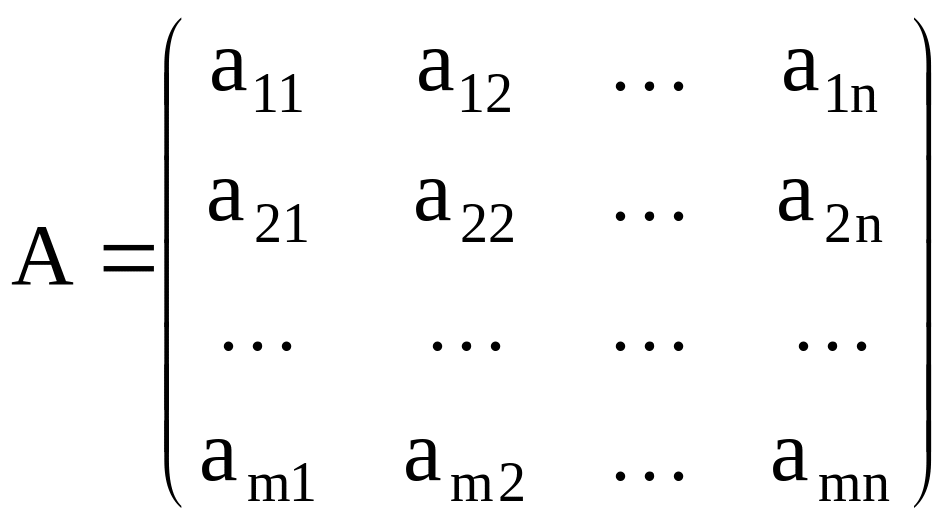де  елемент матриці, який стоїть в -му рядку і -му стовпцю ( ; ). Така матриця має розмірність . Скорочений запис цієї матриці має вигляд: .

Матриця називається квадратною матрицею -го порядку, якщо кількість рядків дорівнює кількості стовпців, тобто .

Квадратна матриця називається одиничною матрицею -го порядку, якщо її елементи визначаються за формулою: . Наприклад, наступні матриці: ; ; – одиничні матриці відповідно 1-го, 2-го і 3-го порядків.

Вектором будемо називати матрицю, що складається з одного рядка (вектор-рядок), або з одного стовпця (вектор-стовпець).

Загальний запис вектора, що складається з елементів, має вигляд:

– вектор-стовпець, – вектор-рядок. Скорочений запис цього вектора має вигляд: .

Додавання двох прямокутних матриць. Ця операція визначена лише для матриць однакової розмірності.

Якщо маємо матриці і , то сумою (різницею) двох матриць буде матриця , елементи якої визначаються за формулою: .

Множення матриці на число. Ця операція визначена для будь-яких матриці і числа.

Якщо маємо матрицю і число , то добутком матриці і числа буде матриця , елементи якої визначаються за формулою: .

Транспонування матриці. Ця операція визначена для будь-якої матриці.

Матриця називається транспонованою щодо матриці , якщо рядки матриці є стовпцями матриці , а стовпці матриці  рядками матриці .

З визначення транспонованої матриці випливає, що якщо матриця має розмірність , то транспонована матриця має розмірність .

Якщо маємо матрицю , то результатом транспонування матриці буде матриця , елементи якої визначаються за формулою: .

Для здійснення операції транспонування в Excel використовується вбудована функція ТРАНСП(масив), де масив – це діапазон комірок, де знаходиться матриця, яка підлягає транспонуванню.

Добуток двох матриць. Операція добутку двох матриць має сенс тільки в тому випадку, якщо кількість стовпців першої матриці дорівнює кількості рядків другої матриці. В результаті отримаємо таку матрицю, яка буде мати стільки рядків, скільки має перша матриця, і стільки стовпців, скільки має друга матриця.

Якщо маємо матриці і , то добутком цих двох матриць буде матриця , елементи якої визначаються за формулою:

.

Для обчислення добутку двох матриць в Excel використовується вбудована функція МУМНОЖ(масив1; масив2), де масив1 – діапазон комірок, який займає перша матриця; масив2 – діапазон комірок, який займає друга матриця.

Добуток матриці на вектор. Ця операція має сенс тільки у випадку, якщо кількість стовпців матриці дорівнює кількістю елементів вектора. В результаті отримаємо вектор, який буде мати стільки елементів, скільки рядків має матриця.

Якщо маємо матрицю і вектор , то добутком матриці на вектор буде вектор , елементи якого визначаються за формулою:

.

В Excel для обчислення добутку матриці на вектор також використовується вбудована функція МУМНОЖ(масив1; масив2), де масив1 – діапазон комірок, який займає матриця; масив2 – діапазон комірок, який займає вектор.

Скалярний добуток двох векторів. Ця операція визначена тільки для векторів, які мають однакову кількість елементів. Результатом цієї операції є число.

Якщо маємо вектори і , то скалярний добуток векторів X і Y визначається за формулою

.

В Excel для обчислення скалярного добутку двох векторів можна використовувати вбудовану функцію СУММПРОИЗВ(масив1; масив2), де масив1 – діапазон комірок, який займає перший вектор; масив2 – діапазон комірок, який займає другий вектор.

Визначник матриці. Обчислюється лише для квадратних матриць.

Для розв’язання багатьох математичних задач визначник матриці є необхідною, край важливою характеристикою.

Нагадаємо з курсу вищої математики, що визначник матриці 2-го порядку обчислюється за формулою: , а всі визначники матриць вищих порядків обчислюються поступовим зниженням порядку до другого включно з подальшим використанням формули обчислення . В загальному вигляді визначник квадратної матриці порядку можна обчислити за формулою для довільного фіксованого -го рядка, або за формулою для довільного фіксованого -го стовпця, тобто він дорівнює сумі добутків елементів будь-якого рядка (або будь-якого стовпця) матриці на їх алгебраїчні доповнення. Нагадаємо, що алгебраїчне доповнення елементу матриці задається формулою , де – визначник матриці, яку отримаємо, якщо в матриці викреслити одночасно -й рядок і -й стовпець. Визначник називається мінором елементу .

В Excel для обчислення визначника квадратної матриці використовується вбудована функція МОПРЕД(масив), де масив  це діапазон комірок, у якому зберігається матриця.

Обернення квадратної матриці. Ця операція має сенс лише для квадратних матриць, визначник яких не дорівнює нулю, тобто для невироджених матриць.

Квадратна матриця має свою обернену матрицю , якщо визначник матриця відмінний від нуля: , а також якщо виконується ланцюжок умов: , де – одинична матриця.

Обернена матриця в загальному вигляді обчислюється за допомогою відомої з курсу вищої математики формули , де матриця складається з алгебраїчних доповнень елементів , тобто .

В Excel для обчислення оберненої матриці використовується вбудована функція МОБР(масив), де масив  це діапазон комірок, у якому зберігається вхідна матриця.

Слід нагадати, що реалізація операцій транспонування матриці, множення матриць, обернення матриці за допомогою вбудованих функцій ТРАНСП( ), MУМНОЖ( ), МОБР( ) здійснюється з використанням інструменту Excel формули масиву.

Задача 1. Підприємство отримало замовлення на виготовлення з даної сировини виробів 4-х видів, основні виробничо-економічні показники для яких наведені в табл. 1. Визначити сумарну вартість продукції, що випускається підприємством, а також кількість витраченої при цьому сировини та робочого часу.

Таблиця 1

Види виробів у замовленні	Кількість виробів у замовленні, од.	Норми витрат на виготовлення одного виробу		Вартість виробу, грн./од.
		сировини, кг/од.	роб. часу, годин./од.
1	25	1,50	0,4	32
2	30	0,75	0,2	20
3	20	1,20	0,3	28
4	35	0,30	0,5	17

Рис.1. Таблиця основних виробничо-економічних показників

Розв'язання задачі

Сформуємо вектори, що утворюють табл. 1: вектор асортименту ; вектор витрат сировини на виготовлення одного виробу ; вектор витрат робочого часу на виготовлення одного виробу ; ціновий вектор :

; ; ; .

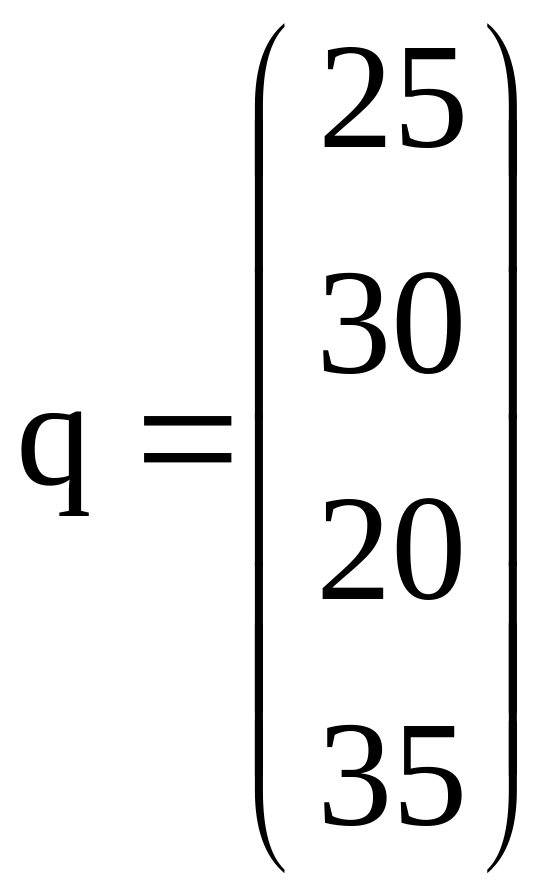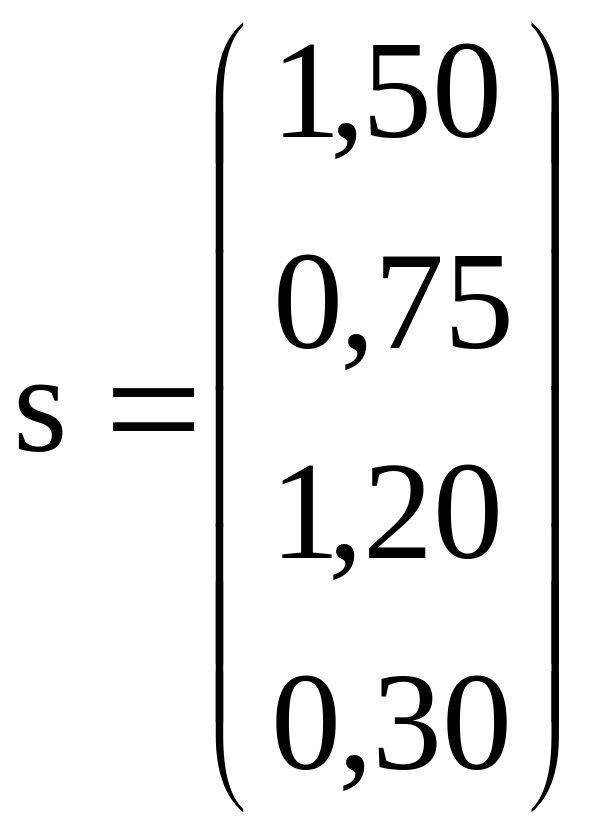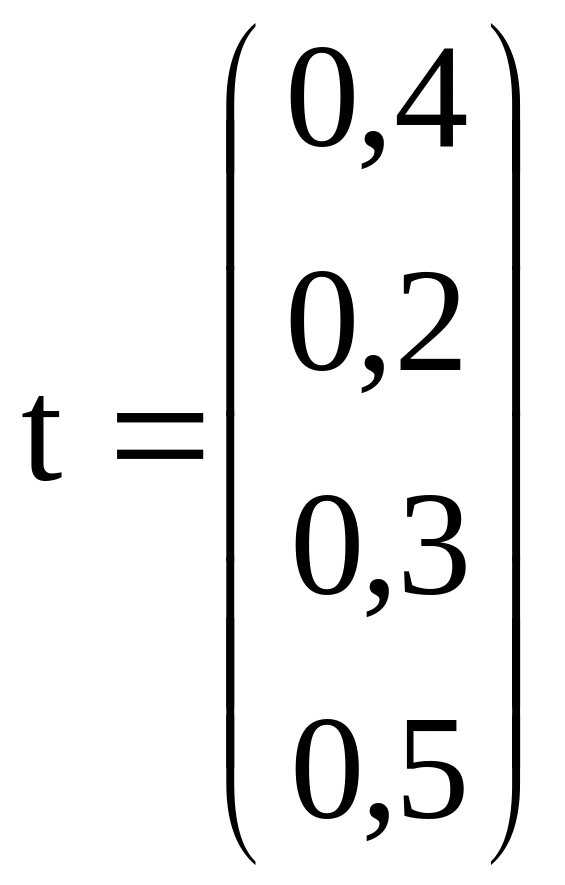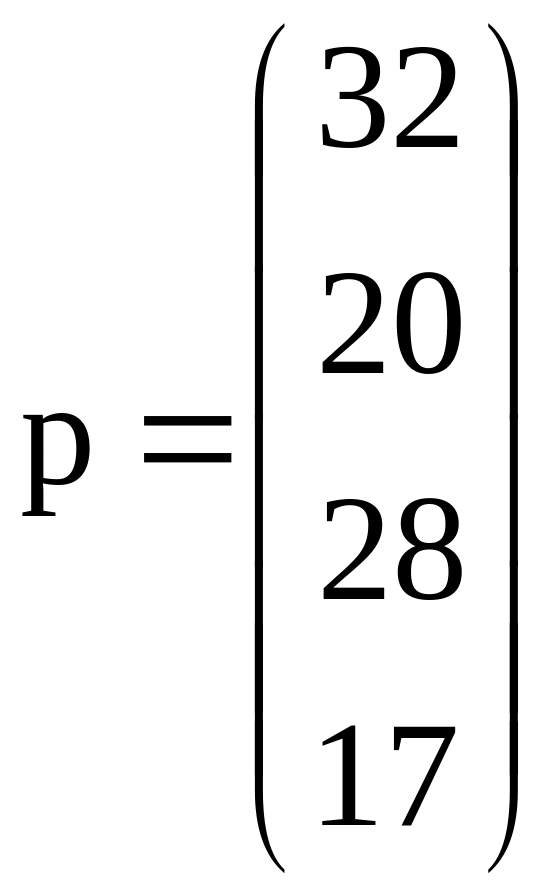Позначимо через: – сумарні витрати сировини (кг) при заданому плані випуску продукції; – сумарні витрати робочого часу (годин.); – сумарна вартість виробленої продукції (грн.).

Тоді шукані величини будуть являти собою скалярні добутки вектора асортименту відповідно на вектори , а саме: ; ; .

Переходимо до реалізації цієї задачі засобами Excel.

Дані вхідної таблиці розміщуємо у діапазоні комірок B4:E7 робочого листа Excel. Для зручності запишемо також кожний з векторів , , , в окремий діапазон комірок, а саме:

• вектор асортименту розміщуємо в діапазоні комірок B9:B12, для чого в комірку B9 заносимо формулу = B4 і копіюємо її за допомогою маркера заповнення на діапазон комірок B10:B12;

• аналогічно за цією методикою розміщуємо вектор витрат сировини , вектор витрат робочого часу і ціновий вектор відповідно в діапазонах комірок E9:E12, B14:B17, E14:E17.

Нагадаємо, що скалярний добуток двох векторів в Excel можна обчислити за допомогою вбудованої функції СУММПРОИЗВ(масив1; масив2), де масив1 і масив2 – діапазони комірок, де розташовані вектори, для яких визначається скалярний добуток.

Процес обчислення скалярних добутків при визначенні величин складається з послідовності таких кроків:

• установлюємо курсор у комірці, де буде знаходитися результат обчислень;

• активізуємо Мастер функций f_x і серед функцій категорії Математические вибираємо функцію СУММПРОИЗВ( );

• уводимо у вікні Аргументы функции діапазони комірок, в яких розташовані відповідні вектори для кожного конкретного випадку:

  • у комірці B19 обчислюємо значення величини за формулою:

=СУММПРОИЗВ(E9:E12;B9:B12);

• у комірці B21 обчислюємо значення величини за формулою:

=СУММПРОИЗВ(B14:B17;B9:B12);

• у комірці B23 обчислюємо значення величини за формулою:

=СУММПРОИЗВ(E14:E17;B9:B12);

• після кожного введення формули для одержання результату на екрані натискаємо клавішу ОК.

На рис.2 і рис.3 наведені фрагменти робочого листа Excel з отриманими результатами і вмістом комірок робочого листа.

Висновки: для виконання замовлення в повному обсязі підприємство має витратити 94,5 кг сировини та 39,5 годин робочого часу, при цьому сумарна вартість всієї виробленої продукції складатиме 2555 грн.

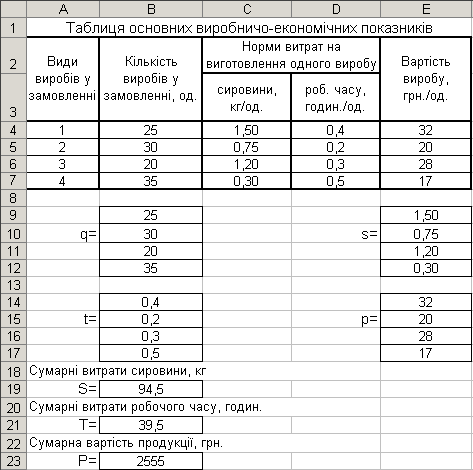
Рис.2. Робочий лист Excel з результатами розв'язку задачі 1

Інформаційні системи розв’язання балансових

задач в галузях економіки