12.2. Различные модификации уравнений массоотдачи и массопередачи

В разделе 4.4 было получено уравнение массопередачи (4.94), движущей силой в котором являлась разница химических потенциалов компонента в ядрах различных фаз. Расчет химических потенциалов представляет собой достаточно сложную задачу, о чем свидетельствует содержание предыдущего раздела. В связи с этим на практике обычно пользуются уравнениями массоотдачи и массопередачи, содержащими в качестве движущей силы разность концентраций компонента. При использовании интегральной формы уравнений массоотдачи и массопередачи (4.15), (4.109) зачастую большой проблемой является определение поверхности контакта фаз в реальном аппарате, так как она может складываться из поверхности струй, капель, пузырей, пены. В этом случае применяют модифицированные уравнения, не содержащие величину межфазной поверхности. Прежде чем приступить к выводам модифицированных уравнений массоотдачи и массопередачи получим некоторые потребующиеся при этом соотношения. Вначале рассматриваться будут двухкомпонентные смеси, а затем в разделе 12.8 – многокомпонентные.

12.2.1. Уравнения материального баланса, рабочих и равновесных линий массообменных процессов

Пусть в типичном цилиндрическом вертикальном аппарате для проведения массообменных процессов противотоком друг другу, в режиме идеального вытеснения, движутся две фазы I и II с расходами G и L, концентрацию распределяемого компонента в них обозначим y и x. Допустим, что концентрации могут изменяться только по высоте аппарата, являясь постоянными или средними для каждого поперечного сечения, т.е. упростим задачу до одномерной. Единицы измерения расходов лучше выбрать такими, чтобы G и L не изменялись по высоте аппарата (кг/с инертного компонента при абсорбции, кмоль/с смеси при ректификации и т.д.).

В стационарных условиях закон сохранения массы (вещества) для всего аппарата рис. 12.1 может быть записан в соответствии с (2.3) в виде уравнения материального баланса: суммарный приход массы (вещества) должен равняться расходу:

. (12.65)

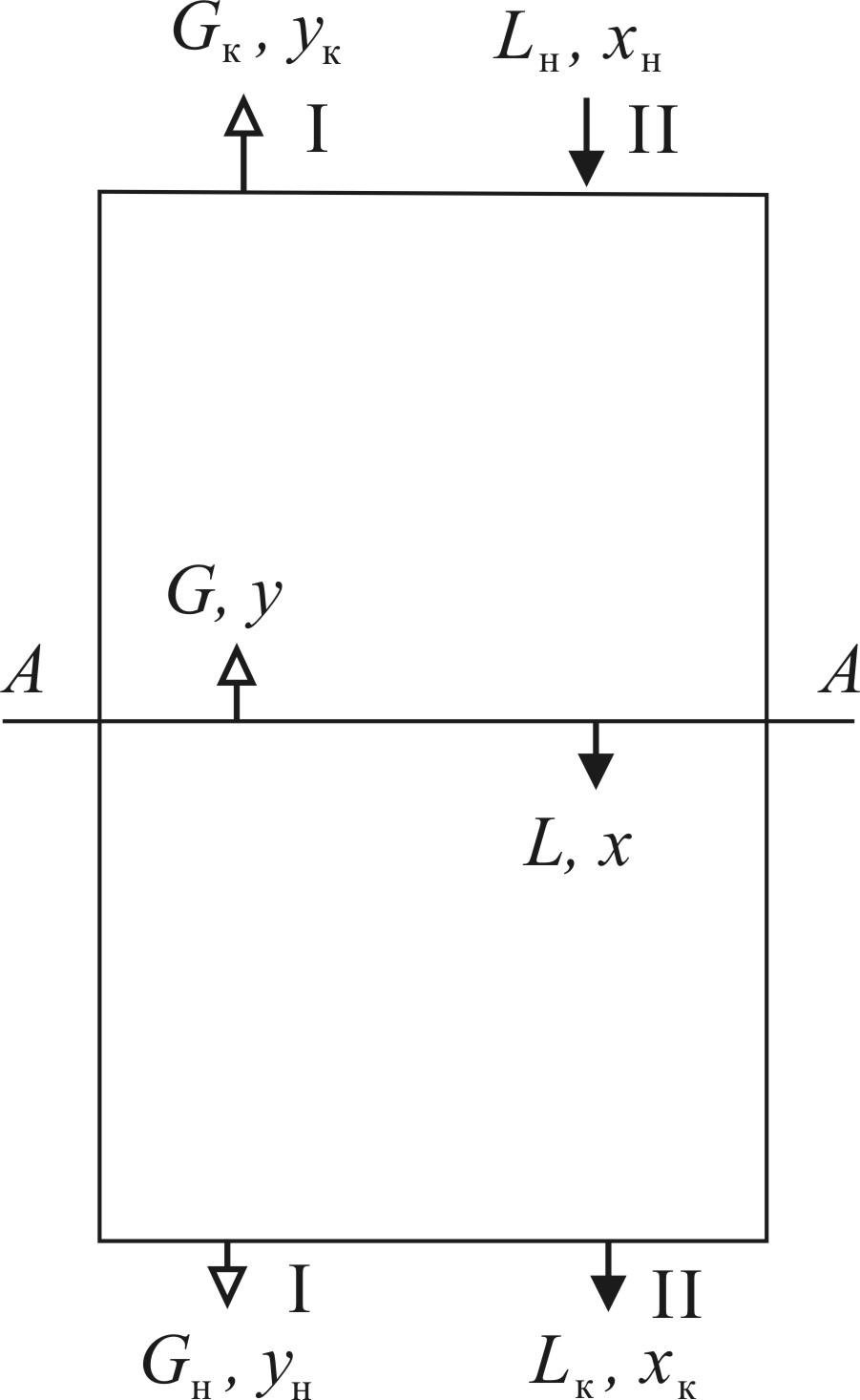
Рис. 12.1. Схема массообменного процесса в вертикальном противоточном аппарате: L, G расходы фаз; х, y концентрации распределяемого компонента в фазах; индексы «н» и «к» начальное и конечное состояния; I, II номера фаз; А  А произвольное поперечное сечение аппарата

Можно записать материальный баланс по распределяемому компоненту при отсутствии химических реакций:

. (12.66)

В случае постоянства расходов G, L=const уравнение (12.66) упрощается:

, (12.67)

или для элементарного участка аппарата

. (12.68)

Знак «минус» свидетельствует о противоположном изменении концентрации распределяемого компонента в фазах: если в одной фазе концентрация увеличивается, то в другой уменьшается.

Из уравнения материального баланса можно получить уравнение рабочей линии. Запишем уравнение материального баланса для участка аппарата от нижнего сечения до некоторого текущего А А (рис. 12.1) и разрешим его относительно концентрации распределяемого компонента в одной из фаз:

, (12.69)

. (12.70)

Это уравнение называется уравнением рабочей линии противоточного массообменного процесса, связывающего рабочие концентрации распределяемого компонента в фазах для произвольного сечения аппарата. Под рабочими концентрациями понимают средние по сечению или неизменные в сечении аппарата концентрации ядра фазы. В случае постоянства расходов уравнение рабочей линии упрощается:

. (12.71)

Это уравнение прямой линии можно представить в виде

, где , . (12.72)

Аналогичным образом может быть получено уравнение рабочей линии для прямоточного движения фаз:

, (12.73)

, (12.74)

, (12.75)

, где , . (12.76)

Запишем уравнение равновесной линии, связывающее рабочую концентрацию распределяемого компонента в одной из фаз с его равновесной концентрацией в другой фазе. Под равновесной концентрацией в произвольном сечении аппарата понимают концентрацию компонента в фазе, находящейся в равновесии с другой, состав которой определяется рабочей концентрацией. Уравнение равновесной линии может быть записано в соответствии с (12.5):

, (12.77)

где равновесная концентрация в фазе I, x рабочая концентрация в фазе II, m коэффициент распределения. Способы определения коэффициента распределения рассмотрены в предшествующем разделе. Величина m может быть постоянной (для разбавленных растворов), тогда равновесная линия будет прямой, или зависеть от x, тогда равновесная линия будет кривой.

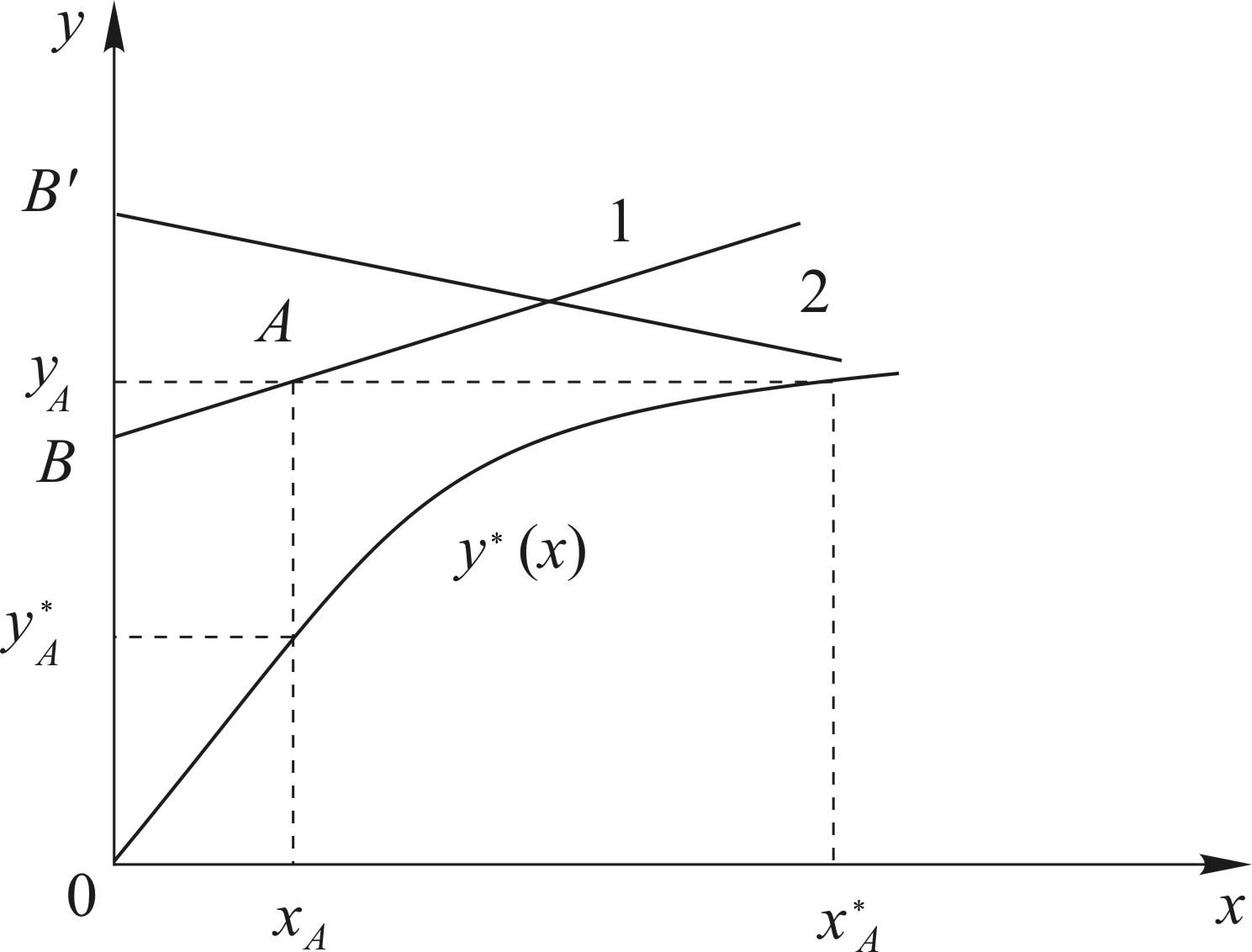
Рис. 12.2. Рабочие (1 и 2) и равновесные линии на xy диаграмме: 1 противоточное и 2 прямоточное движение фаз

На рис. 12.2 изображены рабочие и равновесные линии, причем рабочая концентрация в фазе I превышает равновесную. При стремлении системы к состоянию равновесия рабочая концентрация в каждой из фаз сближается с равновесной. Если рабочая концентрация распределяемого компонента в фазе выше равновесной, то он будет уходить из данной фазы в другую, где его концентрация ниже равновесной. В данном случае распределяемый компонент будет переходить из фазы I в фазу II, так как . В случае если рабочая концентрация компонента равна равновесной, межфазный перенос вещества отсутствует. Таким образом, по взаимному расположению рабочей и равновесной линий можно судить об отсутствии или наличии процесса массопередачи, а также о его направлении. Можно также предположить, что величина межфазного потока компонента будет пропорциональна отклонению системы от состояния равновесия, т.е. разнице рабочей и равновесной концентраций. Подтвердим данное предположение.