Глава 12. Массообмен

Основой алгоритмов проектного и поверочного расчета массообменных аппаратов является уравнение массопередачи в интегральной форме. Однако его использование в виде (4.109) затруднительно. Первая проблема заключается в нахождении средней движущей силы процесса – разности химических потенциалов компонентов в фазах. Если провести аналогию с уже изученным процессом теплопередачи, то температуры фаз могли быть замерены термометрами или найдены с применением уравнения теплового баланса. Аналогичные способы определения химических потенциалов отсутствуют. Химический потенциал компонента непосредственно измерить невозможно. Для его расчета используют соотношения между термодинамическими функциями, которые, в свою очередь, зависят от состава смеси. Поскольку концентрации компонентов могут непосредственно измеряться, например, с помощью хроматографа или ЯМР спектрометра, а также определяться из уравнения материального баланса, то на практике обычно применяются различные модификации уравнения массопередачи, в которых движущие силы выражены через концентрации. Однако движущей силой массопередачи, как это будет показано в разделе 12.2.2, является не разность концентраций компонента в фазах, а отличие концентрации компонента от равновесного значения. Таким образом, возникает необходимость определения концентраций, соответствующих условию фазового равновесия. Этот вопрос освещается в первом разделе данной главы.

Другой проблемой применения интегральной формы уравнения массопередачи является сложность определения величины межфазной поверхности во многих случаях массообмена, особенно в газожидкостных системах. Поверхностью контакта фаз в аппарате зачастую, является совокупная поверхность газовых струй и пузырей, а также пены и капель жидкости. В таких случаях используют различные модификации уравнений массопередачи, не требующие знания величины межфазной поверхности. Модифицированные уравнения массопередачи приводятся в разделе 12.2.

В данной главе по аналогии с теплообменом также рассматриваются способы нахождения полей концентраций и потоков массы, а также локальных и средних коэффициентов массоотдачи. Кроме того, приводятся классификация и схема расчета массообменных аппаратов.

12.1. Фазовые равновесия

Основная цель данного раздела установить вид зависимости между концентрациями компонентов в фазах в состоянии равновесия. Массообменные процессы химической технологии протекают в системах, состоящих из двух и более компонентов, поэтому рассматриваться будут бинарные и многокомпонентные смеси. Материал изложен с учетом достаточно подробного изучения этого вопроса в курсах физики, термодинамики и физической химии.

Условиями равновесия в гетерофазной системе, не находящейся под воздействием внешних сил, являются равенство давлений, температур и химических потенциалов компонентов во всех фазах. Химический потенциал компонента i в каждой из фаз определяют как частную производную от энергии Гиббса по числу молей i-го компонента при фиксированных давлении, температуре и количестве вещества остальных компонентов:

; . (12.1)

Определим число степеней свободы, которое можно произвольно изменять, не нарушая равновесия между фазами, иначе это количество независимых переменных, однозначно задающих состояние равновесия в гетерофазной системе. Состояние каждой из фаз определяется давлением, температурой и составом. Последний наиболее удобно выражать в мольных долях x_i. Поскольку сумма мольных долей всех n компонентов по определению равна единице, число независимых концентраций будет равно n1. Следовательно, задать состояние каждой фазы можно с помощью n1 концентрации, давления и температуры, т.е. n1+2 независимых переменных.

В условиях равновесия давление и температура во всех фазах одинаковы, а концентрации компонентов в фазах могут отличаться. С учетом этого равновесное состояние в системе из Ф фаз должно задаваться Ф(n1)+2 переменными. Однако необходимо принять во внимание равенство химических потенциалов компонентов в фазах, которое характеризуется (Ф1)n уравнениями:

. (12.2)

Поскольку химический потенциал является функцией температуры, давления и состава =(p, T, x₁, x₂, ... x_n-1), как это следует из (12.1), то уравнения (12.2) устанавливают связь между этими величинами, уменьшая количество независимых переменных на число уравнений. С учетом этого число степеней свободы С (количество независимых переменных) в равновесной гетерофазной системе будет равно

. (12.3)

Мы получили соотношение, известное как правило фаз Гиббса.

Теперь перейдем к установлению связи между концентрациями компонентов в фазах в условиях равновесия. Формальные соотношения, заменяющие (12.2), могут быть записаны чрезвычайно просто, они называются уравнениями равновесия:

, . (12.4)

Коэффициенты пропорциональности между концентрациями в условиях равновесия носят название коэффициентов распределения. Вся сложность заключается в том, чтобы их найти. Используя правило фаз Гиббса (12.3), можно определить число независимых переменных, от которых будут зависимы коэффициенты распределения. Конкретные их значения могут быть найдены из (12.4) по экспериментальным данным о равновесных концентрациях либо из (12.2), если установлен вид зависимости химических потенциалов от концентраций.

Следует отметить, что величина коэффициента распределения зависит от способа выражения концентраций в (12.4). Так, если вместо объемной мольной концентрации с_i использовать мольную долю x_i или относительную массовую концентрацию , то соответствующие коэффициенты распределения будут отличаться: . Поскольку в дальнейшем мы будем рассматривать лишь двухфазные системы, то верхние индексы у коэффициентов распределения указывать не будем. Если в каждой из фаз находится не более двух компонентов то обычно у величин не указывается и нижний индекс i, обозначающий номер компонента. При этом подразумевается, что величины относятся к распределяемому компоненту. Если границу раздела фаз пересекают оба компонента, то величины относят к легколетучему. Зачастую, чтобы не указывать номер фазы, концентрацию компонента в фазах обозначают различными буквами. Так, для обозначения мольной доли в газовой фазе обычно используют букву y, а в жидкой x. В этом случае уравнения равновесия можно записать в виде

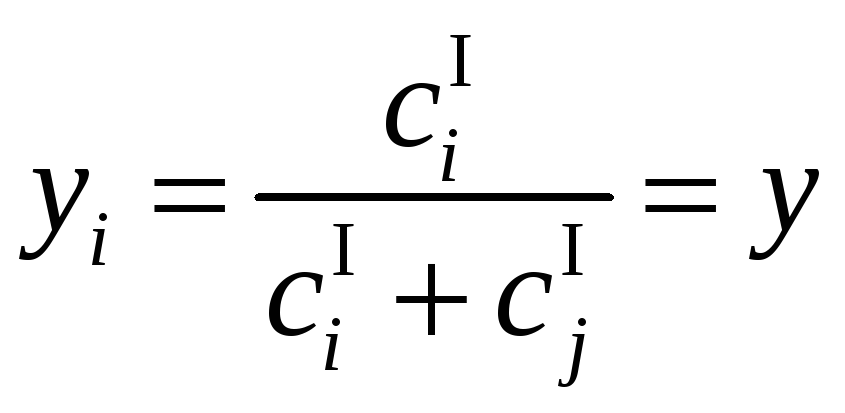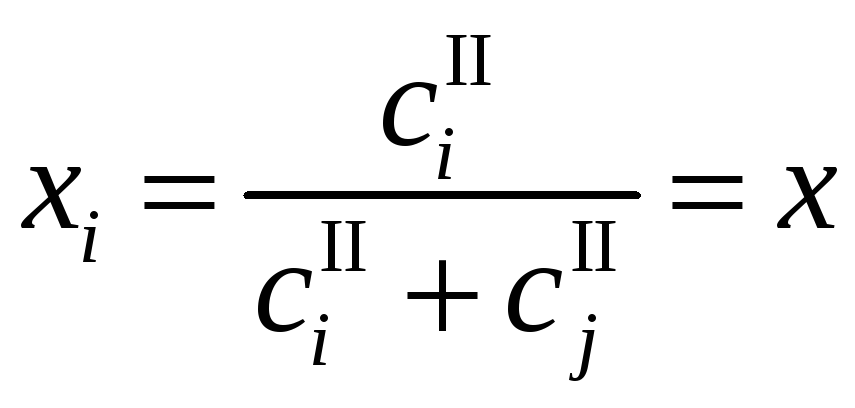, , , (12.5)

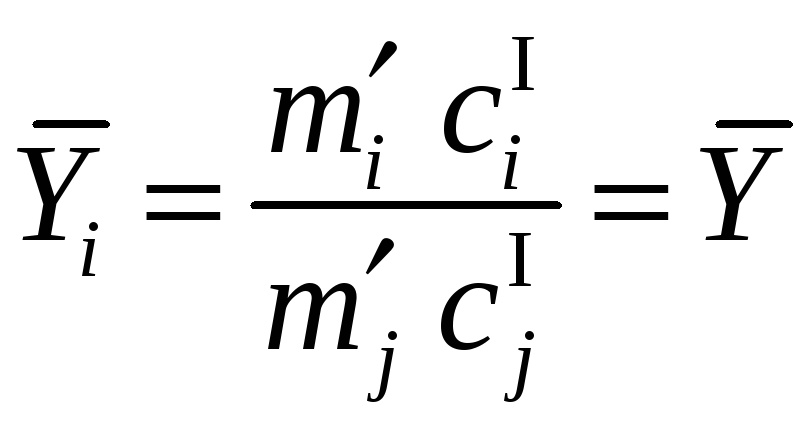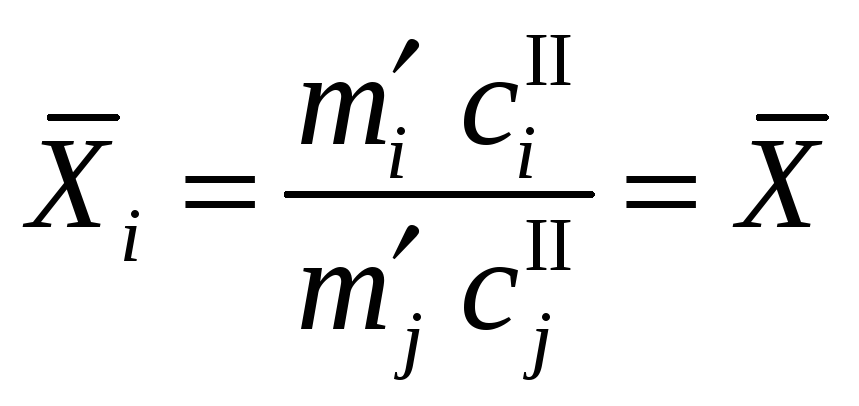, , , (12.6)

где мольная масса компонента i. Связь коэффициентов распределения при различных способах выражения концентрации приведена в [49].

Нахождение коэффициентов распределения из экспериментальных данных по равновесным концентрациям с использованием соотношений типа (12.4) (12.6) осуществляется чрезвычайно просто. Однако следует учитывать, что даже для двухкомпонентной двухфазной системы в соответствии с (12.3) С=2, коэффициент распределения будет зависеть от двух переменных. m_x=m_x(T,x)=m_x(р,x)=m_x(T,р). Следовательно, необходимо иметь набор экспериментальных данных по равновесию во всей области изменения двух параметров. При увеличении числа компонентов в системе ситуация еще более усложняется.

При отсутствии необходимого количества экспериментальных данных, а также при желании иметь аналитическую зависимость коэффициентов распределения от параметров состояния используют другой путь - устанавливают связь концентраций с химическими потенциалами, для которых условие равновесия имеет простой вид (12.2). Попытаемся такую связь установить. Льюисом было предложено записать химический потенциал в виде

, (12.7)

где некоторая функция, зависящая только от температуры, а f_i летучесть или фугитивность компонента i. Удобнее бывает использовать не абсолютную величину летучести, а относительную а_i, отнеся ее к некоторой стандартной летучести . Относительную летучесть а_i называют активностью компонента i:

, , . (12.8)

Найдем зависимость летучести от давления при постоянной температуре системы. Воспользуемся известными из термодинамики дифференциальными соотношениями:

, (12.9) . (12.10)

Тогда c учётом (12.1) получим

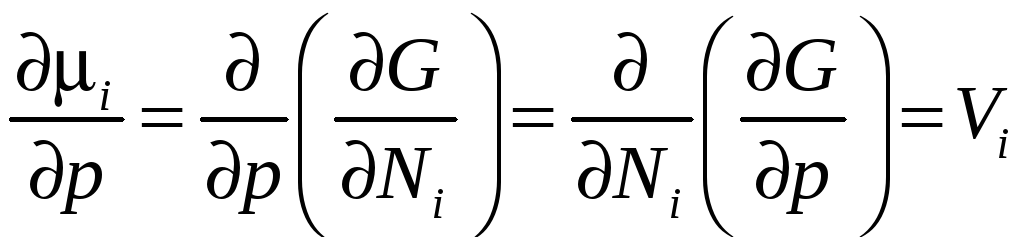, (12.11)

где V_i парциальный объем компонента i в смеси; N_i число молей компонента i.

Продифференцируем обе части уравнения (12.7) по р при Т=const с учетом (12.11):

. (12.12)

При постоянных температуре и составе смеси частная производная может быть заменена обыкновенной, так как р будет единственным аргументом:

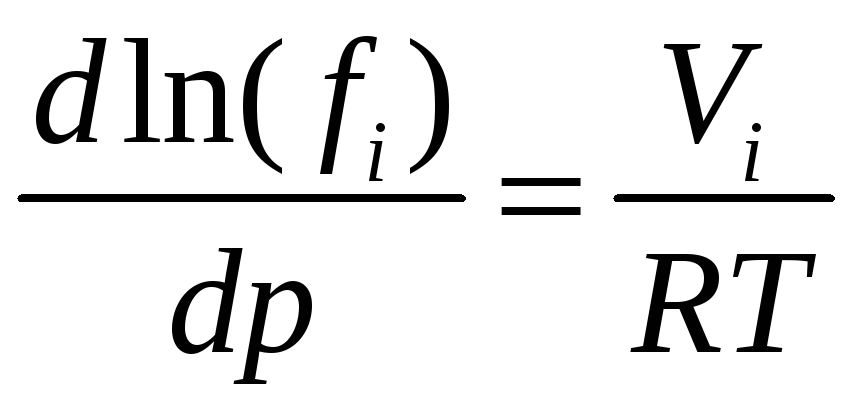, (12.13) . (12.14)

Парциальный объем компонента можно выразить через коэффициент сжимаемости z_i компонента i в смеси:

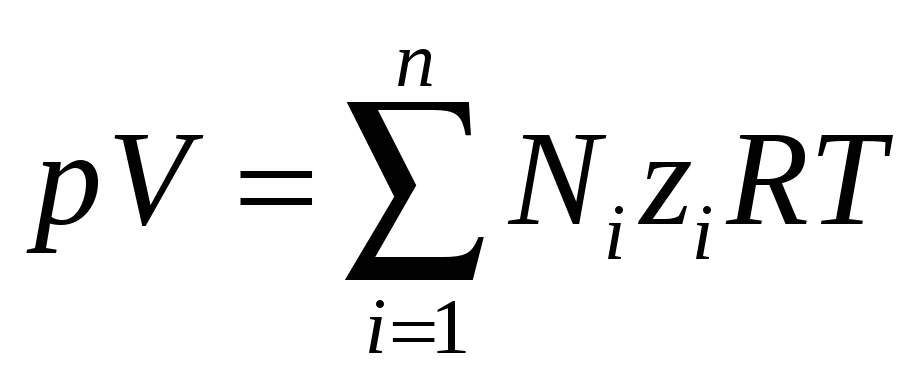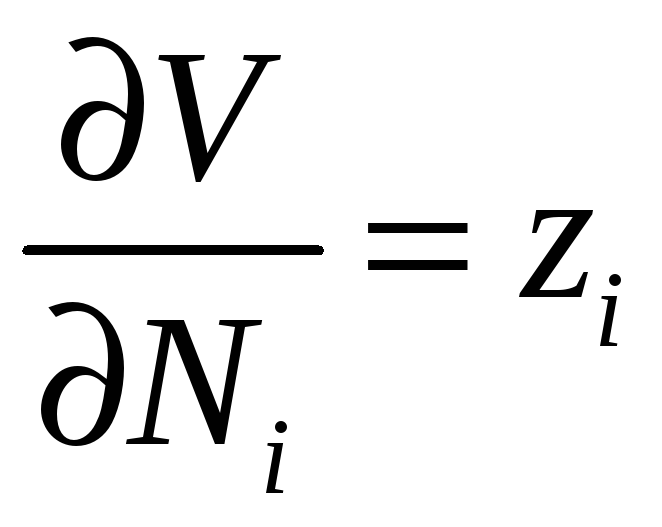
, (12.15) 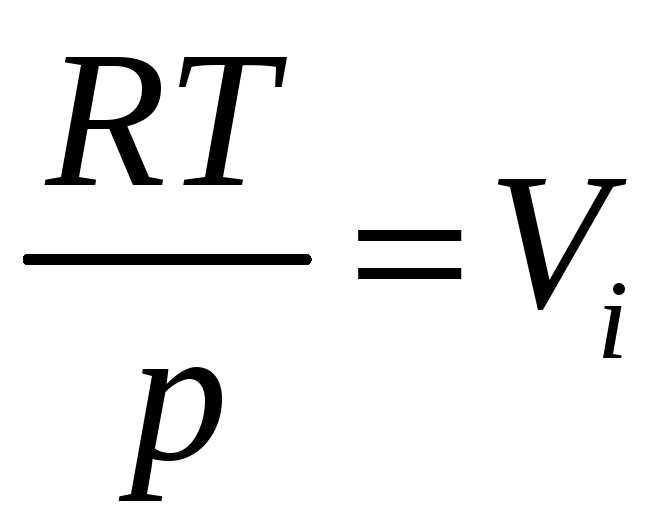, (12.16)

. (12.17)

Для определения констант интегрирования необходимо воспользоваться результатами статистической механики. Напомним, что термодинамика устанавливает лишь связи между величинами, но не позволяет найти их абсолютные значения. Рассмотрим идеальный газ модельную систему частиц, энергия взаимодействия которых пренебрежимо мала по сравнению с полной энергией системы. Статистическая механика позволяет получить для смеси идеальных газов уравнение состояния (z_i=1 в (12.15)) и равенства летучестей компонентов их парциальным давлениям:

, (12.18) . (12.19)

Используя этот результат в (12.17), можно найти :

, (12.20) 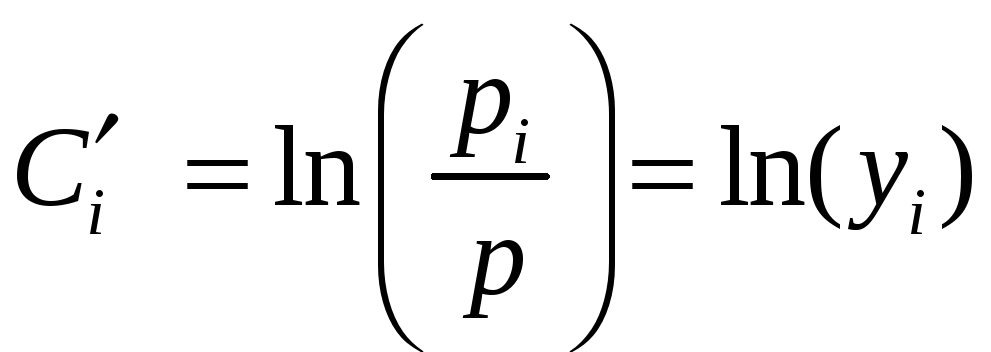. (12.21)

Отметим, что из соотношения (12.19) следует уменьшение энергии Гиббса при изобарно-изотермическом смешении чистых идеальных газов или, что эквивалентно, увеличение энтропии.

В реальных газах (парах) летучесть компонента не совпадает с парциальным давлением. Ее принято выражать через активность а_i или коэффициент летучести ф_i, выбирая в качестве стандартного состояния чистый идеальный газ сорта i при температуре и давлении реальной смеси:

, (12.22) 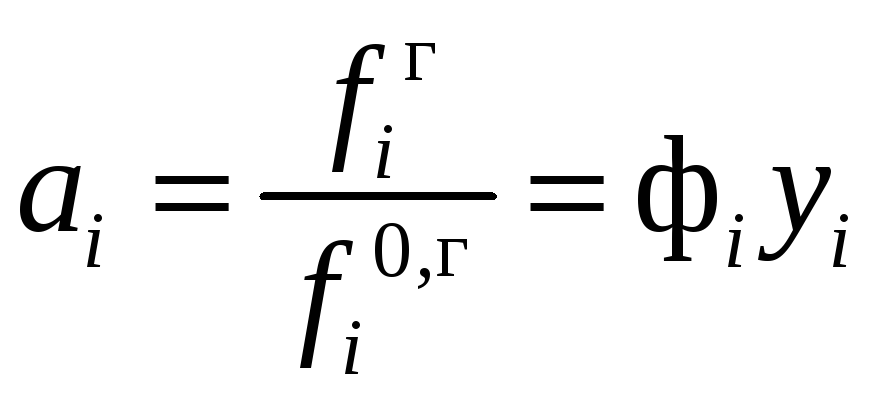, (12.23)

. (12.24)

Таким образом, задача отыскания летучести реальных газов сводится к определению коэффициента летучести ф_i.

Найдем эту величину, учитывая, что при бесконечно малом давлении реальный газ приближается к идеальному. Прибавим к правой части уравнения (12.13) и отнимем :

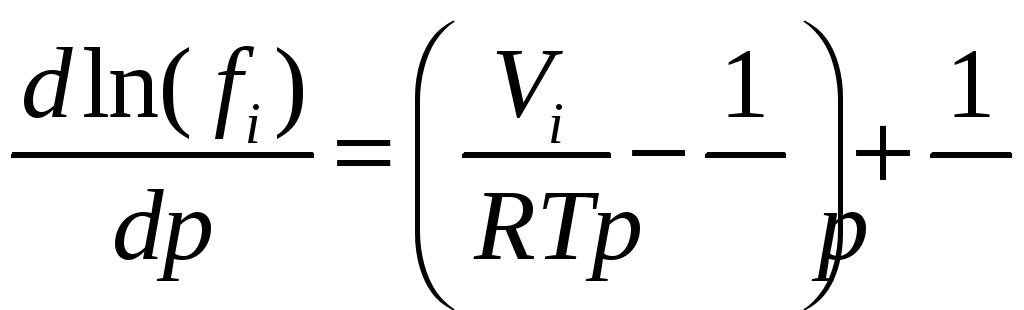, (12.25)

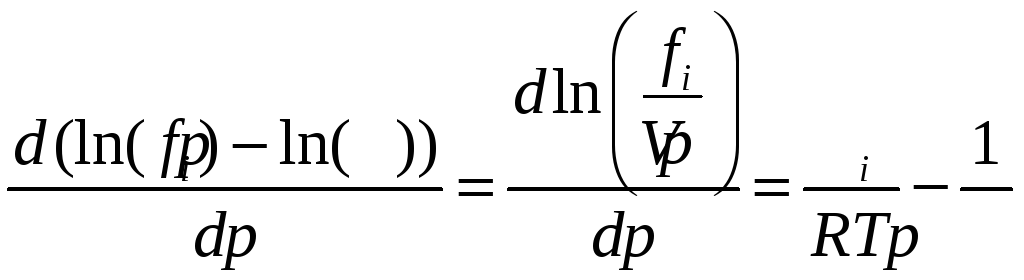. (12.26)

Проинтегрируем (12.26) по dр от 0 до р:

, (12.27)

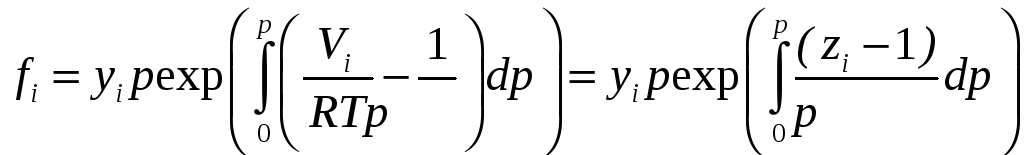, (12.28)

. (12.29)

Нетрудно убедиться, что для идеального газа (z_i=1) ф_i = 1 по (12.29), а = p_i по (12.28). В реальном газе . Для расчета летучести реального газа необходимо знание уравнения состояния, т.е. зависимости z_i(p). При этом можно использовать как теоретические, полученные с помощью методов статистической механики, так и эмпирические уравнения состояния.

При рассмотрении жидких смесей принято использовать два различных стандартных состояния. Если при температуре и давлении смеси чистый компонент i будет находиться в жидком состоянии, то именно оно выбирается в качестве стандартного. Если же при температуре и давлении смеси чистый компонент находится в газовом или твердом состоянии, то для него в качестве стандартного выбирается бесконечно разбавленное состояние:

, (12.30) 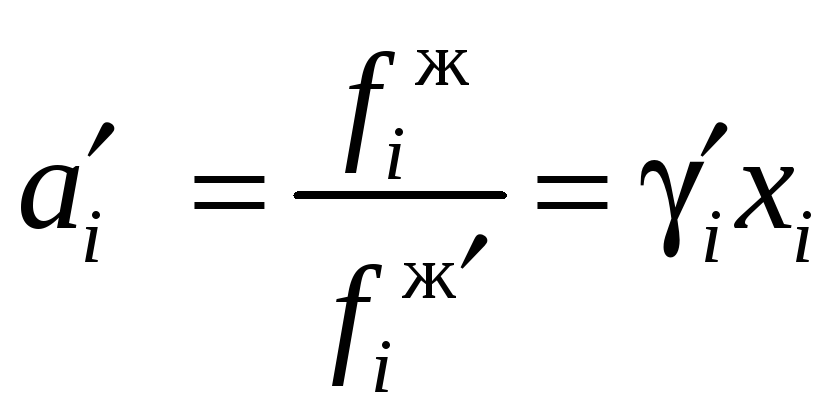, (12.31)

, (12.32) , (12.33)

, (12.34) 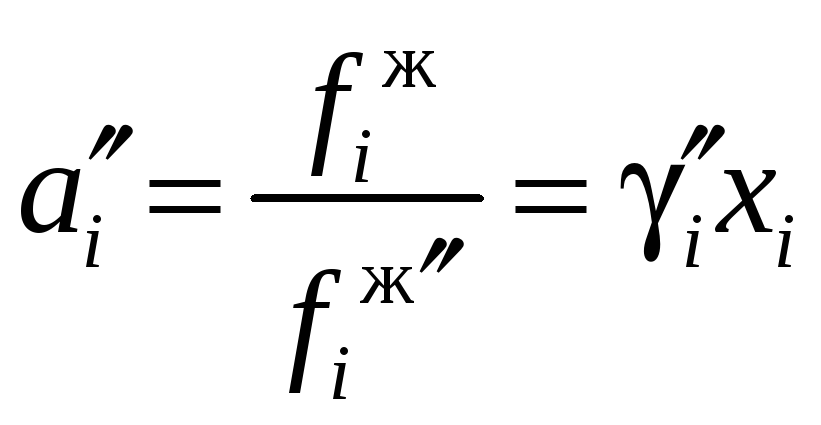, (12.35)

, (12.36) . (12.37)

Здесь и в дальнейшем штрихом обозначаются величины, характеризующие чистый компонент i (x_i  1), двумя штрихами бесконечное разбавление (x_i  0), за исключением активностей а_i и коэффициентов активности _i , для которых штрихи указывают лишь на выбор первого или второго стандартного состояния.

Для определения коэффициентов активности воспользуемся соотношением (12.28), справедливым для любого фазового состояния. Прибавим и отнимем под интегралом коэффициент сжимаемости z_i чистого компонента i при выборе первого стандартного состояния:

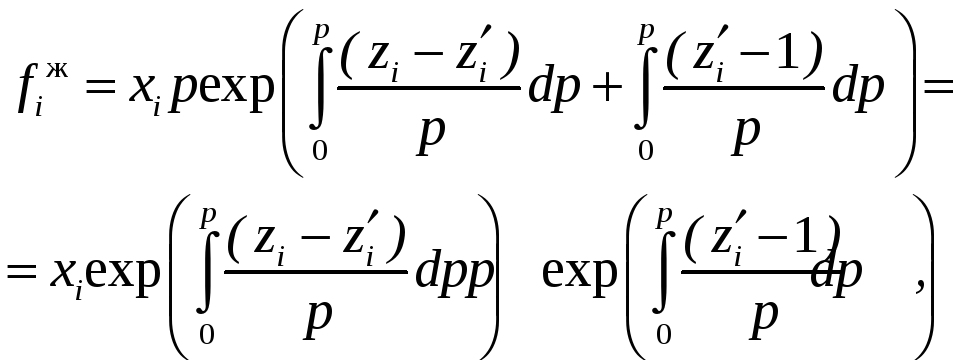(12.38)

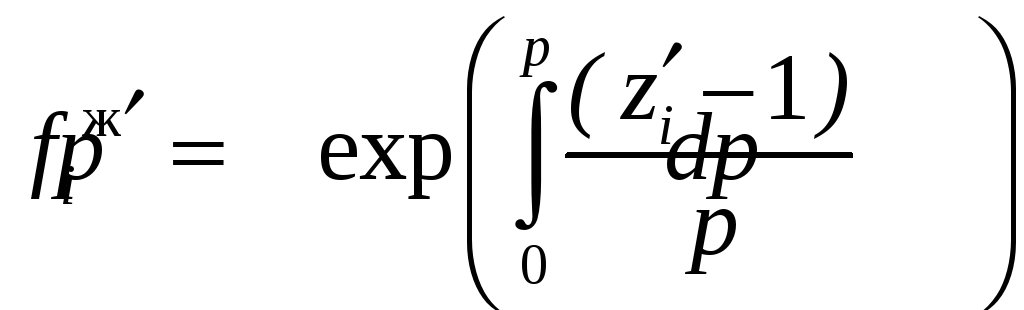. (12.39)

Сопоставив (12.38) с (12.32), найдем _i:

. (12.40)

Аналогичным образом можно определить коэффициент активности и для второго стандартного состояния:

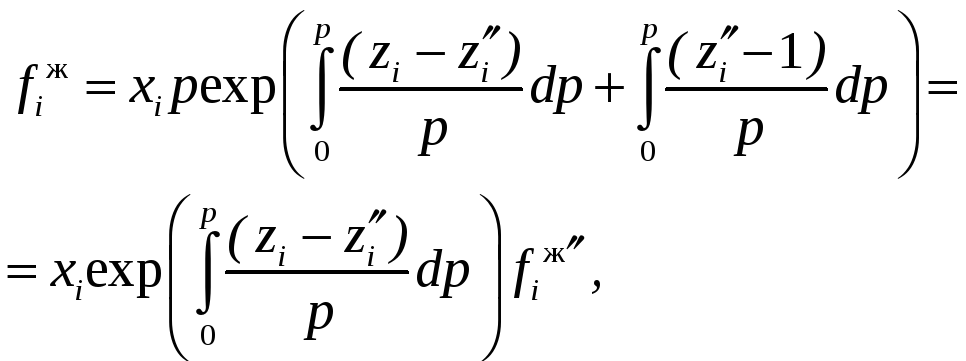(12.41)

, (12.42) . (12.43)

Необходимо учитывать, что интегрирование по dр в соотношениях (12.38)(12.43) проводится при малых р в газовой области, а при давлении больше равновесного в жидкой. Это требует знания уравнений состояния смеси в газовой и жидкой фазах. Из (12.40) (12.43) видно, что коэффициенты активности будут равны единице, если коэффициент сжимаемости компонента i в смеси или парциальный объем V_i не отличается от его значения в стандартном состоянии. Такие смеси называются идеальными. Не следует путать идеальную смесь с идеальным газом, для которого коэффициенты летучести ф_i=1 и сжимаемости z_i=1 равны единице.

Используя летучесть, можно по-иному сформулировать условие фазового равновесия (12.2). Учитывая равенство температур в фазах, а следовательно, и _i⁺, из (12.2) и (12.7) получим

. (12.44)

Найдем теперь коэффициенты распределения m_i для различных случаев равновесия в двухфазных системах.

Равновесие в системе пар – жидкость. Условие равновесия будет иметь вид

или , (12.45)

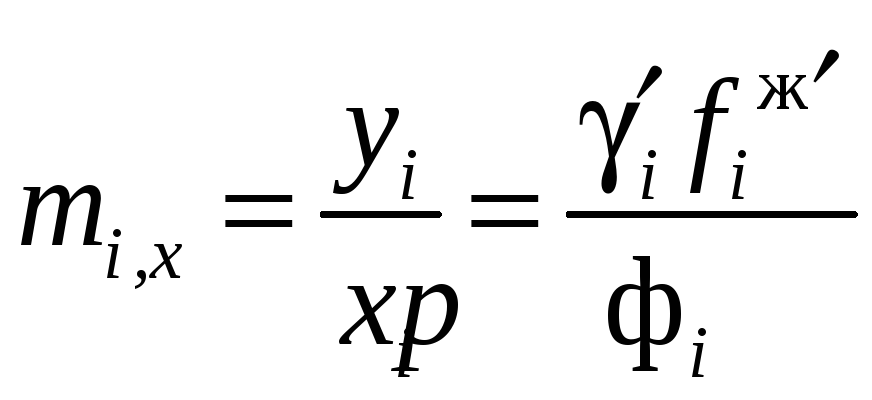. (12.46)

Имея уравнения состояния рассматриваемой смеси в паровой и жидкой фазах. по соотношениям (12.29), (12.39), (12.40), (12.46) можно определить коэффициенты распределения для всех компонентов. Однако необходимо иметь в виду, что в двухфазной системе, в соответствии с правилом фаз Гиббса, число степеней свободы соответствует числу компонентов. Поэтому задав, например, состав жидкой фазы (n1) мольной долей x_i и температуру T, мы уже не можем произвольно задать давление р. Оно будет определяться условиями равновесия. Это затрудняет расчет коэффициентов распределения по предложенным соотношениям. Задачу приходится решать, как правило, методом последовательных приближений, определяя р из соотношения

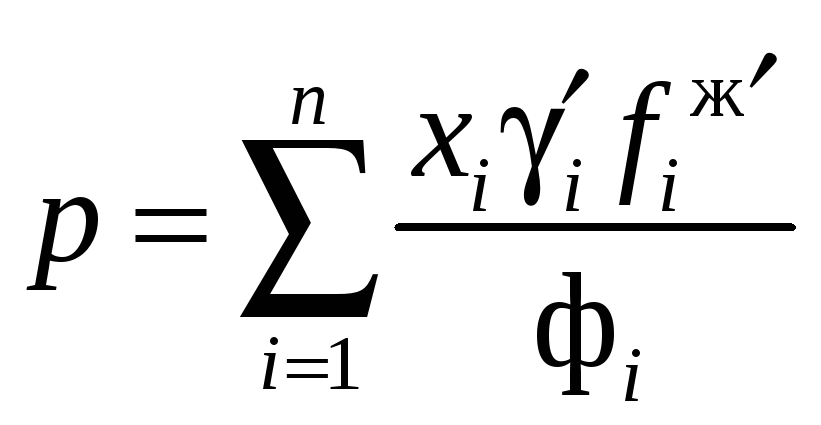, (12.47)

либо непосредственно решать численными методами систему уравнений (12.29), (12.39), (12.40), (12.45), (12.46).

Вместо подставим выражение (12.39), интеграл в котором разделим на две части. Проведем интегрирование от нуля до давления насыщенного пара чистого компонента i при температуре смеси, а затем от до давления смеси р и выполним ряд математических преобразований.

Проведем некоторые полезные для практического использования упрощения:

(12.48)

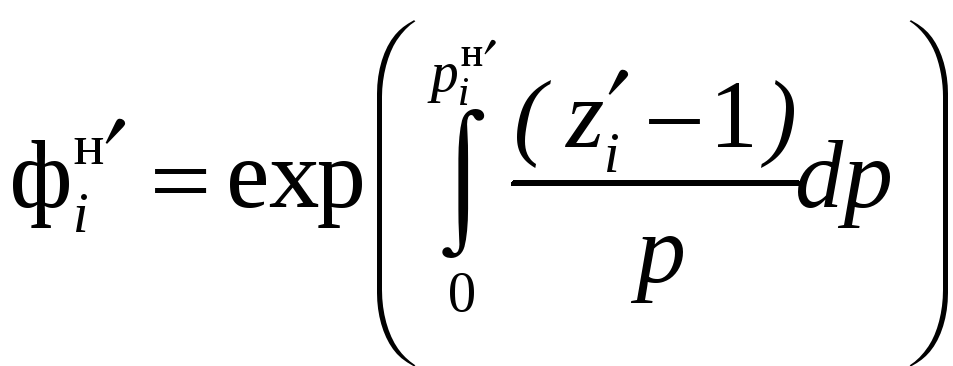. (12.49)

Подставив (12.48) в (12.46), получим

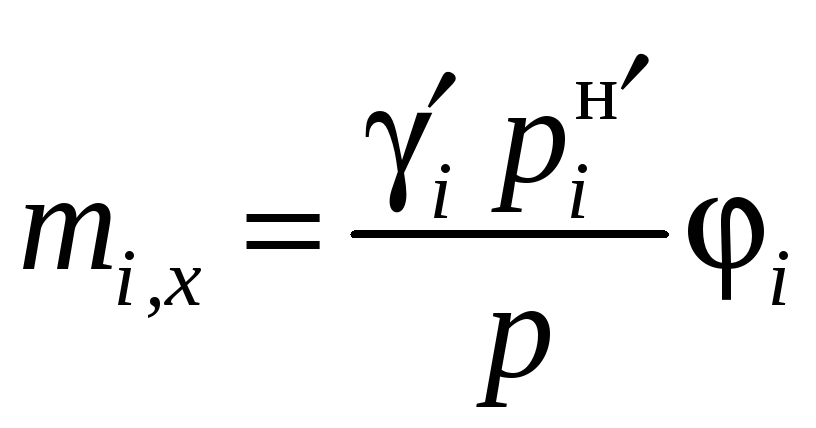, (12.50) . (12.51)

Для умеренных давлений величина _i близка к единице, что позволяет приближенно рассчитывать коэффициенты распределения и давление без учета _i:

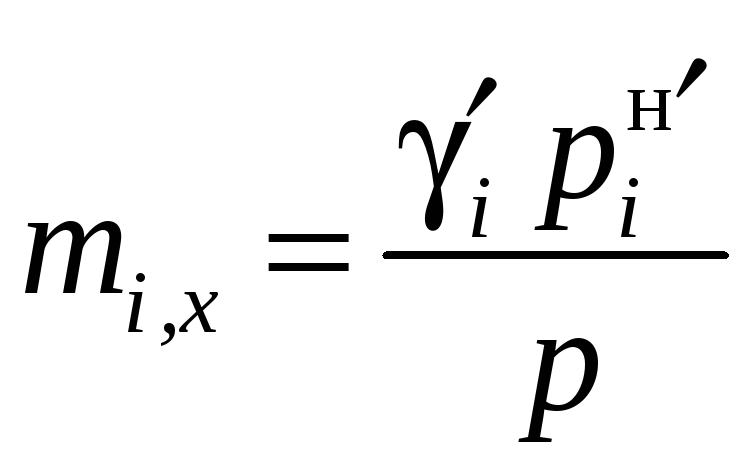, (12.52)

Если жидкая смесь является идеальной, _i = 1 и

или . (12.53)

Соотношение (12.53) является выражением так называемого закона Рауля, справедливого для идеальных смесей, и позволяет определять коэффициенты распределения без итерационных процедур, так как проведенные упрощения приводят к простому выражению для давления смеси:

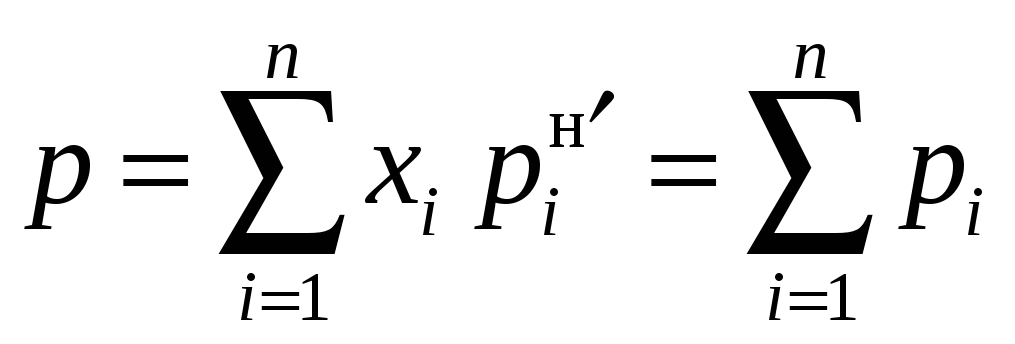. (12.54)

Равновесие в системе газ – жидкость. Для компонентов, обладающих критической температурой ниже температуры смеси, воспользоваться соотношениями (12.50) или (12.53) не представляется возможным, так как при температуре смеси для чистого компонента i не существует давления, при котором газ конденсировался бы, т.е. для такого компонента понятие «давление насыщенного пара» (находящегося в равновесии с жидкостью) р_i^н не имеет смысла. В этом случае обычно используют второе стандартное состояние бесконечно разбавленный раствор данного компонента в жидкой фазе. Условие равновесия будет иметь вид

или , (12.55)

. (12.56)

Совместное использование соотношений (12.29), (12.42), (12.43), (12.55), (12.56) для газовых компонентов системы количеством и (12.39), (12.46), (12.45) для паровых, позволяет строго определить коэффициенты распределения. В случае малых концентраций газового компонента i в жидкой смеси ее можно считать идеальной = 1, для невысоких давлений ф_i = 1 и выражение для m_i,x упрощается:

, (12.57) 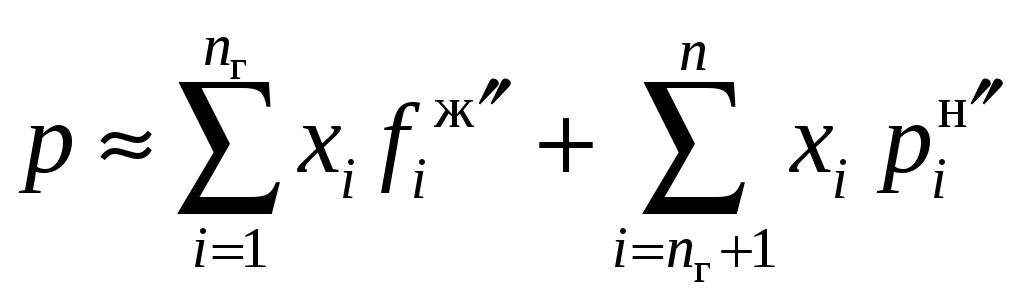. (12.58)

Для бинарной смеси (12.57) приобретает вид, называемый законом Генри:

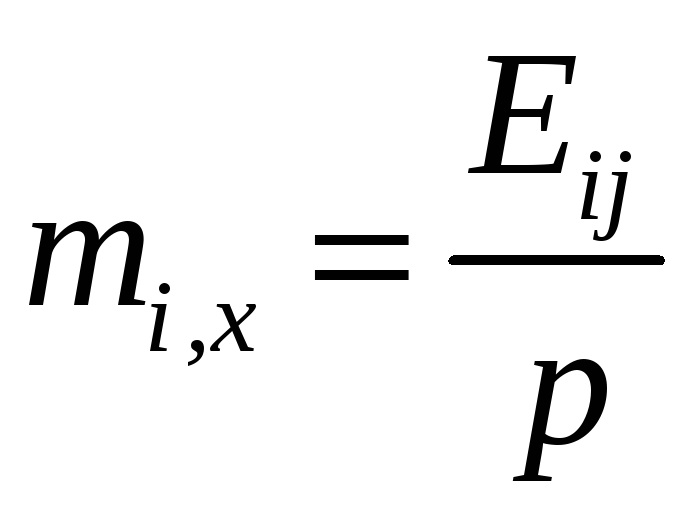или , (12.59)

где Е_ij коэффициент Генри, существенно зависящий от температуры и характеризующий растворимость i-го газа в j-й жидкости. Значения коэффициентов Генри для различных систем и их зависимости от температуры приводятся в справочной литературе. Если газ i растворяется в смеси компонентов, то в первом приближении может быть найдена с использованием коэффициентов Генри следующим образом:

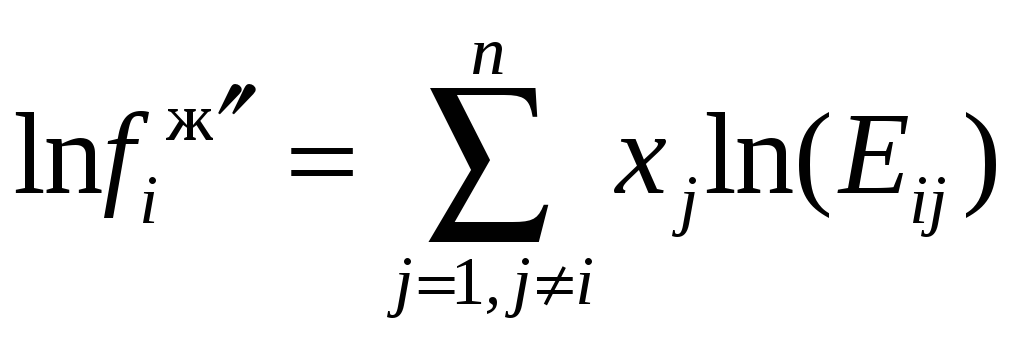. (12.60)

Соотношения (12.55) (12.60) могут применяться не только для газовых, но и для паровых компонентов, особенно если они присутствуют в небольшом количестве в неидеальной жидкой смеси.

Равновесие в системе жидкость – жидкость. Ряд жидкостей обладает ограниченной растворимостью, что приводит к расслоению системы на фазы, например, керосин вода. Расслаиваться могут только сильно неидеальные смеси, у которых энергия притяжения разнородных молекул значительно меньше, чем у однородных. Расслоение может иногда наблюдаться лишь в определенной области температур и концентраций, а за ее пределами система будет однофазной. Давление оказывает незначительное влияние на равновесие в системе жидкость жидкость. Условие равновесия в двухфазной жидкой системе имеет вид

или , (12.61)

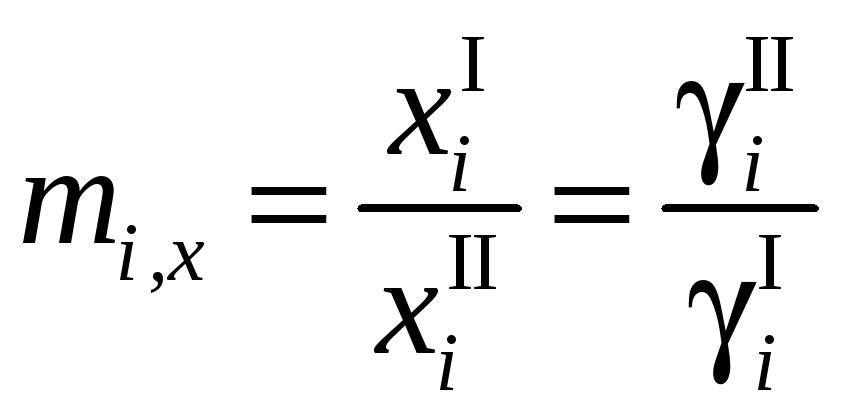. (12.62)

Таким образом, нахождение коэффициента распределения сводится к расчету коэффициентов активности компонента i в различных фазах.

Определение коэффициентов активности представляет сложную задачу ввиду отсутствия надежных уравнений состояния неидеальных жидких смесей, необходимых для (12.40). На практике часто используют модельные уравнения, описывающие отклонение жидкой смеси от идеальной. Они основаны на различных моделях определения избыточной по отношению к идеальной смеси энергии Гиббса и позволяют рассчитать коэффициенты активности с использованием нескольких параметров для каждой пары компонентов, составляющих смесь. Эти параметры извлекаются из экспериментальных данных по фазовому равновесию бинарных систем и приведены в справочной литературе. Наиболее универсальным является единое квазихимическое уравнение ЮНИКВАК, кроме того, широко используются более простые уравнения Вильсона и НРТЛ. Для смесей веществ, для которых отсутствуют какие-либо экспериментальные равновесные данные, возможен прогнозный расчет коэффициентов активности с помощью уравнения ЮНИФАК. Оно базируется на уравнении ЮНИКВАК и методе групповых составляющих, суть которого заключается в определении свойств вещества по составляющим его структурным группам (метильная, карбонильная и т.д.) [46].

Равновесие в системе твердое тело – жидкость. Рассмотрим простейший случай, когда твердое тело представляет собой чистый компонент i. Условие равновесия его со смесью жидких компонентов будет иметь вид

или . (12.63)

Использование коэффициента распределения в этом случае не имеет смысла, так как мольная доля компонента i в твердой фазе известна (равна единице). Величиной, подлежащей определению, является равновесная концентрация компонента i в жидкой фазе, называемая концентрацией насыщения, или растворимостью:

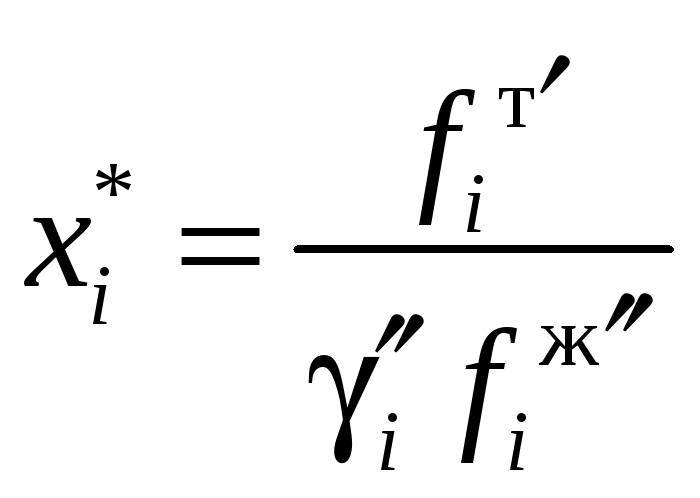. (12.64)

В частном случае двухкомпонентной двухфазной системы число степеней свободы равно двум. Учитывая малую зависимость свойств конденсированных сред от давления, можно считать единственной величиной, определяющей растворимость твердого вещества в однокомпонентном растворителе, температуру. Растворимости твердых веществ в различных растворителях при определенных температурах приводятся в справочной литературе.