12.7.3. Специфика расчета аппарата со ступенчатым контактом фаз

Основная особенность аппаратов со ступенчатым контактом фаз заключается в существенной дискретной неоднородности удельной поверхности контакта фаз по высоте аппарата. Кроме того, в большинстве случаев для них неприемлемо допущение о параллельном движении фаз в режиме идеального вытеснения, которое использовалось при выводе основного уравнения массопередачи.

Рассмотрим схему проектного технологического расчета массообменного аппарата со ступенчатым контактом фаз на примере тарельчатой колонны с противоточным движением газовой и жидкой фаз, наиболее широко применяемой в промышленности (рис. 12.7). Сохраним постановку задачи, сформулированную в предыдущем разделе. Расход жидкой фазы L, конечная концентрация распределяемого компонента в ней x_к, диаметр аппарата D и скорости движения фаз определяются в соответствии с первым и вторым этапами расчета аппаратов с непрерывным контактом фаз.

Высоту колонны можно связать с числом тарелок N и межтарельчатым расстоянием h_м:

. (12.213)

Величина h_м, являясь одним из параметров оптимизации, в первом приближении может определяться из условия максимально допустимого уноса капель жидкости газовым потоком. Для различных типов тарелок имеются соотношения, связывающие величину уноса е с межтарельчатым расстоянием h_м, скоростью газовой фазы W_y⁰, теплофизическими свойствами газовой и жидкой фаз. Обычно допускают е 0,1 кг жидкости / кг газа.

О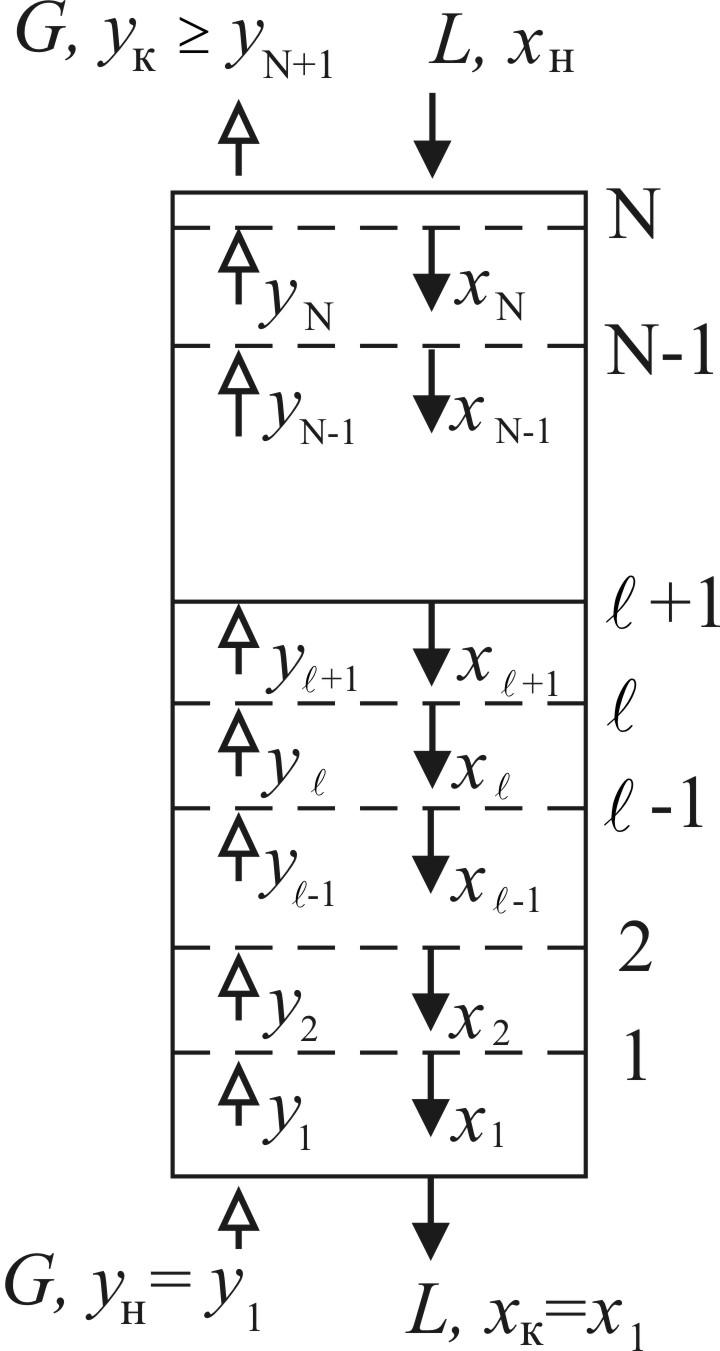сновной задачей технологического расчета тарельчатой колонны является определение числа тарелок N, обеспечивающих необходимый перенос распределяемого компонента из одной фазы в другую. Для этого вводится понятие эффективности тарелки по Мэрфри (к.п.д. тарелки) , характеризующее степень достижения равновесия между уходящими с тарелки фазами. Математическим определением этой величины с учетом обозначений, приведенных на рис. 12.9, является (12.214):

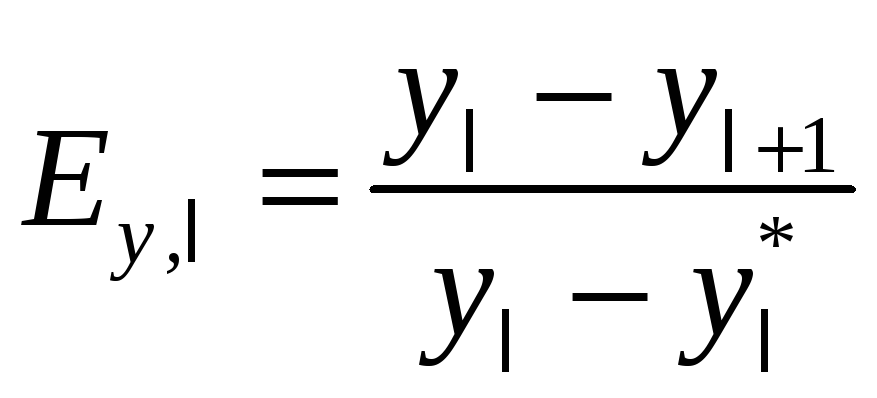, (12.214)

где концентрация распределяемого компонента в газовой фазе, равновесная с уходящим с -й тарелки потоком жидкости.

Рис. 12.9. Изменение концентраций фаз по высоте тарельчатой колонны

Аналогичным образом можно определить , используя концентрации жидкой фазы. Если = 1, то такую тарелку называют теоретической. Таким образом, теоретической тарелкой (теоретической ступенью изменения концентрации) называют участок аппарата, обеспечивающий выполнение равновесных соотношений между покидающими его составами фаз . Следует отметить, что при этом составы фаз рассматриваются в различных сечениях аппарата ( над -й тарелкой, под ней). Таким образом, в любом поперечном сечении аппарата равновесие не достигается , иначе отсутствовала бы движущая сила массопередачи. Вначале рассмотрим различные способы определения числа тарелок N, необходимого для нахождения высоты аппарата H по (12.213), а затем более подробно остановимся на расчете эффективности по Мэрфри, зависящей от коэффициентов массопередачи, межфазной поверхности, уноса и структуры потоков на тарелке.

Потарелочный расчет колонны. Этот аналитический способ определения числа тарелок основан на решении уравнений материального баланса, равновесия и использовании эффективности по Мэрфри для каждой тарелки. Для нижней тарелки под номером 1 (рис. 12.9) составы фаз известны y₁ = y_н, x₁ = x_к. Последовательно решая уравнения равновесия, (12.214) и рабочей линии, можно определить составы фаз для тарелки номер 2, затем номер 3 и т.д.

, (12.215)

, (12.216)

, (12.217)

. . . . . . . . . . . . . . . . . . . .

, (12.218)

, (12.219)

. (12.220)

. . . . . . . . . . . . . . . . . . . . .

Расчет заканчивается при значении , для которого начинает выполняться условие , при этом число тарелок N = . Следует отметить, что для аппаратов со ступенчатым контактом фаз рабочая линия приобретает дискретный характер и говорить о связи рабочих концентраций фаз имеет смысл лишь для определенных сечений аппарата, например, непосредственно под каждой тарелкой (12.217), (12.220). Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм имеет смысл реализовать на компьютере.

Для ориентировочных расчетов, выполняемых вручную, используют упрощенные графические способы нахождения числа тарелок.

Определение числа тарелок с помощью кинетической кривой. Упрощение по сравнению с предыдущим способом заключается в следующем: эффективности по Мэрфри рассчитываются не для каждой тарелки, а лишь для нескольких сечений колонны; аналитическое решение уравнений (12.215)-(12.220) заменяется графическим. Алгоритм действий следующий:

а) на ху диаграмме строятся рабочая и равновесная линии (рис. 12.10);

б) для нескольких сечений аппарата (нескольких рабочих концентраций x, y, x, y, x, y... рассчитываются эффективности тарелки по Мэрфри ;

в) находятся величины

, (12.221)

. . . . . . . . . . . . . . . . . . . . . . . .

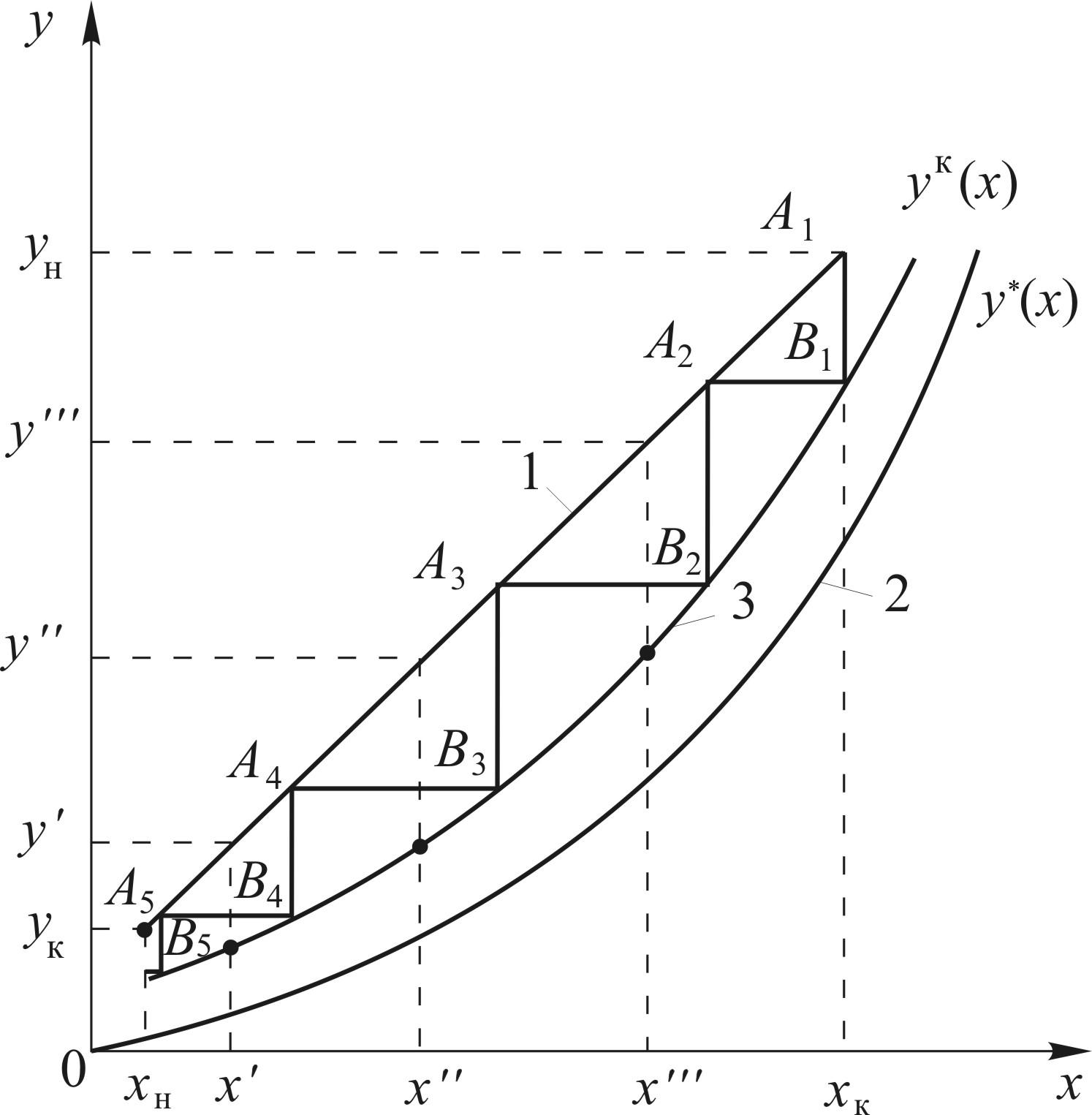
Рис. 12.10. Определение числа тарелок с помощью кинетической кривой: 1 – рабочая линия; 2 – равновесная линия; 3 – кинетическая кривая

г) на ху диаграмме наносятся точки с координатами x, y^к; x, y^к; x, y^к;... и соединяются линией, называемой кинетической кривой. Если все E_y< 1, то кинетическая кривая располагается между рабочей и равновесной линиями; если все E_y = 1, то кинетическая кривая, как следует из (12.221), совпадает с равновесной линией;

д) из точки А₁ с координатами x₁ = x_к, y₁ = y_н проводится линия, параллельная оси y, до пересечения с кинетической кривой. Находится ордината точки В₁(x₁, y₂), т.е. графическим способом решается уравнение (12.216). Из точки В₁ проводится прямая, параллельная оси x, до пересечения с рабочей линией; находится абсцисса точки А₂(x₂, y₂), т.е. графически решается уравнение (12.217);

е) процедура пункта д) повторяется для точки А₂, затем А₃ и т.д. до тех пор, пока для ординаты точки не выполнится условие . На этом построения заканчиваются, необходимое число тарелок в колонне N = .

Таким образом, аналитическое решение уравнений (12.215) (12.220), составляющих алгоритм потарелочного расчета, заменяется графическим вписыванием и определением количества прямоугольных ступеней между рабочей линией и кинетической кривой в заданном интервале изменения рабочих концентраций.